шаг

Системный объект: поэтапный. SumDifferenceMonopulseTracker2D
Пакет: поэтапный

Выполнять моноимпульсное отслеживание с помощью URA

Синтаксис

ESTANG = step(H,X,STANG)

Описание

Примечание

Начиная с R2016b, вместо использования step для выполнения операции, определенной системным object™, можно вызвать объект с аргументами, как если бы это была функция. Например, y = step(obj,x) и y = obj(x) выполнять эквивалентные операции.

ESTANG = step(H,X,STANG) оценивает входящее направление ESTANG входного сигнала, X, основываясь на начальной догадке направления.

Примечание

Объект выполняет инициализацию при первом выполнении объекта. Эта инициализация блокирует неперестраиваемые свойства и входные спецификации, такие как размеры, сложность и тип данных входных данных. При изменении неперестраиваемого свойства или входной спецификации системный объект выдает ошибку. Чтобы изменить неперестраиваемые свойства или входные данные, необходимо сначала вызвать release метод разблокирования объекта.

Входные аргументы

H

Объект трекера типа phased.SumDifferenceMonopulseTracker2D.

X

Входной сигнал, определяемый как вектор строки, число столбцов которого соответствует количеству каналов. Этот аргумент можно указать как одинарную или двойную точность.

Размер первого размера входной матрицы может изменяться для моделирования изменения длины сигнала. Изменение размера может происходить, например, в случае формы импульса с переменной частотой повторения импульса.

STANG

Начальное угадывание направления, заданного как вектор 2 на 1 в форме [AzimuthAngle; ElevationAngle] в градусах. Типичным начальным предположением является текущий угол поворота. Азимутальные углы должны быть между -180 и 180. Углы возвышения должны быть между -90 и 90. Углы измеряются в локальной системе координат массива. Для получения подробной информации о локальной системе координат URA введите phased.URA.coordinateSystemInfo. Этот аргумент можно указать как одинарную или двойную точность.

Выходные аргументы

ESTANG

Оценка входящего направления, возвращаемого в виде вектора 2 на 1 [AzimuthAngle; ElevationAngle] в градусах. Азимутальные углы находятся между -180 и 180. Углы возвышения находятся в диапазоне от -90 до 90. Углы измеряются в локальной системе координат массива.

Примеры

развернуть все

Найдите целевое направление Используя различие суммы 2D шпионом монопульса

Открыть сценарий в реальном времени

С помощью URA определите направление цели приблизительно на азимуте 60 ° и отметке 20 °.

array = phased.URA('Size',4);
steeringvec = phased.SteeringVector('SensorArray',array);
tracker = phased.SumDifferenceMonopulseTracker2D('SensorArray',array);
x = steeringvec(tracker.OperatingFrequency,[60.1; 19.5]).';
est_dir = tracker(x,[60; 20])

est_dir = 2×1

   60.1000
   19.5000

Алгоритмы

Моноимпульсный алгоритм суммы и разности используется для оценки направления прихода узкополосного сигнала, падающего на однородную линейную матрицу (ULA). Во-первых, вычислить обычный отклик матрицы, управляемой в направлении поступления ф0. Для ULA направление поступления определяется углом ширины. Чтобы указать, что максимальная ось отклика (MRA) указывает в направлении ф0, задайте веса, которые должны быть

$_{ws} = (1^{,_{}}^{eikdsinstart0,_{}} {eik2dsinstart0}^{, . . ., eik (N_{}} -$ 1) dsinstart0)

где d - расстояние между элементами, а k = 2λ/λ - волновое число. Входящая плоская волна, исходящая из любого произвольного направления, представляется как

$v = (1^{,}^{eikdsinstart,} {eik2dsin}^{, . . ., eik (N}$ − 1) dsinstart)

Обычный отклик этой матрицы на любую входящую плоскую волну задается $_{}^{} как wsHv (« wsHv$ ») и показан на полярном графике ниже как суммарный шаблон. Решетка выполнена с возможностью управления в направлении _ф0 = 30 °.

Второй шаблон, называемый разностным шаблоном, получается с использованием фазированных обратных весов. Веса определяются путем фазового реверсирования последней половины обычного вектора рулевого управления. Для массива с четным числом элементов весами, обращенными по фазе, являются

$_{wd} =−i (1,^{_{}} eikdsinϕ0,^{_{}} eik2dsinϕ0^{...,_{}} {eikN/2dsinϕ0}^{, -eik_{}} {(N/2+1) dsinϕ0}^{..., −eik_{}}$ (N−1) dsinϕ0)

(Для массива с нечетным числом элементов средний вес устанавливается равным нулю). Для удобства используется мультипликативный коэффициент -i. Ответ массива разностей на входящий вектор:

$_{}^{} wdHv (start$ )

На этом рисунке показаны суммарные и разностные диаграммы направленности четырехэлементной однородной линейной матрицы (ULA), направленной на 30 ° от ширины. Элементы матрицы разнесены на половину длины волны. Суммарный шаблон показывает, что массив имеет максимальный отклик при 30 °, а разностный шаблон имеет нулевое значение при 30 °.

Кривая моноимпульсной характеристики получается делением разностной картины на суммарную картину и взятием действительной части.

$R (start) = \frac{_{Re}^{} (}{{wdHv}_{}^{(} start)}$ wsHv (start))

Чтобы использовать моноимпульсную кривую отклика, чтобы получить угол прихода, λ, узкополосного сигнала, x, вычислите

$z = \frac{{Re}_{}^{(}}{_{}^{}}$ wdHxwsHx)

и инвертировать кривую откликов, λ = ^R-1 (z), чтобы получить

Кривая отклика обычно не является единичной и может быть инвертирована только в том случае, если углы прихода лежат в пределах основного лепестка, где она является единичной. На этом рисунке показана кривая монопульного отклика в пределах основного лепестка четырехэлементного массива ULA.

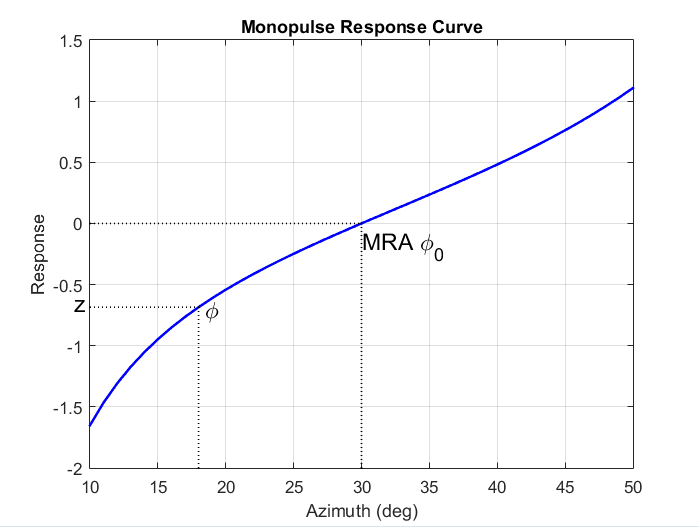
Существует два желательных свойства кривой моноимпульсной реакции. Первое - у него крутой уклон. Крутой склон гарантирует устойчивость к шуму. Второе свойство состоит в том, что основной блок должен быть максимально широким. Крутой наклон обеспечивается большим массивом, но приводит к меньшему материалу. Вам нужно будет обменять одну собственность на другую.

Для получения дополнительной информации см. [1].

Ссылки

[1] Селиктар, Y. Пространственно-временная адаптивная моноимпульсная обработка. Доктор философии. Дипломная работа. Технологический институт Джорджии, Атланта, 1998 год.

[2] Родос, Д. Введение в монопульс. Дедем, Массачусетс: Artech House, 1980.

См. также

azel2phitheta | azel2uv | phitheta2azel | uv2azel

Документация

шаг