Нелинейный индуктор

Индуктор с неидеальным сердечником

Библиотека:
Simscape/Электрическая/Пассивная

Описание

Блок нелинейных индукторов представляет собой индуктор с неидеальным сердечником. Сердечник может быть неидеальным из-за его магнитных свойств и размеров. Блок предоставляет следующие опции параметризации:

Одиночная индуктивность (линейная)

Зависимости между напряжением, током и потоком определяются следующими уравнениями:

$i =_{} iL_{+}$ vGp

$v =_{} \frac{}{}$ NwdФдт

$Λ \frac{=}{_{}}_{}$ LNwiL

где:

v - напряжение на клемме.
i - ток терминала.
iL - ток через индуктор.
Gp - паразитная параллельная проводимость.
Nw - количество витков обмотки.
Λ - магнитный поток.
L - ненасыщенная индуктивность.

Одиночная точка насыщения

Зависимости между напряжением, током и потоком определяются следующими уравнениями:

$i =_{} iL_{+}$ vGp

$v =_{} \frac{}{}$ NwdФдт

$Start= \frac{}{_{}}_{} LNwiL ( для$ ненасыщенных)

$Start= \frac{_{}}{_{}}_{} {LsatNwiL}_{\pm} Фсмещение (для$ насыщенного)

где:

v - напряжение на клемме.
i - ток терминала.
iL - ток через индуктор.
Gp - паразитная параллельная проводимость.
Nw - количество витков обмотки.
Λ - магнитный поток.
Фсмещение - смещение насыщения магнитного потока.
L - ненасыщенная индуктивность.
Lsat - насыщенная индуктивность.

Магнитный поток в зависимости от токовой характеристики

Зависимости между напряжением, током и потоком определяются следующими уравнениями:

$i =_{} iL_{+}$ vGp

$v =_{} \frac{}{}$ NwdФдт

$Λ = f_{} ($ iL)

где:

v - напряжение на клемме.
i - ток терминала.
iL - ток через индуктор.
Gp - паразитная параллельная проводимость.
Nw - количество витков обмотки.
Λ - магнитный поток.

Магнитный поток определяется одномерным табличным просмотром, основанным на векторе значений тока и векторе соответствующих значений магнитного потока, которые вы предоставляете. Эти векторы можно построить, используя либо отрицательные и положительные данные, либо только положительные данные. Если используются только положительные данные, вектор должен начинаться с 0, и отрицательные данные будут автоматически вычисляться поворотом около (0,0).

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля

Зависимости между напряжением, током и потоком определяются следующими уравнениями:

$i =_{} iL_{+}$ vGp

$v =_{} \frac{}{}$ NwdФдт

$_{Φ=B⋅Ae}$

$B = f$ (H)

$H \frac{=_{}}{_{}}_{}$ NwleL

где:

v - напряжение на клемме.
i - ток терминала.
iL - ток через индуктор.
Gp - паразитная параллельная проводимость.
Nw - количество витков обмотки.
Λ - магнитный поток.
B - плотность магнитного потока.
H - напряженность магнитного поля.
le - эффективная длина сердцевины.
Ae - эффективная площадь поперечного сечения сердечника.

Плотность магнитного потока определяется методом одномерного табличного просмотра на основе вектора значений напряженности магнитного поля и вектора соответствующих значений плотности магнитного потока, которые вы предоставляете. Эти векторы можно построить, используя либо отрицательные и положительные данные, либо только положительные данные. Если используются только положительные данные, вектор должен начинаться с 0, и отрицательные данные будут автоматически вычисляться поворотом около (0,0).

Зависимость плотности магнитного потока от напряженности магнитного поля с гистерезисом

Зависимости между напряжением, током и потоком определяются следующими уравнениями:

$i =_{} iL_{+}$ vGp

$v =_{} \frac{}{}$ NwdФдт

$_{Φ=B⋅Ae}$

$B =_{} мк0 (H$ + M)

$H \frac{=_{}}{_{}}_{}$ NwleL

где:

v - напряжение на клемме.
i - ток терминала.
iL - ток через индуктор.
Gp - паразитная параллельная проводимость.
Nw - количество витков обмотки.
Λ - магнитный поток.
B - плотность магнитного потока.
мк0 - магнитная постоянная, проницаемость свободного пространства.
H - напряженность магнитного поля.
М - намагниченность сердечника индуктора.
le - эффективная длина сердцевины.
Ae - эффективная площадь поперечного сечения сердечника.

Намагниченность действует для увеличения плотности магнитного потока, и её величина зависит как от величины тока, так и от истории напряженности поля H. Уравнения Джилеса-Атертона [1, 2] используются для определения М в любой данный момент времени. На рисунке ниже показан типичный график результирующей взаимосвязи между В и Н.

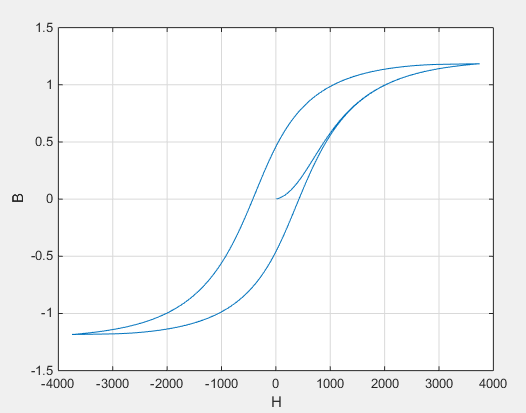
В этом случае намагниченность начинается с нуля, и, следовательно, график начинается с B = H = 0. По мере увеличения напряженности поля график стремится к положительной кривой гистерезиса; затем при развороте скорость изменения Н следует отрицательной кривой гистерезиса. Разница между положительной и отрицательной кривыми обусловлена зависимостью М от истории траектории. Физически поведение соответствует магнитным диполям в сердечнике, выравнивающимся по мере увеличения напряженности поля, но не полностью восстанавливающимся в их исходное положение по мере уменьшения напряженности поля.

Отправной точкой уравнения Джилеса-Атертона является разделение эффекта намагниченности на две части, одна из которых является чисто функцией эффективной напряженности поля (Хефф), а другая - необратимой частью, которая зависит от прошлой истории:

$M =_{} cMan + (1_{-}$ c) Mirr

Термин Человек называется ангистеретической намагниченностью, потому что он не проявляет гистерезиса. Описывается следующей функцией текущего значения эффективной напряженности поля, Heff:

$_{Человек} =_{} Ms (\frac{_{\cot (}}{} \frac{}{{Heffα}_{) -}}$ αHeff)

Эта функция определяет кривую насыщения с предельными значениями ± _Ms и точкой насыщения, определяемыми значением α, ангистеретического коэффициента формы. Его можно приблизительно рассматривать как описание среднего значения двух гистеретических кривых. В блоке «Нелинейный индуктор» задаются значения $_{}_{}$ dMan/dHeffwhen _Heff = 0 и точка [_H1, _B1] на ангистеретической кривой B-H, которые используются для определения значений α и _Ms.

Параметр c является коэффициентом для обратимой намагниченности и определяет, какая часть поведения определена Человеком, а сколько - необратимым термином Мирр. Модель Джилеса-Атертона определяет необратимый термин по частной производной в отношении напряженности поля:

$\begin{array}{l} \frac{_{}}{dMirrdH} \frac{=_{} {Man}_{-}}{{MirrKδ}_{-} α_{(}} \\ Man - \begin{array}{l} Mirr) \\ δ & = {1if \end{array} \end{array}$ H≥0−1if H < 0

Сравнение этого уравнения со стандартным дифференциальным уравнением первого порядка показывает, что при приращениях напряженности поля, H, необратимый член Мирр пытается отследить обратимый член Man, но с переменным коэффициентом усиления трекинга $1 / (Kδ -_{α} (_{Man} -$ Mirr)). Ошибка отслеживания действует для создания гистерезиса в точках, где δ меняет знак. Основным параметром, формирующим необратимую характеристику, является K, который называется коэффициентом объемной связи. Параметр α называется междоменным коэффициентом связи, а также используется для определения эффективной напряженности поля, используемой при определении ангистеретической кривой:

$_{Heff} = H$ + αM

Значение α влияет на форму кривой гистерезиса, большие значения, действующие для увеличения перехватов по оси В. Однако обратите внимание, что для стабильности термин $Kδ - α_{(}_{Man -}$ Mirr) должен быть положительным для δ > 0 и отрицательным для δ < 0. Поэтому допустимы не все значения α, причем типичным максимальным значением является значение порядка 1e-3.

Процедура поиска приблизительных значений коэффициентов уравнения Джилеса-Атертона

Можно определить репрезентативные параметры для коэффициентов уравнений с помощью следующей процедуры.

Предоставьте значение для ангистеретического градиента B-H, когда H равен нулю ( $_{}_{}$ dMan/dHeffwhen Heff = 0) плюс точка данных [H1, B1] на ангистеретической кривой B-H. Из этих значений инициализация блока определяет значения α и Ms.
Установите коэффициент для обратимой намагниченности, параметр c для достижения правильного начального градиента B-H при запуске моделирования с [H B] = [0 0]. Значение c приблизительно равно отношению этого начального градиента к ангистеретическому градиенту B-H, когда Н равен нулю. Значение c должно быть больше 0 и меньше 1.
Установите коэффициент связи Bulk, параметр K в приблизительную величину H, когда B = 0 на положительной кривой гистерезиса.
Начните с α очень маленького и постепенно увеличивайте значение B при пересечении линии H = 0. Типичное значение находится в диапазоне от 1e-4 до 1e-3. Слишком большие значения приведут к тому, что градиент кривой B-H будет стремиться к бесконечности, которая является нефизической и порождает ошибку утверждения во время выполнения.

Иногда необходимо выполнить итерацию на этих четырех шагах, чтобы получить хорошее совпадение с предопределенной кривой B-H.

Порты

Сохранение

развернуть все

`+` - Положительный терминал
электрический

Электрический консервационный порт, связанный с положительным напряжением индуктора.

`-` - Отрицательный вывод
электрический

Электрический консервационный порт, связанный с отрицательным напряжением индуктора.

Параметры

развернуть все

Главный

`Parameterized by` - Параметризация блока
`Single saturation point` (по умолчанию) | `Single inductance (linear)` | `Magnetic flux versus current characteristic` | `Magnetic flux density versus magnetic field strength characteristic` | `Magnetic flux density versus magnetic field strength characteristic with hysteresis`

Выберите один из следующих методов параметризации блока:

Single inductance (linear) - Обеспечить значения количества витков, ненасыщенной индуктивности и паразитной параллельной проводимости.
Single saturation point - Обеспечить значения числа витков, ненасыщенных и насыщенных индуктивностей, магнитного потока насыщения и паразитной параллельной проводимости. Это параметр по умолчанию.
Magnetic flux versus current characteristic - В дополнение к числу витков и величине паразитной параллельной проводимости, обеспечить вектор тока и вектор магнитного потока, чтобы заполнить таблицу зависимости магнитного потока от тока.
Magnetic flux density versus magnetic field strength characteristic - В дополнение к числу витков и величине паразитной параллельной проводимости, предоставить значения для эффективной длины сердечника и площади поперечного сечения, а также вектора напряженности магнитного поля и вектора плотности магнитного потока для заполнения таблицы зависимости плотности магнитного потока от плотности магнитного поля.
Magnetic flux density versus magnetic field strength characteristic with hysteresis - в дополнение к числу витков и эффективной длине сердечника и площади поперечного сечения, предоставить значения для начального градиента кривой В-Н, плотность магнитного потока и напряженность поля в определенной точке на кривой B-H, а также коэффициент обратимой намагниченности, коэффициент объемной связи, и коэффициент межполюсной связи для определения плотности магнитного потока как функции величины тока и истории напряженности поля.

`Number of turns` - Общее количество оборотов
`10` (по умолчанию)

Общее число витков провода, намотанного вокруг сердечника индуктора.

`Unsaturated inductance` - Ненасыщенная индуктивность
`2e-4` `H` (по умолчанию)

Величина индуктивности, используемая при работе индуктора в его линейной области.

Зависимости

Этот параметр отображается только при выборе Single inductance (linear) или Single saturation point для параметра Parameterized by.

`Saturated inductance` - Насыщенная индуктивность
`1e-4` `H` (по умолчанию)

Величина индуктивности, используемая при работе индуктора за пределами его точки насыщения.

Зависимости

Этот параметр отображается только при выборе Single saturation point для параметра Parameterized by.

`Saturation magnetic flux` - Магнитный поток насыщения
`1.3e-05` `Wb` (по умолчанию)

Величина магнитного потока, при которой индуктор насыщается.

Зависимости

Этот параметр отображается только при выборе Single saturation point для параметра Parameterized by.

`Current vector, i` - Вектор текущих данных
`[0, .64, 1.28, 1.92, 2.56, 3.2]` `A` (по умолчанию)

Текущие данные, используемые для заполнения таблицы поиска по току магнитного потока.

Зависимости

Этот параметр отображается только при выборе Magnetic flux versus current characteristic для параметра Parameterized by.

`Magnetic flux vector, phi` - Данные о магнитном потоке
`[0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5` `Wb` (по умолчанию)

Данные магнитного потока, используемые для заполнения таблицы сравнения магнитного потока и тока.

Зависимости

Этот параметр отображается только при выборе Magnetic flux versus current characteristic для параметра Parameterized by.

`Magnetic field strength vector, H` - Вектор напряженности магнитного поля
`[0, 200, 400, 600, 800, 1000]` `A/m` (по умолчанию)

Данные напряженности магнитного поля, используемые для заполнения таблицы сравнения плотности магнитного потока и напряженности магнитного поля.

Зависимости

Этот параметр отображается только при выборе Magnetic flux density versus magnetic field strength characteristic для параметра Parameterized by.

`Magnetic flux density vector, B` - Данные о плотности магнитного потока
`[0, .81, 1.25, 1.42, 1.48, 1.49]` `T` (по умолчанию)

Данные плотности магнитного потока, используемые для заполнения таблицы сравнения плотности магнитного потока и напряженности магнитного поля.

Зависимости

`Effective length` - Эффективная длина сердечника
`0.032` `m` (по умолчанию)

Эффективная длина сердечника, то есть среднее расстояние магнитного пути.

Зависимости

Этот параметр отображается только при выборе Magnetic flux density versus magnetic field strength characteristic или Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Effective cross-sectional area` - Эффективная площадь поперечного сечения
`1.6e-5` `m^2` (по умолчанию)

Эффективная площадь поперечного сечения сердечника, то есть средняя площадь магнитного пути.

Зависимости

`Anhysteretic B-H gradient when H is zero` - Ангистеретический градиент B-H вокруг нулевой напряженности поля
`0.005` `m*T/A` (по умолчанию)

Градиент ангистеретической (без гистерезиса) кривой B-H вокруг нулевой напряженности поля. Установите его в среднее значение градиента кривых положительного и отрицательного гистерезиса.

Зависимости

Этот параметр отображается только при выборе Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Flux density point on anhysteretic B-H curve` - Точка плотности потока на ангистеретической кривой B-H
`1.49` `T` (по умолчанию)

Укажите точку на анистеретической кривой, указав значение плотности потока. Наиболее точным вариантом является выбор точки при высокой напряженности поля, где кривые положительного и отрицательного гистерезиса выравниваются.

Зависимости

`Corresponding field strength` - Соответствующая напряженность поля
`1000` `A/m` (по умолчанию)

Соответствующая напряженность поля для точки, определяемой точкой плотности потока на параметре ангистеретической кривой B-H.

Зависимости

`Coefficient for reversible magnetization, c` - Коэффициент реверсивной намагниченности
`0.1` (по умолчанию)

Доля обратимой намагниченности. Значение должно быть больше нуля и меньше единицы.

Зависимости

`Bulk coupling coefficient, K` - Коэффициент сцепления насыпью
`200` `A/m` (по умолчанию)

Параметр Джилса-Атертона, который в основном управляет величиной напряженности поля, при которой кривая B-H пересекает линию нулевой плотности потока.

Зависимости

`Inter-domain coupling factor, alpha` - Междоменный коэффициент связи
`1e-4` (по умолчанию)

Параметр Джилса (Jiles) - Атертона (Atherton), который в первую очередь влияет на точки, в которых кривые B-H пересекают линию нулевой напряженности поля. Типичные значения находятся в диапазоне от 1e-4 до 1e-3.

Зависимости

`Averaging period for power logging` - Период усреднения для регистрации мощности
`0` `s` (по умолчанию)

Период усреднения для расчета гистерезисных потерь. Эти потери пропорциональны площади, ограниченной траекторией B-H. Если блок возбуждается на известной фиксированной частоте, можно установить это значение в соответствующий период возбуждения для вычисления гистерезисных потерь. В этом случае блок регистрирует потери гистерезиса один раз за цикл переменного тока в переменной power_dissipated. Если используется решатель с фиксированным шагом, это значение должно быть целым числом, кратным размеру шага моделирования.

Если блок не возбуждается на известной фиксированной частоте, установите для этого параметра значение 0. В этом случае блоки устанавливаются power_dissipated до нуля, и можно вычислить фактическую потерю гистерезиса путем последующей обработки регистрируемой переменной power_instantaneous.

Зависимости

Этот параметр отображается только при выборе Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Параметризовано по (Parameterized by) на вкладке Главная (Main).

`Parasitic parallel conductance` - Паразитная параллельная проводимость
`1e-9` `1/Ohm` (по умолчанию)

Этот параметр используется для представления небольших паразитных эффектов. Для моделирования некоторых топологий цепи может потребоваться небольшая параллельная проводимость.

`Interpolation option` - Опция интерполяции
`Linear` (по умолчанию) | `Smooth`

Опция интерполяции таблицы подстановки. Выберите один из следующих методов интерполяции:

Linear - Выберите этот параметр, чтобы получить наилучшую производительность.
Smooth - выберите эту опцию, чтобы создать непрерывную кривую с непрерывными производными первого порядка.

Дополнительные сведения о алгоритмах интерполяции см. на странице ссылок на блоки таблицы поиска PS (1D).

Зависимости

Этот параметр отображается только при выборе Magnetic flux versus current characteristic или Magnetic flux density versus magnetic field strength characteristic для параметра Параметризовано по (Parameterized by) на вкладке Главная (Main).

Начальные условия

`Specify initial state by` - Вариант спецификации исходного состояния
`Current` (по умолчанию) | `Magnetic flux`

Выберите соответствующую опцию спецификации начального состояния:

Current - Укажите исходное состояние индуктора по исходному току через индуктор (iL). Это параметр по умолчанию.
Magnetic flux - Указать исходное состояние индуктора по магнитному потоку.

Зависимости

Этот параметр не отображается при выборе Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Initial current` - Начальный ток
`0` `A` (по умолчанию)

Начальное значение тока, используемое для вычисления значения магнитного потока в нуль времени. Это ток, проходящий через индуктор. Компонентный ток состоит из тока, проходящего через индуктор, и тока, проходящего через паразитную параллельную проводимость.

Зависимости

Этот параметр отображается только при выборе Current для параметра Specify initial state by.

`Initial magnetic flux` - Начальный магнитный поток
`0` `Wb` (по умолчанию)

Значение магнитного потока в нуль времени.

Зависимости

Этот параметр отображается только при выборе Magnetic flux для параметра Specify initial state by.

`Initial magnetic flux density` - Начальная плотность магнитного потока
`0` `T` (по умолчанию)

Значение плотности магнитного потока в нуль времени.

Зависимости

`Initial field strength` - Начальная напряженность поля
`0` `A/m` (по умолчанию)

Значение напряженности магнитного поля в нуль времени.

Зависимости

Примеры модели

Нелинейные характеристики индуктора

Сравнение поведения нелинейных индукторов для различных параметризаций. Начиная со значений фундаментальных параметров, получаются параметры для линейных и нелинейных представлений. Эти параметры затем используются в Simscape™ модели, и результаты моделирования сравниваются.

Индуктор с гистерезисом

Как изменение коэффициентов уравнений уравнений гистерезиса Джилеса-Атертона влияет на результирующую кривую B-H. Параметры моделирования сконфигурированы для выполнения четырех полных циклов переменного тока с начальной напряженностью поля (H) и плотностью магнитного потока (B), которые установлены на ноль.

Ссылки

[1] Jiles, D. C. и D. L. Атертон. «Теория ферромагнитного гистерезиса». Журнал магнетизма и магнитных материалов. Том 61, 1986, стр. 48-60.

[2] Jiles, D. C. и D. L. Атертон. «Ферромагнитный гистерезис». Транзакции IEEE ^® по магнитам. т. 19, № 5, 1983, стр. 2183-2184.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Представлен в R2012b

Документация

Нелинейный индуктор

Описание

Одиночная индуктивность (линейная)

Одиночная точка насыщения

Магнитный поток в зависимости от токовой характеристики

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля

Зависимость плотности магнитного потока от напряженности магнитного поля с гистерезисом

Процедура поиска приблизительных значений коэффициентов уравнения Джилеса-Атертона

Порты

Сохранение

+ - Положительный терминал электрический

- - Отрицательный вывод электрический

Параметры

Главный

Number of turns - Общее количество оборотов 10 (по умолчанию)

Unsaturated inductance - Ненасыщенная индуктивность 2e-4 H (по умолчанию)

Зависимости

Saturated inductance - Насыщенная индуктивность 1e-4 H (по умолчанию)

Зависимости

Saturation magnetic flux - Магнитный поток насыщения 1.3e-05 Wb (по умолчанию)

Зависимости

Current vector, i - Вектор текущих данных [0, .64, 1.28, 1.92, 2.56, 3.2] A (по умолчанию)

Зависимости

Magnetic flux vector, phi - Данные о магнитном потоке [0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5 Wb (по умолчанию)

Зависимости

Magnetic field strength vector, H - Вектор напряженности магнитного поля [0, 200, 400, 600, 800, 1000] A/m (по умолчанию)

Зависимости

Magnetic flux density vector, B - Данные о плотности магнитного потока [0, .81, 1.25, 1.42, 1.48, 1.49] T (по умолчанию)

Зависимости

Effective length - Эффективная длина сердечника 0.032 m (по умолчанию)

Зависимости

Effective cross-sectional area - Эффективная площадь поперечного сечения 1.6e-5 m^2 (по умолчанию)

Зависимости

Anhysteretic B-H gradient when H is zero - Ангистеретический градиент B-H вокруг нулевой напряженности поля 0.005 m*T/A (по умолчанию)

Зависимости

Flux density point on anhysteretic B-H curve - Точка плотности потока на ангистеретической кривой B-H 1.49 T (по умолчанию)

Зависимости

Corresponding field strength - Соответствующая напряженность поля 1000 A/m (по умолчанию)

Зависимости

Coefficient for reversible magnetization, c - Коэффициент реверсивной намагниченности 0.1 (по умолчанию)

Зависимости

Bulk coupling coefficient, K - Коэффициент сцепления насыпью 200 A/m (по умолчанию)

Зависимости

Inter-domain coupling factor, alpha - Междоменный коэффициент связи 1e-4 (по умолчанию)

Зависимости

Averaging period for power logging - Период усреднения для регистрации мощности 0 s (по умолчанию)

Зависимости

Parasitic parallel conductance - Паразитная параллельная проводимость 1e-9 1/Ohm (по умолчанию)

Interpolation option - Опция интерполяции Linear (по умолчанию) | Smooth

Зависимости

Начальные условия

Specify initial state by - Вариант спецификации исходного состояния Current (по умолчанию) | Magnetic flux

Зависимости

Initial current - Начальный ток 0 A (по умолчанию)

Зависимости

Initial magnetic flux - Начальный магнитный поток 0 Wb (по умолчанию)

Зависимости

Initial magnetic flux density - Начальная плотность магнитного потока 0 T (по умолчанию)

Зависимости

Initial field strength - Начальная напряженность поля 0 A/m (по умолчанию)

Зависимости

Примеры модели

Нелинейные характеристики индуктора

Индуктор с гистерезисом

Ссылки

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Документация Simscape Electrical

Поддержка

`+` - Положительный терминал
электрический

`-` - Отрицательный вывод
электрический

`Number of turns` - Общее количество оборотов
`10` (по умолчанию)

`Unsaturated inductance` - Ненасыщенная индуктивность
`2e-4` `H` (по умолчанию)

`Saturated inductance` - Насыщенная индуктивность
`1e-4` `H` (по умолчанию)

`Saturation magnetic flux` - Магнитный поток насыщения
`1.3e-05` `Wb` (по умолчанию)

`Current vector, i` - Вектор текущих данных
`[0, .64, 1.28, 1.92, 2.56, 3.2]` `A` (по умолчанию)

`Magnetic flux vector, phi` - Данные о магнитном потоке
`[0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5` `Wb` (по умолчанию)

`Magnetic field strength vector, H` - Вектор напряженности магнитного поля
`[0, 200, 400, 600, 800, 1000]` `A/m` (по умолчанию)

`Magnetic flux density vector, B` - Данные о плотности магнитного потока
`[0, .81, 1.25, 1.42, 1.48, 1.49]` `T` (по умолчанию)

`Effective length` - Эффективная длина сердечника
`0.032` `m` (по умолчанию)

`Effective cross-sectional area` - Эффективная площадь поперечного сечения
`1.6e-5` `m^2` (по умолчанию)

`Anhysteretic B-H gradient when H is zero` - Ангистеретический градиент B-H вокруг нулевой напряженности поля
`0.005` `m*T/A` (по умолчанию)

`Flux density point on anhysteretic B-H curve` - Точка плотности потока на ангистеретической кривой B-H
`1.49` `T` (по умолчанию)

`Corresponding field strength` - Соответствующая напряженность поля
`1000` `A/m` (по умолчанию)

`Coefficient for reversible magnetization, c` - Коэффициент реверсивной намагниченности
`0.1` (по умолчанию)

`Bulk coupling coefficient, K` - Коэффициент сцепления насыпью
`200` `A/m` (по умолчанию)

`Inter-domain coupling factor, alpha` - Междоменный коэффициент связи
`1e-4` (по умолчанию)

`Averaging period for power logging` - Период усреднения для регистрации мощности
`0` `s` (по умолчанию)

`Parasitic parallel conductance` - Паразитная параллельная проводимость
`1e-9` `1/Ohm` (по умолчанию)

`Interpolation option` - Опция интерполяции
`Linear` (по умолчанию) | `Smooth`

`Specify initial state by` - Вариант спецификации исходного состояния
`Current` (по умолчанию) | `Magnetic flux`

`Initial current` - Начальный ток
`0` `A` (по умолчанию)

`Initial magnetic flux` - Начальный магнитный поток
`0` `Wb` (по умолчанию)

`Initial magnetic flux density` - Начальная плотность магнитного потока
`0` `T` (по умолчанию)

`Initial field strength` - Начальная напряженность поля
`0` `A/m` (по умолчанию)

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™