Однополярный шаговый двигатель

Шаговый двигатель с центральными отводами на двухфазных обмотках

Библиотека:
Simscape/Электрические/Электромеханические/Нежелательные и шаговые

Описание

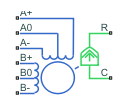
Блок однополярного шагового двигателя представляет шаговый двигатель, который имеет центральные отводы на двухфазных обмотках. Токи обмоток и механический выход определяются следующими уравнениями:

$_{eA} + =_{} -_{} Km$

$_{eA} -_{=}_{Km}$

$_{eB} +_{=}_{Km}$

$_{eB} - =_{} -_{} Km$

$\frac{_{diA}}{+} dt_{=} ({vA}_{+} -_{} RiA$ + − eA + )/L

$\frac{_{dIa}}{-} dt_{=} ({vA}_{-} -_{} RiA$ − − eA − )/L

$\frac{_{diB}}{+} dt_{=} ({vB}_{+} -_{} RiB$ + − eB + )/L

$\frac{_{diB}}{-} dt_{=} ({vB}_{-} -_{} RiB$ − − eB − )/L

$\frac{}{Jdü dt} + {Bλ}_{}$ = Te

$_{Те}_{=−Km}_{}_{} \frac{_{}_{}}{_{}} (iA +−iA−−eA +−eA−Rm) {грех}_{}_{}_{(Nrθ) +Km}_{} \frac{_{}_{}}{_{}} {(iB +−iB−−eB +−eB−Rm)}_{}, потому что_{}_{}$ (Nrθ) −Tdsin (4Nrθ)

$\frac{}{dü dt} =$ λ

где:

_eA + - это обратная ЭДС, индуцированная через A + - A0 полувымотку.
_eA- это задняя ЭДС, индуцированная через A- до A0 полуобмотку.
_eB + - обратная ЭДС, индуцированная через B + до B0 полувымотки.
_eB- - задняя ЭДС, индуцированная через В- до B0 полуобмотки.
_iA + - ток, протекающий от порта A + к порту отвода центра A0.
_iA- ток, протекающий от порта A- к порту отвода центра A0.
_iB + - ток, протекающий от порта B + к порту отвода центра B0.
_{iB -} ток, протекающий от порта B- к порту отвода центра B0.
_vA + - напряжение в порту A + относительно порта центрального ответвления A0.
_vA- напряжение в порту A- относительно порта центрального ответвления A0.
_vB + - напряжение в порту B + относительно порта центрального ответвления B0.
_vB- напряжение в порту B- относительно порта центрального ответвления B0.
_Km - постоянный крутящий момент двигателя.
_Nr - количество зубьев на каждом из двух полюсов ротора. Параметр Full step size (Полный размер шага) равен (λ/2 )/_Nr.
R - сопротивление полуобмотки. Например, это сопротивление между портами A + и A0.
L - индуктивность полуобмотки. Например, это индуктивность между портами A + и A0.
Rm - сопротивление намагничиванию.
B - гашение вращения.
J - инерция.
λ - частота вращения ротора.
Δ - угол ротора.
_Td - амплитуда крутящего момента фиксатора.
_Te - электрический крутящий момент.

Если начальный ротор равен нулю или является кратным (λ/2 )/_Nr, то ротор выравнивается с обмоткой фазы А. Если положительный ток течет от порта A + к порту отвода центра A0, то степпер действует так, чтобы оставаться выровненным с фазой A. Эквивалентно, положительный ток, протекающий от центрального порта отвода A0 к A-порту, также действует на ротор, чтобы оставаться выровненным с A-фазой.

Блок однополярного шагового двигателя создает положительный крутящий момент, действующий от механических портов C к R для любой из следующих последовательностей. Обе последовательности предполагают, что начальный угол ротора равен нулю или несколько кратен (λ/2 )/_Nr.

Последовательность	Центральные отводы, подключенные к земле	Центральные отводы, подключенные к положительному источнику питания
1	Положительный ток от A + до A0	Положительный ток от A0 до A-
2	Положительный ток от В + до B0	Положительный ток от B0 до B-
3	Положительный ток от А до A0	Положительный ток от A0 до A-
4	Положительный ток от В- до B0	Положительный ток от B0 до B-

Усредненный режим

Если для параметра Режим моделирования (Simulation mode) задано значение Averaged, как для блока однополярного шагового двигателя, так и для блока драйвера однополярного шагового двигателя, который управляет им, отдельные шаги не моделируются. Это может быть хорошим способом ускорить моделирование. В усредненном режиме в условиях отсутствия проскальзывания двигатель и привод представлены линейной системой второго порядка, которая отслеживает заданную скорость шага. Требуемая ступенчатая скорость определяется непосредственно по напряжению на A + и A-. Так, например, напряжение + 10 В на A + и A- клеммах интерпретируется как требование скорости шага в десять шагов в секунду. Дополнительные сведения о подключении драйвера однополярного шагового двигателя к контроллеру угла шага см. на справочной странице «Драйвер однополярного шагового двигателя».

Усредненный режим включает в себя блок оценки проскальзывания для прогнозирования того, проскальзывал ли бы шаговый двигатель при работе в режиме моделирования степпинга. Проскальзывание прогнозируют, если крутящий момент двигателя превышает вектор значения параметра максимальных значений крутящего момента в течение более чем одного периода шага, причем период шага определяют из текущей требуемой скорости шага. После обнаружения проскальзывания моделирование будет продолжено или остановлено с ошибкой в соответствии со значением параметра Action on slipping. При выборе действия, позволяющего продолжить моделирование, обратите внимание, что результаты моделирования могут быть неверными: при проскальзывании крутящий момент, создаваемый двигателем, как правило, не будет максимальным доступным крутящим моментом; максимальный крутящий момент достигается только в том случае, если шаговый контроллер обнаруживает проскальзывание и соответственно регулирует команду скорости шага.

Динамика эквивалентной системы второго порядка определяется из значений, заданных для параметров команды Приблизительная суммарная инерция нагрузки (Approximate total load inertia) и Максимальная скорость шага (Maximum step rate). Важно установить как можно более точные значения для этих параметров, чтобы команда скорости шага отслеживалась, а блок не генерировал ложных предупреждений о проскальзывании или ошибок.

Если двигатель работает в усредненном режиме с открытыми дополнительными тепловыми портами (см. раздел Тепловые порты), то тепло добавляется к тепловым портам при условии, что обмотки всегда питаются, даже если команда скорости шага равна нулю. Блок выполняет регулировку на половину ступенчатого перемещения и на пониженный крутящий момент (и токи обмотки) при более высоких скоростях. Чтобы эти регулировки были правильными, вектор максимальных значений параметров крутящего момента должен быть верным. Для половинной ступенчатой обработки при нулевой скорости теплота, генерируемая блоком, представляет собой среднее значение теплоты, генерируемой при остановке на половинной ступени и на полной ступени.

При моделировании или прогнозировании проскальзывания MathWorks рекомендует выполнить несколько прогонов проверки, сравнивая степпинг и усредненный режимы, прежде чем использовать усредненное представление модели для расчетных исследований.

Тепловые порты

Блок имеет пять опциональных тепловых портов, по одному для каждой из четырех полуобмоток и по одному для ротора. По умолчанию эти порты скрыты. Чтобы открыть тепловые порты, щелкните правой кнопкой мыши блок в модели, а затем в контекстном меню выберите «Simscape» > «Block choices» > «Show thermal port». Это действие отображает тепловые порты на значке блока и отображает параметры Температурная зависимость (Temperature Dependence) и Тепловой порт (Thermal Port). Эти параметры описаны далее на этой справочной странице.

Используйте тепловые порты для моделирования влияния сопротивления меди и потерь железа, которые преобразуют электроэнергию в тепло. Дополнительные сведения об использовании тепловых портов в блоках привода см. в разделе Моделирование тепловых эффектов во вращательных и поступательных приводах.

Допущения и ограничения

Модель игнорирует эффекты магнитного насыщения и любую магнитную связь между фазами.
Когда Вы выберете моделирование Начала из флажка устойчивого состояния в блоке Конфигурации Решающего устройства Simscape™, этот блок не инициализирует Начальную угловую стоимость ротора между-π и π.
Предполагается, что все четыре полуобмотки идентичны и поэтому имеют одинаковый температурный коэффициент сопротивления, альфа и одинаковую тепловую массу.
Для использования усредненного режима блок однополярного шагового двигателя должен быть непосредственно соединен с блоком драйвера однополярного шагового двигателя, также работающим в усредненном режиме.
Усредненный режим является аппроксимацией, и точного отслеживания шага по сравнению со степпингом не следует ожидать.
Обнаружение проскальзывания в усредненном режиме является приблизительным и зависит от хорошей оценки инерции нагрузки и максимальной скорости шага. Неправильные значения могут привести к обнаружению ложного проскальзывания.
При моделировании проскальзывания в усредненном режиме предполагается, что контроллер шагового двигателя регулирует команду скорости шага так, чтобы достичь максимально возможного крутящего момента.

Порты

Сохранение

развернуть все

`A+` - Верхнее А-фазное электрическое соединение
электрический

Порт экономии электроэнергии, связанный с верхним А-фазным электрическим соединением.

`A0` - Соединение A-фазного центрального ответвления
электрический

Электрический консервационный порт, связанный с A-фазным отводом.

`A-` - Нижнее А-фазное электрическое соединение
электрический

Порт экономии электроэнергии, связанный с нижним А-фазным электрическим соединением.

`B+` - Верхнее B-фазное электрическое соединение
электрический

Порт экономии электроэнергии, связанный с верхним B-фазным электрическим соединением.

`B0` - Соединение B-фазного центрального ответвления
электрический

Электрический консервационный порт, связанный с подключением к центру B-фазы.

`B-` - Нижнее B-фазное электрическое соединение
электрический

Порт экономии электроэнергии, связанный с нижним B-фазным электрическим соединением.

`C` - Дело
механический

Механическое поворотное защитное отверстие, связанное с корпусом.

`R` - Ротор
механический

Механическое отверстие для сохранения вращения, связанное с ротором.

`HA+` - Тепловой порт для обмотки между A + и A0
тепловой

Тепловой порт для обмотки между A + и A0. Дополнительные сведения см. в разделе Тепловые порты.

`HA-` - Тепловой порт для обмотки между A- и A0
тепловой

Тепловой порт для обмотки между A- и A0. Дополнительные сведения см. в разделе Тепловые порты.

`HB+` - Тепловой порт для обмотки между B + и B0
тепловой

Тепловой порт для обмотки между B + и B0. Дополнительные сведения см. в разделе Тепловые порты.

`HB-` - Тепловой порт для обмотки между B- и B0
тепловой

Тепловой порт для обмотки между B и B. Дополнительные сведения см. в разделе Тепловые порты.

`HR` - Тепловой порт ротора
тепловой

Тепловое отверстие для ротора. Дополнительные сведения см. в разделе Тепловые порты.

Параметры

развернуть все

Электрический крутящий момент

`Simulation mode` - Режим моделирования
`Stepping` (по умолчанию) | `Averaged`

Выбрать Stepping или Averaged. Использовать Averaged только если блок подключен непосредственно к блоку драйвера однополярного шагового двигателя, также работающему в усредненном режиме.

`Vector of rotational speeds` - Вектор скоростей вращения
`[0, 1000, 3000]` `rpm` (по умолчанию)

Вектор скоростей вращения, при которых определяют максимальные значения крутящего момента, для прогнозирования проскальзывания.

Зависимости

Этот параметр отображается только в том случае, если для параметра Режим моделирования (Simulation mode) задано значение Averaged.

`Vector of maximum torque values` - Вектор максимальных значений крутящего момента
`[2, 2, 1]` `N*m` (по умолчанию)

Вектор максимальных значений крутящего момента, используемый для прогнозирования проскальзывания в сочетании с параметром Vector of rotation speeds. Максимальные значения крутящего момента часто указываются в спецификации и должны соответствовать напряжению питания и типу ступеней (половина шага или полный шаг), указанным в водителе.

Зависимости

`Action on slipping` - Действие при обнаружении проскальзывания
`none` (по умолчанию) | `warn` | `error`

Выберите действие для блока, выполняемое во время моделирования при обнаружении проскальзывания:

none - Продолжить моделирование, ограничив крутящий момент нагрузки в соответствии с вектором максимальных значений крутящего момента.
warn - Продолжить моделирование, ограничив крутящий момент нагрузки в соответствии с вектором максимальных значений крутящего момента, и создать предупреждение о проскальзывании ротора.
error - Остановите моделирование и выдайте сообщение об ошибке при проскальзывании ротора.

Обратите внимание, что при выборе действия, позволяющего продолжить моделирование, результаты моделирования могут быть неверными: при проскальзывании крутящий момент, создаваемый двигателем, как правило, не будет максимальным доступным крутящим моментом; максимальный крутящий момент достигается только в том случае, если шаговый контроллер обнаруживает проскальзывание и соответственно регулирует команду скорости шага.

Зависимости

`Approximate total load inertia` - Приблизительная суммарная инерция нагрузки
`1e-4` `kg*m^2` (по умолчанию)

Приблизительная суммарная инерция нагрузки, включая инерцию ротора. Это значение используется для прогнозирования случаев проскальзывания из-за необходимости быстрого ускорения.

Зависимости

`Maximum step rate command` - Команда максимальной скорости шага
`10` `Hz` (по умолчанию)

Максимальная частота шагов, которую будет использовать система. Он используется для определения подходящей полосы пропускания для приближения системы второго порядка к шаговому двигателю и приводу.

Зависимости

`Half-winding resistance` - Сопротивление полуобмотки
`0.55` `Ohm` (по умолчанию)

Половина сопротивления фазных обмоток А и В, измеренного между A + и A- и B + и B- портами.

Зависимости

Этот параметр отображается только в том случае, если для параметра Режим моделирования (Simulation mode) задано значение Stepping.

`Half-winding inductance` - Индуктивность полуобмотки
`1.5e-3` `H` (по умолчанию)

Половина индуктивности фазных обмоток А и В, измеренная между A + и A- и B + и B- портами.

Зависимости

`Motor torque constant` - Постоянный крутящий момент двигателя
`0.19` `N*m/A` (по умолчанию)

Постоянная крутящего момента двигателя _Km.

Зависимости

`Detent torque` - Момент фиксации
`0` `N*m` (по умолчанию)

Амплитуда изменения синусоидального крутящего момента, наблюдаемая при вращении вала двигателя без питания.

Зависимости

`Magnetizing resistance` - Сопротивление намагничиванию
`inf` `Ohm` (по умолчанию) | положительный скаляр

Общее сопротивление намагничиванию, наблюдаемое от каждой из фазных обмоток, например, через A + и A0. Значение должно быть больше нуля. Значение по умолчанию: Inf, что подразумевает отсутствие потерь железа.

Зависимости

`Full step size` - Полный размер шага
`1.8` `deg` (по умолчанию)

Размер шага при изменении полярности фазного тока A или B. Значение по умолчанию: 1.8°.

`Coefficient of coupling` - Коэффициент сцепления для взаимной индуктивности
`0` (по умолчанию)

Коэффициент сцепления обмоток на взаимную индуктивность.

Механический

`Rotor inertia` - Инерция ротора
`4.5e-5` `kg*m^2` (по умолчанию)

Сопротивление ротора изменению движения двигателя. Значение может быть равно нулю.

`Rotor damping` - Демпфирование ротора
`8.0e-4` `N*m/(rad/s)` (по умолчанию)

Энергия, рассеиваемая ротором. Значение может быть равно нулю.

`Initial rotor speed` - Начальная частота вращения ротора
`0` `rpm` (по умолчанию)

Частота вращения ротора в начале моделирования.

`Initial rotor angle` - Начальный угол ротора
`0` `deg` (по умолчанию)

Угол ротора в начале моделирования.

Температурная зависимость

Эта вкладка отображается только для блоков с открытыми тепловыми портами. Дополнительные сведения см. в разделе Тепловые порты.

`Resistance temperature coefficient` - Температурный коэффициент сопротивления
`3.93e-3` `1/K` (по умолчанию)

Параметр α в уравнении, определяющий сопротивление как функцию температуры, как описано в Тепловой модели для блоков привода. Предполагается, что все обмотки выполнены из одного материала и поэтому имеют одинаковый температурный коэффициент сопротивления.

Зависимости

Этот параметр отображается только в том случае, если для параметра Режим моделирования (Simulation mode) в параметре Электрический крутящий момент (Electrical Torque) задано значение Stepping.

`Measurement temperature` - Температура измерения
`25` `degC` (по умолчанию)

Температура, для которой определены параметры двигателя.

`Vector of maximum torque values at second measurement temperature` - Вектор максимальных значений крутящего момента при второй температуре измерения
`[1.7, 1.7, .85]` `N*m` (по умолчанию)

Вектор максимальных значений крутящего момента при второй температуре измерения.

Зависимости

`Second measurement temperature` - Температура второго измерения
`125` `degC` (по умолчанию)

Вторая температура измерения.

Зависимости

`Stepping mode` - Шаговый режим
`Full stepping` (по умолчанию) | `Half stepping`

Укажите степпинг-режим.

Зависимости

Тепловой порт

`Half-winding thermal mass` - Тепловая масса полуобмотки
`100` `J/K` (по умолчанию)

Тепловая масса для половины обмотки A или B. Тепловая масса - это энергия, необходимая для повышения температуры на один градус. Предполагается, что все четыре полуобмотки имеют одинаковую тепловую массу.

`Half-winding initial temperatures, [T_A+ T_A- T_B+ T_B-]` - Начальные температуры полуобмотки
`[25, 25, 25, 25]` `degC` (по умолчанию)

Вектор строки 1 на 4, определяющий температуру четырех полуобмоток в начале моделирования.

`Rotor thermal mass` - Тепловая масса ротора
`50` `J/K` (по умолчанию)

Тепловая масса ротора, то есть энергия, необходимая для повышения температуры ротора на один градус.

`Rotor initial temperature` - Начальная температура ротора
`25` `degC` (по умолчанию)

Температура ротора в начале моделирования.

`Percentage of magnetizing resistance associated with the rotor` - Процент сопротивления намагничиванию, связанный с ротором
`90` (по умолчанию)

Процент сопротивления намагничиванию, связанный с магнитным путем через ротор. Он определяет, какая часть нагрева с потерями железа относится к тепловому порту HR ротора, а какая - к четырем тепловым портам обмотки.

Примеры модели

Однополярный шаговый двигатель с управлением

Использование блоков Unipolar Stepper Motor Driver и Unipolar Stepper Motor для реализации управляемого шагового двигателя с постоянным магнитом. Модель предусматривает два варианта контроллера: один для управления положением и один для управления скоростью. Для изменения типа контроллера щелкните правой кнопкой мыши по блоку Controller, выберите Variant- > Override using- > и выберите Position или Speed.

Усредненный режим однополярного шагового двигателя

Однополярный шаговый двигатель, моделирующий в режимах степпинга и усредненного моделирования. Целью усредненного режима является ускорение моделирования любых нагрузок, которые не вызывают проскальзывания. Чтобы избежать неправильной интерпретации результатов, шаговый двигатель имеет приблизительное обнаружение проскальзывания, которое может быть настроено для генерации предупреждения или ошибки.

Ссылки

[1] М. Бодсон, Ж. Н. Чиассон, Р. Т. Новотнак и Р. Б. Рековски. «Высокопроизводительное нелинейное управление обратной связью шагового двигателя постоянного магнита». IEEE Transactions on Control Systems Technology, том 1, № 1, март 1993 года.

[2] П. П. Акарнли. Stepping Motors: Руководство по современной теории и практике. Нью-Йорк: Перегрин, 1982.

[3] С. Е. Лышевски. Электромеханические системы, электрические машины и прикладная мехатроника. КПР, 1999 ГОД.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Шаговый двигатель | Привод однополярного шагового двигателя

Представлен в R2012b

Документация

Однополярный шаговый двигатель

Описание

Усредненный режим

Тепловые порты

Допущения и ограничения

Порты

Сохранение

A+ - Верхнее А-фазное электрическое соединение электрический

A0 - Соединение A-фазного центрального ответвления электрический

A- - Нижнее А-фазное электрическое соединение электрический

B+ - Верхнее B-фазное электрическое соединение электрический

B0 - Соединение B-фазного центрального ответвления электрический

B- - Нижнее B-фазное электрическое соединение электрический

C - Дело механический

R - Ротор механический

HA+ - Тепловой порт для обмотки между A + и A0 тепловой

HA- - Тепловой порт для обмотки между A- и A0 тепловой

HB+ - Тепловой порт для обмотки между B + и B0 тепловой

HB- - Тепловой порт для обмотки между B- и B0 тепловой

HR - Тепловой порт ротора тепловой

Параметры

Электрический крутящий момент

Simulation mode - Режим моделирования Stepping (по умолчанию) | Averaged

Vector of rotational speeds - Вектор скоростей вращения [0, 1000, 3000] rpm (по умолчанию)

Зависимости

Vector of maximum torque values - Вектор максимальных значений крутящего момента [2, 2, 1] N*m (по умолчанию)

Зависимости

Action on slipping - Действие при обнаружении проскальзывания none (по умолчанию) | warn | error

Зависимости

Approximate total load inertia - Приблизительная суммарная инерция нагрузки 1e-4 kg*m^2 (по умолчанию)

Зависимости

Maximum step rate command - Команда максимальной скорости шага 10 Hz (по умолчанию)

Зависимости

Half-winding resistance - Сопротивление полуобмотки 0.55 Ohm (по умолчанию)

Зависимости

Half-winding inductance - Индуктивность полуобмотки 1.5e-3 H (по умолчанию)

Зависимости

Motor torque constant - Постоянный крутящий момент двигателя 0.19 N*m/A (по умолчанию)

Зависимости

Detent torque - Момент фиксации 0 N*m (по умолчанию)

Зависимости

Magnetizing resistance - Сопротивление намагничиванию inf Ohm (по умолчанию) | положительный скаляр

Зависимости

Full step size - Полный размер шага 1.8 deg (по умолчанию)

Coefficient of coupling - Коэффициент сцепления для взаимной индуктивности 0 (по умолчанию)

Механический

Rotor inertia - Инерция ротора 4.5e-5 kg*m^2 (по умолчанию)

Rotor damping - Демпфирование ротора 8.0e-4 N*m/(rad/s) (по умолчанию)

Initial rotor speed - Начальная частота вращения ротора 0 rpm (по умолчанию)

Initial rotor angle - Начальный угол ротора 0 deg (по умолчанию)

Температурная зависимость

Resistance temperature coefficient - Температурный коэффициент сопротивления 3.93e-3 1/K (по умолчанию)

Зависимости

Measurement temperature - Температура измерения 25 degC (по умолчанию)

Vector of maximum torque values at second measurement temperature - Вектор максимальных значений крутящего момента при второй температуре измерения [1.7, 1.7, .85] N*m (по умолчанию)

Зависимости

Second measurement temperature - Температура второго измерения 125 degC (по умолчанию)

Зависимости

Stepping mode - Шаговый режим Full stepping (по умолчанию) | Half stepping

Зависимости

Тепловой порт

Half-winding thermal mass - Тепловая масса полуобмотки 100 J/K (по умолчанию)

Half-winding initial temperatures, [T_A+ T_A- T_B+ T_B-] - Начальные температуры полуобмотки [25, 25, 25, 25] degC (по умолчанию)

Rotor thermal mass - Тепловая масса ротора 50 J/K (по умолчанию)

Rotor initial temperature - Начальная температура ротора 25 degC (по умолчанию)

Percentage of magnetizing resistance associated with the rotor - Процент сопротивления намагничиванию, связанный с ротором 90 (по умолчанию)

Примеры модели

Однополярный шаговый двигатель с управлением

Усредненный режим однополярного шагового двигателя

Ссылки

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Документация Simscape Electrical

Поддержка

`A+` - Верхнее А-фазное электрическое соединение
электрический

`A0` - Соединение A-фазного центрального ответвления
электрический

`A-` - Нижнее А-фазное электрическое соединение
электрический

`B+` - Верхнее B-фазное электрическое соединение
электрический

`B0` - Соединение B-фазного центрального ответвления
электрический

`B-` - Нижнее B-фазное электрическое соединение
электрический

`C` - Дело
механический

`R` - Ротор
механический

`HA+` - Тепловой порт для обмотки между A + и A0
тепловой

`HA-` - Тепловой порт для обмотки между A- и A0
тепловой

`HB+` - Тепловой порт для обмотки между B + и B0
тепловой

`HB-` - Тепловой порт для обмотки между B- и B0
тепловой

`HR` - Тепловой порт ротора
тепловой

`Simulation mode` - Режим моделирования
`Stepping` (по умолчанию) | `Averaged`

`Vector of rotational speeds` - Вектор скоростей вращения
`[0, 1000, 3000]` `rpm` (по умолчанию)

`Vector of maximum torque values` - Вектор максимальных значений крутящего момента
`[2, 2, 1]` `N*m` (по умолчанию)

`Action on slipping` - Действие при обнаружении проскальзывания
`none` (по умолчанию) | `warn` | `error`

`Approximate total load inertia` - Приблизительная суммарная инерция нагрузки
`1e-4` `kg*m^2` (по умолчанию)

`Maximum step rate command` - Команда максимальной скорости шага
`10` `Hz` (по умолчанию)

`Half-winding resistance` - Сопротивление полуобмотки
`0.55` `Ohm` (по умолчанию)

`Half-winding inductance` - Индуктивность полуобмотки
`1.5e-3` `H` (по умолчанию)

`Motor torque constant` - Постоянный крутящий момент двигателя
`0.19` `N*m/A` (по умолчанию)

`Detent torque` - Момент фиксации
`0` `N*m` (по умолчанию)

`Magnetizing resistance` - Сопротивление намагничиванию
`inf` `Ohm` (по умолчанию) | положительный скаляр

`Full step size` - Полный размер шага
`1.8` `deg` (по умолчанию)

`Coefficient of coupling` - Коэффициент сцепления для взаимной индуктивности
`0` (по умолчанию)

`Rotor inertia` - Инерция ротора
`4.5e-5` `kg*m^2` (по умолчанию)

`Rotor damping` - Демпфирование ротора
`8.0e-4` `N*m/(rad/s)` (по умолчанию)

`Initial rotor speed` - Начальная частота вращения ротора
`0` `rpm` (по умолчанию)

`Initial rotor angle` - Начальный угол ротора
`0` `deg` (по умолчанию)

`Resistance temperature coefficient` - Температурный коэффициент сопротивления
`3.93e-3` `1/K` (по умолчанию)

`Measurement temperature` - Температура измерения
`25` `degC` (по умолчанию)

`Vector of maximum torque values at second measurement temperature` - Вектор максимальных значений крутящего момента при второй температуре измерения
`[1.7, 1.7, .85]` `N*m` (по умолчанию)

`Second measurement temperature` - Температура второго измерения
`125` `degC` (по умолчанию)

`Stepping mode` - Шаговый режим
`Full stepping` (по умолчанию) | `Half stepping`

`Half-winding thermal mass` - Тепловая масса полуобмотки
`100` `J/K` (по умолчанию)

`Half-winding initial temperatures, [T_A+ T_A- T_B+ T_B-]` - Начальные температуры полуобмотки
`[25, 25, 25, 25]` `degC` (по умолчанию)

`Rotor thermal mass` - Тепловая масса ротора
`50` `J/K` (по умолчанию)

`Rotor initial temperature` - Начальная температура ротора
`25` `degC` (по умолчанию)

`Percentage of magnetizing resistance associated with the rotor` - Процент сопротивления намагничиванию, связанный с ротором
`90` (по умолчанию)

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™