В этом примере показано, как настроить электропривод с помощью каскадной структуры управления.
На рисунке показан контур управления с обратной связью, который использует каскадную структуру управления. Внешний контур регулирования скорости действует медленнее, чем внутренний контур регулирования тока.
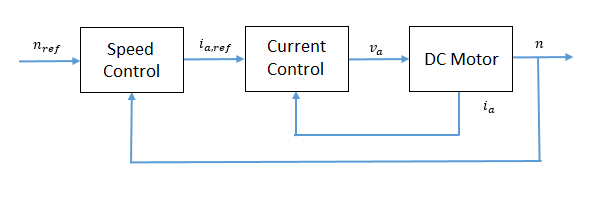
Для обеспечения требуемых контрольных характеристик для простой дискретной модели установки, Gf (z-1), используйте систему PI управления с замкнутым контуром GPI (z-1). Переходная производительность может быть выражена в терминах превышения. Перерасход уменьшается относительно коэффициента демпфирования:
где,
λ - переборка.
λ - коэффициент демпфирования.
Время отклика, tr, зависит от демпфирования и собственной частоты, λ n, так что:
Если ξ <0.7,
Если ξ ≥ 0.7,
Общий поток операций для проектирования PI-контроллера для системы первого заказа:
Дискретизируйте модель растения с помощью метода дискретизации с удержанием нулевого порядка (ZOH). То есть, учитывая, что уравнение первого порядка, представляющее растение,
+ 1,
где,
Km - это усиление первого порядка.
Tm - постоянная времени системы первого порядка.
Настройка
1z − 1Ts,
дает дискретную модель установки,
1 = b1z − 11 + a1z − 1,
whelTs - время выборки для контроллера дискретного времени.
Запишите представление дискретного времени для PI-контроллера с использованием того же преобразования. Для
(1 с),
настройка
1z − 1Ts,
дает модель дискретного контроллера,
1 = q0 + q1z − 11 − z − 1.
Объединение дискретных уравнений для установки и контроллера дает функцию передачи с замкнутым контуром для системы,
z − 1 + (− a1 + q1b1) z − 2,
Знаменателем передаточной функции является характеристический многочлен. То есть
+ (− a1 + q1b1) z − 2.
Характеристический многочлен для достижения требуемой производительности определяется как
1 + α2z − 2,
где,
ωnTs1 − α2).
2ξωnTs.
Чтобы определить параметры контроллера, установите характеристический многочлен для системы равным характеристическому многочлену для требуемой производительности. Если
(z − 1),
тогда
и
Решение для выходов q0 и q1
и
Следовательно, общие уравнения для пропорциональных и интегральных параметров управления для системы первого порядка
q0
и
KpTs.
Предполагая, что для системы в примерной модели, Kb = Kt, упрощенные математические уравнения для напряжения и крутящего момента двигателя постоянного тока являются
+ Кбом
и
= Kbia,
где:
va - напряжение якоря.
ia - ток якоря.
La - индуктивность якоря.
Ra - сопротивление якоря.
λ - угловая скорость ротора
Te - крутящий момент двигателя.
Нагрузка - это крутящий момент нагрузки.
Jm - момент инерции ротора.
Bmis - коэффициент вязкого трения.
Kb - константа пропорциональности.
Чтобы настроить контроллер тока, предположим, что модель является линейной, то есть обратная электродвижущая сила, представленная Kb, ничтожна. Это предположение допускает аппроксимацию модели растения с использованием уравнения Лапласа первого порядка:
s + 1.
С учетом системных требований теперь можно решать для КП и КИ. Требования к текущему контроллеру в примерной модели:
Время выборки, Ts = 1 мс.
Перестрелка, λ = 5%.
Время отклика, tr = 0,11 с.
Поэтому пропорциональными и интегральными параметрами для текущего контроллера являются:
7,7099.
455,1491.
Чтобы настроить регулятор скорости, аппроксимируйте модель установки простой моделью. Сначала предположим, что внутренний контур намного быстрее, чем внешний контур. Также предположим, что стационарная ошибка отсутствует. Эти допущения позволяют использовать систему первого порядка, рассматривая передаточную функцию 1 для внутреннего контура тока.
Для вывода скорости вращения в оборотах в минуту передаточная функция умножается на коэффициент 30/δ. Чтобы принять за управляющий вход ток якоря вместо крутящего момента двигателя, передаточная функция умножается на константу пропорциональности, Kb. Результатом аппроксимации для модели установки с внешним контуром является
с + 1.
Контроллер скорости имеет то же время выборки и требования к превышению, что и текущий контроллер, но время отклика медленнее, так что:
Время выборки Ts = 1 мс.
Перестрелка λ = 5%.
Время отклика tr = 0,50 с.
Поэтому пропорциональными и интегральными параметрами для регулятора скорости являются:
0,0045
0,0405
Изучите компоненты двигателя постоянного тока и каскадного контроллера.
Откройте модель. В командной строке MATLAB ® введите
model = 'ee_dc_motor_control'
open_system(model)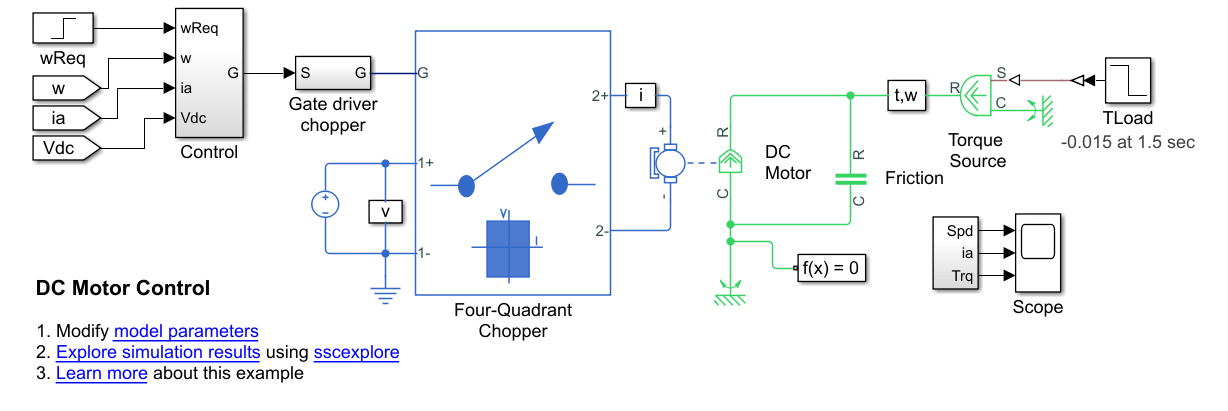
Подсистема управления содержит модель каскадной системы управления, построенной с использованием блоков из библиотеки Simulink ®.
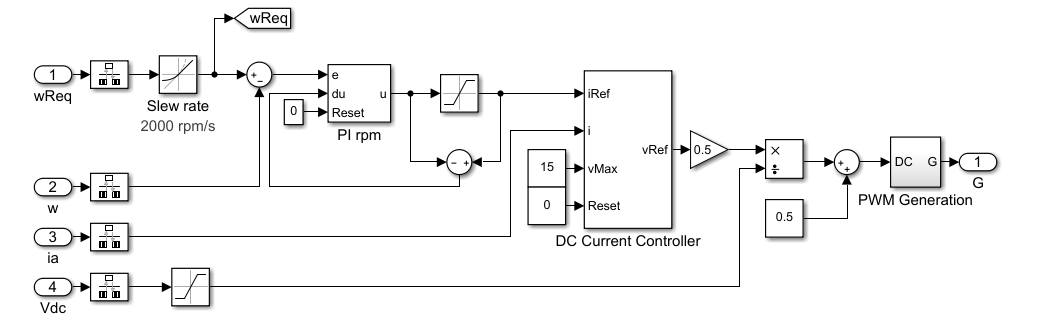
Блок четырехквадрантного прерывателя представляет четырехквадрантный прерыватель постоянного тока, который содержит два ответвления моста, каждое из которых имеет два блока IGBT (Ideal, Switching). Когда входное напряжение превышает пороговое значение 0.5 V, блоки IGBT (Ideal, Switching) ведут себя как линейные диоды с прямым напряжением 0.8 V и сопротивление 1e-4 Ом. Когда пороговое напряжение не превышено, блоки IGBT (Ideal, Switching) действуют как линейные резисторы с проводимостью в выключенном состоянии 1e-5 1/Ом.
Моделирование модели.
sim(model)
Просмотр результатов. Откройте блок «Область».
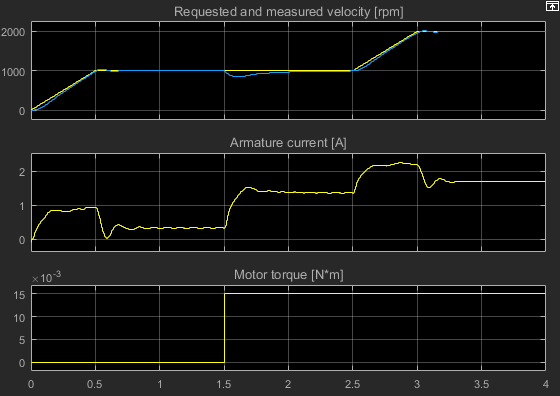
Через 1,5 секунды возникает крутящий момент нагрузки, который приводит к установившейся ошибке.
Настройте контроллер двигателя постоянного тока. ee_getDCMotorFirstOrderPIParams В этом примере функция вычисляет пропорциональный коэффициент усиления KP и интегральный коэффициент усиления KI для системы первого порядка.
Синтаксис функции: [Kp, Ki] = getParamPI(Km,Tm,Ts,sigma,tr).
Входными аргументами для функции являются системные параметры и требования к контроллеру:
Km - коэффициент усиления первого порядка.
Tm - постоянная времени системы первого порядка.
Ts - время выборки для контроллера дискретного времени.
sigma является желаемым максимальным превышением, λ.
tr - требуемое время отклика.
Для проверки уравнений в функции введите
edit ee_getDCMotorFirstOrderPIParamsЧтобы рассчитать параметры контроллера с помощью функции, сохраните эти системные параметры в рабочей области:
Ra=4.67; % [Ohm] La=170e-3; % [H] Bm=47.3e-6; % [N*m/(rad/s)] Jm=42.6e-6; % [Kg*m^2] Kb=14.7e-3; % [V/(rad/s)] Tsc=1e-3; % [s]
Рассчитайте параметры настройки текущего контроллера как функцию параметров и требований к внутреннему контроллеру:
Km = 1/Ra.
Tm = La/Ra.
Ts = Tsc.
sigma = 0.05.
Tr = 0.11.
[Kp_i, Ki_i] = ee_getDCMotorFirstOrderPIParams(1/Ra,La/Ra,Tsc,0.05,0.11)
Kp_i =
7.7099
Ki_i =
455.1491Параметры усиления для текущего контроллера сохраняются в рабочей области.
Рассчитайте параметры настройки контроллера скорости на основе параметров и требований к внешнему контроллеру:
Km = Kb*(30/pi).
Tm = Jm/Ra.
Ts = Tsc.
sigma = 0.05.
Tr = 0.5.
[Kp_n, Ki_n] = ee_getDCMotorFirstOrderPIParams((Kb*(30/pi))/Bm,Jm/Bm,Tsc,0.05,0.5)
Kp_n =
0.0045
Ki_n =
0.0405Параметры усиления для контроллера скорости сохраняются в рабочей области.
Моделирование модели с использованием сохраненных параметров усиления для скорости и контроллеров.
sim(model)
Просмотр результатов. Откройте блок «Область».
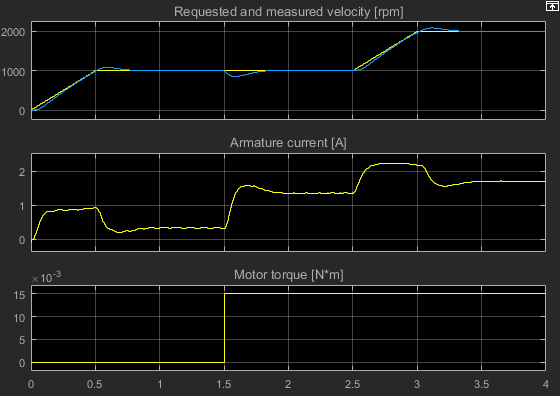
Перерасход немного больше, однако контроллер реагирует на изменение крутящего момента нагрузки гораздо быстрее.
Инерция | Вращательный электромеханический преобразователь | Вращательное трение