кватернион

Создание массива кватернионов

Описание

Кватернион - четырёхчастное гиперкомплексное число, используемое в трёхмерных вращениях и ориентациях.

Кватернионное число представлено в виде $a + bi +$ cj + dk, где a, b, c и d части - вещественные числа, а i, j и k - базисные элементы, удовлетворяющие ^{уравнению}: ⁱ² = ^j2 = k2 = ijk = − 1.

Множество кватернионов, обозначаемое H, определяется в четырёхмерном векторном пространстве над вещественными числами, R4. Каждый элемент H имеет уникальное представление, основанное на линейной комбинации базисных элементов, i, j и k.

Все вращения в 3-D могут быть описаны осью вращения и углом вокруг этой оси. Преимущество кватернионов над матрицами вращения состоит в том, что ось и угол поворота легко интерпретировать. Например, рассмотрим точку в R3. Для поворота точки задаются ось вращения и угол поворота.

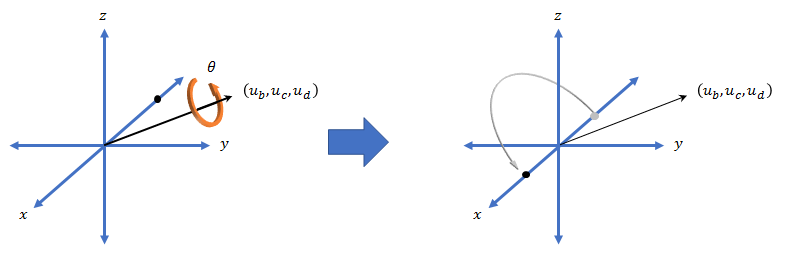
Кватернионное представление вращения может быть выражено как $q = \frac{\cos}{} (« 2») + \frac{}{} sin_{(«} 2»)_{} («_{ubi»} + «$ ucj» + «udk»), где

Создание

Синтаксис

quat = кватернион ()

quat = кватернион (A, B, C, D)

quat = кватернион (матрица)

quat = кватернион (RV, 'rotvec')

quat = кватернион (RV, 'rotvecd')

quat = кватернион (RM, 'rotmat', PF)

quat = кватернион (E, 'euler', RS, PF)

quat = кватернион (E, 'eulerd', RS, PF)

Описание

пример

quat = quaternion() создает пустой кватернион.

пример

quat = quaternion(A,B,C,D) создает массив кватернионов, в котором четыре части кватернионов взяты из массивов A, B, C, и D. Все входные данные должны иметь одинаковый размер и быть одного типа данных.

пример

quat = quaternion(matrix) создает массив N-by-1 кватерниона из матрицы N-by-4, где каждый столбец становится одной частью кватерниона.

пример

quat = quaternion(RV,'rotvec') создает множество кватерниона N-1 из матрицы N-3 векторов вращения, RV. Каждая строка RV представляет вектор вращения в радианах.

пример

quat = quaternion(RV,'rotvecd') создает множество кватерниона N-1 из матрицы N-3 векторов вращения, RV. Каждая строка RV представляет вектор поворота в градусах.

пример

quat = quaternion(RM,'rotmat',PF) создает множество кватерниона N-1 из множества матриц вращения 3 на 3 на Н, RM. PF может быть либо 'point' если углы Эйлера представляют повороты точек или 'frame' для поворота рамы.

пример

quat = quaternion(E,'euler',RS,PF) создает множество кватерниона N-1 из матрицы N-3, E. Каждая строка E представляет набор углов Эйлера в радианах. Углы в E - последовательные повороты вокруг осей RS.

пример

quat = quaternion(E,'eulerd',RS,PF) создает множество кватерниона N-1 из матрицы N-3, E. Каждая строка E представляет набор углов Эйлера в градусах. Углы в E - последовательные повороты вокруг осей RS.

Входные аргументы

развернуть все

`A,B,C,D` - Части кватерниона
массивы одного размера, разделенные запятыми

Части кватерниона, определяемые как четыре разделенных запятыми скаляра, матрицы или многомерные массивы одинакового размера.

Пример: quat = quaternion(1,2,3,4) создает кватернион вида 1 + 2i + 3j + 4k.

Пример: quat = quaternion([1,5],[2,6],[3,7],[4,8]) создает массив кватернионов 1 на 2, где quat(1,1) = 1 + 2i + 3j + 4k и quat(1,2) = 5 + 6i + 7j + 8k

Типы данных: single | double

`matrix` - Матрица частей кватерниона
N-by-4 матрица

Матрица частей кватерниона, заданная как матрица N-by-4. Каждая строка представляет отдельный кватернион. Каждый столбец представляет отдельную часть кватерниона.

Пример: quat = quaternion(rand(10,4)) создает массив кватернионов 10 на 1.

Типы данных: single | double

`RV` - Матрица векторов вращения
N-by-3 матрица

Матрица векторов вращения, заданная как N-by-3 матрица. Каждая строка RV представляет элементы [X Y Z] вектора вращения. Вектор вращения - это единичный вектор, представляющий ось вращения, масштабированную на угол поворота в радианах или градусах.

Чтобы использовать этот синтаксис, укажите первый аргумент в качестве матрицы векторов вращения и второй аргумент в качестве 'rotvec' или 'rotvecd'.

Пример: quat = quaternion(rand(10,3),'rotvec') создает массив кватернионов 10 на 1.

Типы данных: single | double

`RM` - Матрицы вращения
матрица 3 на 3 | массив 3-by-3-by-N

Массив матриц вращения, задаваемый матрицей 3 на 3 или массивом 3-by-3-by-N. Каждая страница массива представляет отдельную матрицу поворота.

Пример: quat = quaternion(rand(3),'rotmat','point')

Пример: quat = quaternion(rand(3),'rotmat','frame')

Типы данных: single | double

`PF` - Тип матрицы вращения
`'point'` | `'frame'`

Тип матрицы вращения, указанный 'point' или 'frame'.

Пример: quat = quaternion(rand(3),'rotmat','point')

Пример: quat = quaternion(rand(3),'rotmat','frame')

Типы данных: char | string

`E` - Матрица углов Эйлера
N-by-3 матрица

Матрица углов Эйлера, заданная матрицей N-by-3. При использовании 'euler' синтаксис, укажите E в радианах. При использовании 'eulerd' синтаксис, укажите E в градусах.

Пример: quat = quaternion(E,'euler','YZY','point')

Пример: quat = quaternion(E,'euler','XYZ','frame')

Типы данных: single | double

`RS` - Последовательность вращения
символьный вектор | скалярная строка

Последовательность поворота, заданная как трехэлементный символьный вектор:

'YZY'
'YXY'
'ZYZ'
'ZXZ'
'XYX'
'XZX'
'XYZ'
'YZX'
'ZXY'
'XZY'
'ZYX'
'YXZ'

Предположим, что необходимо определить новые координаты точки при повороте ее системы координат с помощью поворота рамки. Точка определяется в исходной системе координат следующим образом:

point = [sqrt(2)/2,sqrt(2)/2,0];

В этом представлении первый столбец представляет ось X, второй столбец представляет ось Y, а третий столбец представляет ось Z.

Требуется повернуть точку с помощью представления угла Эйлера [45,45,0]. Поверните точку, используя две различные последовательности поворота:

При создании кватернионного вращателя и задании последовательности «ZYX» рамка сначала поворачивается на 45 ° вокруг оси Z, а затем на 45 ° вокруг новой оси Y.
```
quatRotator = quaternion([45,45,0],'eulerd','ZYX','frame');
newPointCoordinate = rotateframe(quatRotator,point)
```
```
newPointCoordinate =

    0.7071   -0.0000    0.7071
```
При создании кватернионного вращателя и задании последовательности YZX рамка сначала поворачивается на 45 ° вокруг оси Y, а затем на 45 ° вокруг новой оси Z.
```
quatRotator = quaternion([45,45,0],'eulerd','YZX','frame');
newPointCoordinate = rotateframe(quatRotator,point)
```
```
newPointCoordinate =

    0.8536    0.1464    0.5000
```

Типы данных: char | string

Функции объекта

`angvel`	Угловая скорость из массива кватернионов
`classUnderlying`	Класс деталей в кватернионе
`compact`	Преобразование массива кватернионов в матрицу N-by-4
`conj`	Комплексный конъюгат кватерниона
`ctranspose, '`	Комплексное сопряженное транспонирование массива кватернионов
`dist`	Угловое расстояние в радианах
`euler`	Перевести кватернион в углы Эйлера (радианы)
`eulerd`	Преобразовать кватернион в углы Эйлера (градусы)
`exp`	Экспонента массива кватернионов
`ldivide, .\`	Деление левого кватерниона по элементам
`log`	Натуральный логарифм массива кватернионов
`meanrot`	Среднее вращение кватерниона
`minus, -`	Вычитание кватерниона
`mtimes, *`	Умножение кватерниона
`norm`	Норма кватерниона
`normalize`	Нормализация кватерниона
`ones`	Создание массива кватернионов с вещественными деталями, равными единице, и мнимыми деталями, равными нулю
`parts`	Извлечь части кватерниона
`power, .^`	Мощность кватерниона по элементам
`prod`	Произведение массива кватернионов
`randrot`	Равномерно распределенные случайные повороты
`rdivide, ./`	Правое деление кватерниона по элементам
`rotateframe`	Поворот кадра кватерниона
`rotatepoint`	Поворот точки кватерниона
`rotmat`	Преобразование кватерниона в матрицу вращения
`rotvec`	Преобразовать кватернион в вектор вращения (радианы)
`rotvecd`	Преобразование кватерниона в вектор поворота (градусы)
`slerp`	Сферическая линейная интерполяция
`times, .*`	Элементное кватернионное умножение
`transpose, '`	Транспонировать массив кватернионов
`uminus, -`	Четвертичный унарный минус
`zeros`	Создание массива кватернионов с нулевым значением для всех деталей

Примеры

свернуть все

Создать пустую кватернион

Открыть сценарий в реальном времени

quat = quaternion()

quat = 

  0x0 empty quaternion array

По умолчанию базовый класс кватерниона является двойным.

classUnderlying(quat)

ans = 
'double'

Создание кватерниона путем задания отдельных деталей кватерниона

Открыть сценарий в реальном времени

Можно создать массив кватернионов, указав четыре части как разделенные запятыми скаляры, матрицы или многомерные массивы одинакового размера.

Определите части кватерниона как скаляры.

A = 1.1;
B = 2.1;
C = 3.1;
D = 4.1;
quatScalar = quaternion(A,B,C,D)

quatScalar = quaternion
     1.1 + 2.1i + 3.1j + 4.1k

Определите части кватерниона как векторы столбцов.

A = [1.1;1.2];
B = [2.1;2.2];
C = [3.1;3.2];
D = [4.1;4.2];
quatVector = quaternion(A,B,C,D)

quatVector=2×1 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k
     1.2 + 2.2i + 3.2j + 4.2k

Определите части кватерниона как матрицы.

A = [1.1,1.3; ...
     1.2,1.4];
B = [2.1,2.3; ...
     2.2,2.4];
C = [3.1,3.3; ...
     3.2,3.4];
D = [4.1,4.3; ...
     4.2,4.4];
quatMatrix = quaternion(A,B,C,D)

quatMatrix=2×2 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k     1.3 + 2.3i + 3.3j + 4.3k
     1.2 + 2.2i + 3.2j + 4.2k     1.4 + 2.4i + 3.4j + 4.4k

Определите части кватерниона как трехмерные массивы.

A = randn(2,2,2);
B = zeros(2,2,2);
C = zeros(2,2,2);
D = zeros(2,2,2);
quatMultiDimArray = quaternion(A,B,C,D)

quatMultiDimArray = 2x2x2 quaternion array
quatMultiDimArray(:,:,1) = 

     0.53767 +       0i +       0j +       0k     -2.2588 +       0i +       0j +       0k
      1.8339 +       0i +       0j +       0k     0.86217 +       0i +       0j +       0k


quatMultiDimArray(:,:,2) = 

     0.31877 +       0i +       0j +       0k    -0.43359 +       0i +       0j +       0k
     -1.3077 +       0i +       0j +       0k     0.34262 +       0i +       0j +       0k

Создание кватерниона путем задания матрицы деталей кватерниона

Открыть сценарий в реальном времени

Можно создать скалярный или столбчатый вектор кватернионов, указав N-by-4 матрицу кватернионных частей, где столбцы соответствуют кватернионным частям A, B, C и D.

Создайте вектор-столбец случайных кватернионов.

quatParts = rand(3,4)

quatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

quat = quaternion(quatParts)

quat=3×1 quaternion array
     0.81472 + 0.91338i +  0.2785j + 0.96489k
     0.90579 + 0.63236i + 0.54688j + 0.15761k
     0.12699 + 0.09754i + 0.95751j + 0.97059k

Чтобы получить quatParts матрица из представления кватерниона, использование compact.

retrievedquatParts = compact(quat)

retrievedquatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

Создание кватерниона путем задания векторов поворота

Открыть сценарий в реальном времени

Вы можете создать множество кватерниона N-1, определив матрицу N-3 векторов вращения в радианах или степенях. Векторы вращения - это компактные пространственные представления, которые имеют отношение один к одному с нормализованными кватернионами.

Векторы вращения в радианах

Создайте скалярный кватернион с помощью вектора поворота и убедитесь, что полученный кватернион нормализован.

rotationVector = [0.3491,0.6283,0.3491];
quat = quaternion(rotationVector,'rotvec')

quat = quaternion
     0.92124 + 0.16994i + 0.30586j + 0.16994k

norm(quat)

ans = 1.0000

Можно преобразовать из кватернионов в векторы вращения в радианах, используя rotvec функция. Восстановить rotationVector из кватерниона, quat.

rotvec(quat)

ans = 1×3

    0.3491    0.6283    0.3491

Векторы вращения в градусах

rotationVector = [20,36,20];
quat = quaternion(rotationVector,'rotvecd')

quat = quaternion
     0.92125 + 0.16993i + 0.30587j + 0.16993k

norm(quat)

ans = 1

Можно преобразовать из кватернионов в векторы вращения в градусах, используя rotvecd функция. Восстановить rotationVector из кватерниона, quat.

rotvecd(quat)

ans = 1×3

   20.0000   36.0000   20.0000

Создание кватерниона путем задания матриц вращения

Открыть сценарий в реальном времени

Можно создать N-by-1 массив кватернионов, указав 3-by-3-by-N массив матриц вращения. Каждая страница массива матрицы вращения соответствует одному элементу массива кватернионов.

Создайте скалярный кватернион с помощью матрицы вращения 3 на 3. Укажите, следует ли интерпретировать матрицу поворота как поворот рамки или точки.

rotationMatrix = [1 0         0; ...
                  0 sqrt(3)/2 0.5; ...
                  0 -0.5      sqrt(3)/2];
quat = quaternion(rotationMatrix,'rotmat','frame')

quat = quaternion
     0.96593 + 0.25882i +       0j +       0k

Можно преобразовать из кватернионов в матрицы вращения с помощью rotmat функция. Восстановить rotationMatrix из кватерниона, quat.

rotmat(quat,'frame')

ans = 3×3

    1.0000         0         0
         0    0.8660    0.5000
         0   -0.5000    0.8660

Создание кватерниона путем задания углов Эйлера

Открыть сценарий в реальном времени

Вы можете создать множество кватерниона N-1, определив множество N-3 углов Эйлера в радианах или степенях.

Эйлер Ракурс в Радианах

Используйте euler синтаксис для создания скалярного кватерниона с использованием вектора 1 на 3 углов Эйлера в радианах. Задайте последовательность поворота углов Эйлера и укажите, представляют ли углы поворот рамки или точки.

E = [pi/2,0,pi/4];
quat = quaternion(E,'euler','ZYX','frame')

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

Можно преобразовать из кватернионов в углы Эйлера с помощью euler функция. Восстановите углы Эйлера, E, из кватерниона, quat.

euler(quat,'ZYX','frame')

ans = 1×3

    1.5708         0    0.7854

Углы Эйлера в градусах

Используйте eulerd синтаксис для создания скалярного кватерниона с использованием вектора 1 на 3 углов Эйлера в градусах. Задайте последовательность поворота углов Эйлера и укажите, представляют ли углы поворот рамки или точки.

E = [90,0,45];
quat = quaternion(E,'eulerd','ZYX','frame')

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

Можно преобразовать из кватернионов в углы Эйлера в градусах с помощью eulerd функция. Восстановите углы Эйлера, E, из кватерниона, quat.

eulerd(quat,'ZYX','frame')

ans = 1×3

   90.0000         0   45.0000

Алгебра Кватерниона

Открыть сценарий в реальном времени

Кватернионы образуют некоммутативную ассоциативную алгебру над вещественными числами. Этот пример иллюстрирует правила алгебры кватернионов.

Сложение и вычитание

Сложение и вычитание кватернионов происходит по частям и являются коммутативными:

Q1 = quaternion(1,2,3,4)

Q1 = quaternion
     1 + 2i + 3j + 4k

Q2 = quaternion(9,8,7,6)

Q2 = quaternion
     9 + 8i + 7j + 6k

Q1plusQ2 = Q1 + Q2

Q1plusQ2 = quaternion
     10 + 10i + 10j + 10k

Q2plusQ1 = Q2 + Q1

Q2plusQ1 = quaternion
     10 + 10i + 10j + 10k

Q1minusQ2 = Q1 - Q2

Q1minusQ2 = quaternion
    -8 - 6i - 4j - 2k

Q2minusQ1 = Q2 - Q1

Q2minusQ1 = quaternion
     8 + 6i + 4j + 2k

Можно также выполнить сложение и вычитание вещественных чисел и кватернионов. Первая часть кватерниона называется действительной частью, в то время как вторая, третья и четвертая части называются вектором. Сложение и вычитание с вещественными числами влияют только на действительную часть кватерниона.

Q1plusRealNumber = Q1 + 5

Q1plusRealNumber = quaternion
     6 + 2i + 3j + 4k

Q1minusRealNumber = Q1 - 5

Q1minusRealNumber = quaternion
    -4 + 2i + 3j + 4k

Умножение

Умножение кватерниона определяется произведениями базисных элементов и распределительного закона. Напомним, что умножение базисных элементов, i, j и k, не являются коммутативными, и поэтому кватернионное умножение не является коммутативным.

Q1timesQ2 = Q1 * Q2

Q1timesQ2 = quaternion
    -52 + 16i + 54j + 32k

Q2timesQ1 = Q2 * Q1

Q2timesQ1 = quaternion
    -52 + 36i + 14j + 52k

isequal(Q1timesQ2,Q2timesQ1)

ans = logical
   0

Можно также умножить кватернион на вещественное число. Если умножить кватернион на вещественное число, каждая часть кватерниона умножается на вещественное число по отдельности:

Q1times5 = Q1*5

Q1times5 = quaternion
      5 + 10i + 15j + 20k

Умножение кватерниона на вещественное число коммутативно.

isequal(Q1*5,5*Q1)

ans = logical
   1

Спряжение

Комплексный конъюгат кватерниона определяется так, что каждый элемент векторной части кватерниона отрицается.

Q1

Q1 = quaternion
     1 + 2i + 3j + 4k

conj(Q1)

ans = quaternion
     1 - 2i - 3j - 4k

Умножение между кватернионом и его конъюгатом коммутативно:

isequal(Q1*conj(Q1),conj(Q1)*Q1)

ans = logical
   1

Манипуляция массивом кватерниона

Открыть сценарий в реальном времени

Кватернионы можно упорядочить в векторы, матрицы и многомерные массивы. Встроенные функции MATLAB ® были расширены для работы с кватернионами.

Связать

Кватернионы обрабатываются как отдельные объекты во время конкатенации и следуют правилам MATLAB для манипулирования массивом.

Q1 = quaternion(1,2,3,4);
Q2 = quaternion(9,8,7,6);

qVector = [Q1,Q2]

qVector=1×2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k

Q3 = quaternion(-1,-2,-3,-4);
Q4 = quaternion(-9,-8,-7,-6);

qMatrix = [qVector;Q3,Q4]

qMatrix=2×2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMultiDimensionalArray(:,:,1) = qMatrix;
qMultiDimensionalArray(:,:,2) = qMatrix

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Индексация

Чтобы получить доступ или назначить элементы в массиве кватерниона, используйте индексирование.

qLoc2 = qMultiDimensionalArray(2)

qLoc2 = quaternion
    -1 - 2i - 3j - 4k

Замените кватернион с индексом два на кватернион один.

qMultiDimensionalArray(2) = ones('quaternion')

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Измениться

Чтобы изменить форму массивов кватернионов, используйте reshape функция.

qMatReshaped = reshape(qMatrix,4,1)

qMatReshaped=4×1 quaternion array
     1 + 2i + 3j + 4k
    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k
    -9 - 8i - 7j - 6k

Переместить

Для транспонирования векторов кватернионов и матриц используйте transpose функция.

qMatTransposed = transpose(qMatrix)

qMatTransposed=2×2 quaternion array
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Переставить

Для перестановки векторов кватернионов, матриц и многомерных массивов используйте permute функция.

qMultiDimensionalArray

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMatPermute = permute(qMultiDimensionalArray,[3,1,2])

qMatPermute = 2x2x2 quaternion array
qMatPermute(:,:,1) = 

     1 + 2i + 3j + 4k     1 + 0i + 0j + 0k
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k


qMatPermute(:,:,2) = 

     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™

Представлен в R2021a

Документация

кватернион

Описание

Создание

Синтаксис

Описание

Входные аргументы

`A,B,C,D` - Части кватерниона
массивы одного размера, разделенные запятыми

`matrix` - Матрица частей кватерниона
N-by-4 матрица

`RV` - Матрица векторов вращения
N-by-3 матрица

`RM` - Матрицы вращения
матрица 3 на 3 | массив 3-by-3-by-N

`PF` - Тип матрицы вращения
`'point'` | `'frame'`

`E` - Матрица углов Эйлера
N-by-3 матрица

`RS` - Последовательность вращения
символьный вектор | скалярная строка

Функции объекта

Примеры

Создать пустую кватернион

Создание кватерниона путем задания отдельных деталей кватерниона

Создание кватерниона путем задания матрицы деталей кватерниона

Создание кватерниона путем задания векторов поворота

Создание кватерниона путем задания матриц вращения

Создание кватерниона путем задания углов Эйлера

Алгебра Кватерниона

Манипуляция массивом кватерниона

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™

Документация по панели инструментов радара

Поддержка

Документация

кватернион

Описание

Создание

Синтаксис

Описание

Входные аргументы

A,B,C,D - Части кватерниона массивы одного размера, разделенные запятыми

matrix - Матрица частей кватерниона N-by-4 матрица

RV - Матрица векторов вращения N-by-3 матрица

RM - Матрицы вращения матрица 3 на 3 | массив 3-by-3-by-N

PF - Тип матрицы вращения 'point' | 'frame'

E - Матрица углов Эйлера N-by-3 матрица

RS - Последовательность вращения символьный вектор | скалярная строка

Функции объекта

Примеры

Создать пустую кватернион

Создание кватерниона путем задания отдельных деталей кватерниона

Создание кватерниона путем задания матрицы деталей кватерниона

Создание кватерниона путем задания векторов поворота

Создание кватерниона путем задания матриц вращения

Создание кватерниона путем задания углов Эйлера

Алгебра Кватерниона

Манипуляция массивом кватерниона

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью MATLAB ® Coder™

Документация по панели инструментов радара

Поддержка

`A,B,C,D` - Части кватерниона
массивы одного размера, разделенные запятыми

`matrix` - Матрица частей кватерниона
N-by-4 матрица

`RV` - Матрица векторов вращения
N-by-3 матрица

`RM` - Матрицы вращения
матрица 3 на 3 | массив 3-by-3-by-N

`PF` - Тип матрицы вращения
`'point'` | `'frame'`

`E` - Матрица углов Эйлера
N-by-3 матрица

`RS` - Последовательность вращения
символьный вектор | скалярная строка

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™