Exponenta Banner
exponenta event banner

Обратная кинематика

Вычислить конфигурации соединений для достижения положения «конец-эффектор»

развернуть все на странице
  • Библиотека:

  • Инструментарий робототехнической системы/Алгоритмы манипуляторов

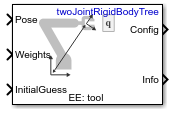
  • Inverse Kinematics block

Описание

Блок «Обратная кинематика» (Inverse Kinematics) использует решатель обратной кинематики (IK) для вычисления конфигураций соединений для требуемой позы конечного эффектора на основе заданной модели дерева жесткого тела. Создайте модель дерева жесткого тела для робота с помощью rigidBodyTree класс. Модель дерева жесткого тела определяет все ограничения соединения, которые применяются решателем.

Укажите RigidBodyTree параметр и требуемый конечный эффектор внутри блочной маски. Параметры алгоритма также можно настроить на вкладке Параметры решателя (Solver Parameters).

Введите требуемый конечный эффектор Поза (Pose), Весы для допуска позы (Weights on pose tolerance) и InitityGuess для конфигурации соединения. Решатель выводит конфигурацию робота «Конфигурация» (Config), которая удовлетворяет позе конечного эффектора в пределах допусков, заданных на вкладке Параметры решателя (Solver Parameters).

Порты

Вход

развернуть все

Концевая эффекторная поза, заданная как однородное преобразование 4 на 4. Это преобразование определяет требуемое положение и ориентацию жесткого тела, указанного в параметре End effector.

Типы данных: single | double

Веса для допусков позы, указанные как шестиэлементный вектор. Первые три элемента вектора соответствуют весам на погрешности ориентации для нужной позы. Последние три элемента вектора соответствуют весам ошибки в положении xyz для требуемой позы.

Типы данных: single | double

Начальное предположение о конфигурации робота, определяемое как вектор положений соединения. Количество положений равно количеству нефиксированных соединений в параметре Дерево жесткого тела (Rigid body tree). Используйте это начальное предположение, чтобы помочь определить нужную конфигурацию робота. Однако решение не гарантировано близким к этому первоначальному предположению.

Типы данных: single | double

Продукция

развернуть все

Конфигурация робота, которая решает требуемую конечную эффекторную позу, заданную как вектор. Конфигурация робота - это вектор положений соединения для модели дерева жесткого тела. Количество положений равно количеству нефиксированных соединений в параметре Дерево жесткого тела (Rigid body tree).

Типы данных: single | double

Информация о решении, возвращаемая в виде шины. Шина информации о решении содержит следующие элементы:

  • Iterations - количество итераций, выполняемых алгоритмом.

  • PoseErrorNorm - Величина ошибки между позой концевого эффектора в растворе и желаемой позой концевого эффектора.

  • ExitFlag - Код, который дает более подробную информацию о выполнении алгоритма и о том, что заставило его вернуться. Флаги выхода каждого типа алгоритма см. в разделе Флаги выхода.

  • Status - символьный вектор, описывающий, находится ли решение в пределах допуска (1) или является наилучшим возможным решением, которое может найти алгоритм (2).

Параметры

развернуть все

Параметры блока

Модель дерева жесткого тела, заданная как rigidBodyTree объект. Создайте модель робота в рабочем пространстве MATLAB ® перед заданием в маске блока.

Имя конечного эффектора для требуемой позы. Чтобы увидеть список тел на rigidBodyTree укажите параметр дерева «Жесткое тело» и нажмите кнопку «Выбрать тело».

Выберите, чтобы включить порт Info и получить диагностическую информацию для решения решателя.

Параметры решателя

Алгоритм решения обратной кинематики, указанный как 'BFGSGradientProjection' или 'LevenbergMarquardt'. Подробные сведения о каждом алгоритме см. в разделе Алгоритмы обратной кинематики.

Выберите этот параметр, чтобы применить пределы соединения, указанные в модели дерева жесткого тела.

Максимальное число итераций для оптимизации решения, указанное как положительное целое число. Увеличение числа итераций может улучшить решение за счет времени выполнения.

Максимальное количество секунд, в течение которых алгоритм работает до истечения времени ожидания, указанное как положительный скаляр. Увеличение максимального времени может улучшить решение за счет времени выполнения.

Порог градиента функции затрат, заданный как положительный скаляр. Алгоритм останавливается, если величина градиента падает ниже этого порога. Низкая величина градиента обычно указывает на то, что решатель сходится к решению.

Порог величины ошибки между конечной эффекторной позой, генерируемой из решения, и требуемой позой, определяемой как положительный скаляр. Weights указанные для каждого компонента позы включаются в этот расчет.

Минимальный размер шага, допустимый решателем, указанный как положительный скаляр. Меньшие размеры шага обычно означают, что решение близко к сходимости.

Порог изменения ошибки позы конечного эффектора между итерациями, заданный как положительный скаляр. Алгоритм возвращает, если изменения во всех элементах ошибки позы меньше этого порога.

Зависимости

Этот параметр включается, когда решатель Levenberg-Marquadt.

Установите флажок, чтобы включить демпфирование ошибок, и укажите Damping bias параметр.

Зависимости

Этот параметр включается, когда решатель Levenberg-Marquadt.

Демпфирование функции затрат, заданной как положительный скаляр. Алгоритм Левенберга-Марквадта имеет функцию демпфирования, управляемую этим скаляром, который работает с функцией затрат для управления скоростью сходимости.

Зависимости

Этот параметр включается, когда решатель Levenberg-Marquadt и Использовать демпфирование ошибок on.

  • Interpreted execution - Моделирование модели с помощью интерпретатора MATLAB. Эта опция сокращает время запуска, но имеет более низкую скорость моделирования, чем Code generation. В этом режиме можно отладить исходный код блока.

  • Code generation - Моделирование модели с использованием сгенерированного кода C. При первом запуске моделирования Simulink ® генерирует код C для блока. Код C используется повторно для последующего моделирования, если модель не изменяется. Эта опция требует дополнительного времени запуска, но скорость последующего моделирования сравнима сInterpreted execution.

Настраиваемый: Нет

Примеры модели

Trace An End-Effector Trajectory with Inverse Kinematics in Simulink

Трассировка конечной эффекторной траектории с обратной кинематикой в Simulink

Используйте модель робота жесткого тела для вычисления обратной кинематики с помощью Simulink ®. Определите траекторию для концевого эффектора робота и закольцовывайте точки для решения конфигураций робота, которые отслеживают эту траекторию.

Ссылки

[1] Бадреддин, Хасан, Стефан Вандевалле и Йохан Мейерс. «Последовательное квадратичное программирование (SQP) для оптимального управления при прямом численном моделировании турбулентного потока». Журнал вычислительной физики. 256 (2014): 1–16. doi: 10.1016/j.jcp.2013.08.044.

[2] Берцекас, Дмитрий П. Нелинейное программирование. Belmont, MA: Athena Scientific, 1999.

[3] Голдфарб, Дональд. «Расширение метода переменной метрики Давидона до максимизации при линейном неравенстве и ограничениях равенства». Журнал СИАМ по прикладной математике. т. 17, № 4 (1969): 739-64. дои: 10.1137/0117067.

[4] Нокедал, Хорхе и Стивен Райт. Численная оптимизация. Нью-Йорк, Нью-Йорк: Спрингер, 2006.

[5] Сугихара, Томомичи. «Разрешимость - бесконтрольная обратная кинематика методом Левенберга-Марквардта». Транзакции IEEE по робототехнике. т. 27, № 5 (2011): 984-91. дои: 10.1109/tro.2011.2148230.

[6] Чжао, Цзяньминь и Норман И. Бадлер. «Обратное кинематическое позиционирование с использованием нелинейного программирования для высокоартикулированных фигур». Транзакции ACM на графике. Том 13, № 4 (1994): 313-36. дои: 10,1145/ 195826,195827.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

.

См. также

Объекты

Блоки

Темы

Представлен в R2018b

Документация по инструментам робототехнической системы

Поддержка