Exponenta Banner
exponenta event banner

lftdata

Разложение неопределенных объектов на фиксированные определенные и нормализованные неопределенные части

свернуть все на странице

Синтаксис

[M,Delta] = lftdata(A);
[M,Delta] = lftdata(A,List);
[M,Delta,Blkstruct] = lftdata(A);
[M,Delta,Blkstruct,Normunc] = lftdata(A);

Описание

lftdata разлагает неопределенный объект на фиксированную определенную часть и нормализованную неопределенную часть. lftdata может также частично разложить неопределенный объект на неопределенную часть и нормализованную неопределенную часть. Неопределенные объекты (umat, ufrd, uss) представлены как определенные (т.е. не неопределенные) объекты в обратной связи с блок-диагональными конкатенациями неопределенных элементов.

[M,Delta] = lftdata(A) отделяет неопределенный объект A в определенный объект M и нормализованная неопределенная матрица Delta такой, что A равно lft(Delta,M), как показано ниже.

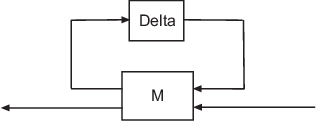
Если A является umat, то M будет double; если A является uss, то M будет ss; если A является ufrd, то M будет frd. Во всех случаях: Delta является umat.

[M,Delta] = lftdata(A,List) отделяет неопределенный объект A в неопределенный объект M, в обратной связи с нормализованной неопределенной матрицей Delta. List является массивом ячеек (или символов) имен неопределенных элементов A которые составляют Delta. Вся другая неопределенность в A остается в M.

lftdata(A,fieldnames(A.Uncertainty)) является таким же, как lftdata(A).

[M,DELTA,BLKSTRUCT] = lftdata(A) возвращает массив структуры N-by-1 BLKSTRUCT, где BLKSTRUCT(i) описывает i-й нормализованный неопределенный элемент. Это описание неопределенности может быть передано непосредственно в низкоуровневую структурированную функцию анализа сингулярных значений. mussv.

[M,DELTA,BLKSTRUCT,NORMUNC] = lftdata(A) возвращает массив ячеек NORMUNC нормированных неопределенных элементов. Каждый нормализованный элемент имеет 'Normalized' добавил к своему первоначальному названию, чтобы избежать путаницы. Обратите внимание, что lft(blkdiag(NORMUNC{:}),M) эквивалентно A. Нормализация для каждого типа неопределенного элемента описана в разделе Декомпозиция неопределенных объектов.

Примеры

свернуть все

Открыть сценарий в реальном времени

Создание неопределенной матрицы A с неопределенными параметрами p1, и p2. Разложиться A в свою определенную часть, Mи нормализованная неопределенная часть, Delta.

p1 = ureal('p1',-3,'perc',40); 
p2 = ucomplex('p2',2); 
A = [p1 p1+p2;1 p2]; 
[M,Delta] = lftdata(A);

Можно проверить разницу между исходной неопределенной матрицей, Aи результат, полученный путем объединения двух результатов разложения.

simplify(A-lft(Delta,M)) 
ans = 2×2

     0     0
     0     0


M
M = 4×4

         0         0    1.0954    1.0954
         0         0         0    1.0000
    1.0954    1.0000   -3.0000   -1.0000
         0    1.0000    1.0000    2.0000

Проверить наихудшую норму неопределенной детали можно с помощью wcnorm. Сравнение образцов неопределенной части A с неопределенной матрицей A.

wcn = wcnorm(Delta) 
wcn = struct with fields:
    LowerBound: 0
    UpperBound: 1.0012


usample(Delta,3) 
ans = 
ans(:,:,1) =

   0.6294 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.8776 - 0.4413i


ans(:,:,2) =

   0.8116 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.2704 + 0.2907i


ans(:,:,3) =

  -0.7460 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i  -0.3382 + 0.9253i
Открыть сценарий в реальном времени

Создание неопределенной матрицы A с 2 неопределенными реальными параметрами v1 и v2. Создание неопределенной системы G использование A в качестве динамической матрицы и числовых матриц для ввода и вывода.

A = [ureal('p1',-3,'perc',40) 1;1 ureal('p2',-2)]; 
sys = ss(A,[1;0],[0 1],0);
sys.InputGroup.ActualIn = 1; 
sys.OutputGroup.ActualOut = 1;

Можно разложить G в определенную систему, Msysи нормализованную неопределенную матрицу, Delta. Вы можете видеть из Msys это несомненно, и что входные и выходные группы были скорректированы.

[Msys,Delta] = lftdata(sys); 
Msys 
Msys =
 
  A = 
       x1  x2
   x1  -3   1
   x2   1  -2
 
  B = 
          u1     u2     u3
   x1  1.095      0      1
   x2      0      1      0
 
  C = 
          x1     x2
   y1  1.095      0
   y2      0      1
   y3      0      1
 
  D = 
       u1  u2  u3
   y1   0   0   0
   y2   0   0   0
   y3   0   0   0
 
Input groups:           
      Name      Channels
    ActualIn       3    
                        
Output groups:           
      Name       Channels
    ActualOut       3    
                         
Continuous-time state-space model.

Можно вычислить норму на выборках разницы между исходной неопределенной матрицей и результатом, образованным объединением Msys и Delta.

norm(usample(sys-lft(Delta,Msys),'p1',4,'p2',3),'inf') 
ans = 4×3

     0     0     0
     0     0     0
     0     0     0
     0     0     0
Открыть сценарий в реальном времени

Создание неопределенной матрицы A и получить неопределенную матрицу B использование неявного преобразования, imp2exp. Обратите внимание, что B имеет 2 неопределенных параметра R и K. Можно разложить B в определенную часть, Mи нормализованная неопределенная часть, Delta.

R = ureal('R',1,'Percentage',[-10 40]); 
K = ureal('K',2e-3,'Percentage',[-30 30]); 
A = [1 -R 0 -K;0 -K 1 0]; 
Yidx = [1 3]; 
Uidx = [4 2]; 
B = imp2exp(A,Yidx,Uidx); 
[M,Delta] = lftdata(B);

Та же самая операция может быть выполнена путем определения неопределенных параметров, K и R, подлежит извлечению.

[MK,DeltaR] = lftdata(B,'R'); 
MK 
MK =

  Uncertain matrix with 3 rows and 3 columns.
  The uncertainty consists of the following blocks:
    K: Uncertain real, nominal = 0.002, variability = [-30,30]%, 2 occurrences

Type "MK.NominalValue" to see the nominal value, "get(MK)" to see all properties, and "MK.Uncertainty" to interact with the uncertain elements.

[MR,DeltaK] = lftdata(B,'K'); 
MR 
MR =

  Uncertain matrix with 4 rows and 4 columns.
  The uncertainty consists of the following blocks:
    R: Uncertain real, nominal = 1, variability = [-10,40]%, 1 occurrences

Type "MR.NominalValue" to see the nominal value, "get(MR)" to see all properties, and "MR.Uncertainty" to interact with the uncertain elements.

simplify(B-lft(Delta,M)) 
ans = 2×2

     0     0
     0     0


simplify(B-lft(DeltaR,MK)) 
ans = 2×2

     0     0
     0     0


simplify(B-lft(DeltaK,MR)) 
ans = 2×2

     0     0
     0     0

Проверьте результат, полученный путем объединения двух результатов разложения.

[Mall,Deltaall] = lftdata(B,{'K';'R'}); 
Mall-M
ans = 5×5

     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0

См. также

|

Темы

Представлен до R2006a

Документация по инструментам надежного управления

Поддержка