Модели систем дискретного времени

Модели дискретно-временных систем являются представительными схемами для цифровых фильтров. Техническая вычислительная среда MATLAB ® поддерживает несколько моделей систем дискретного времени, которые описаны в следующих разделах:

Передаточная функция

Передаточная функция является базовым Z-доменным представлением цифрового фильтра, выражающим фильтр как отношение двух многочленов. Это основная дискретная модель для этой панели инструментов. Описание модели передаточной функции для Z-преобразования дифференциального уравнения цифрового фильтра

$Y (z) \frac{= b (1) +^{b} (2) z − 1^{+}}{. . . + b (n^{+} 1) z - {na}^{(}} 1) +$ a (2) z − 1 +... + a (m + 1) z − mX (z).

Здесь константы b (i) и a (i) являются коэффициентами фильтра, а порядок фильтра - максимум n и m. В среде MATLAB эти коэффициенты сохраняются в двух векторах (векторы строк по условию), один вектор строк для числителя и один для знаменателя. Для получения дополнительной информации о форме функции переноса см. Фильтры и функции переноса.

Нулевой коэффициент усиления

Факторизованная или нулевая форма усиления передаточной функции

$H (z) \frac{= q}{(z)} p \frac{(z) = k (z - q (1)) (z - q}{(2)) . . . (z - q (n)) (z - p}$ (1)) (z − p (2))... (z − p (n)).

По условию коэффициенты многочлена хранятся в векторах строк и корни многочлена в векторах столбцов. Таким образом, в форме «нулевой полюс-коэффициент усиления» нулевое и полюсное положения числителя и знаменателя передаточной функции находятся в векторах столбцов. Коэффициент усиления k факторизованной передаточной функции является скаляром MATLAB.

poly и roots функции преобразуют представления полиномов и нулевых полюсов. Например, простой фильтр IIR

b = [2 3 4];
a = [1 3 3 1];

Нули и полюса этого фильтра равны

q = roots(b)
p = roots(a)
% Gain factor
k = b(1)/a(1)

Возвращаясь к исходным многочленам,

bb = k*poly(q)
aa = poly(p)

Обратите внимание, что b и a в этом случае представляют собой передаточную функцию:

$H (z) \frac{= 2^{+} {3z}^{−}}{1 +^{} 4z -^{} 21^{+}} \frac{3z - 1^{} + 3z -}{^{2} +^{z} − 3} =$ z (2z2 + 3z + 4) z3 + 3z2 + 3z + 1.

Для b = [2 3 4], roots функция пропускает ноль для z, равного 0. Фактически, функция пропускает полюса и нули для z, равные 0, всякий раз, когда входная передаточная функция имеет больше полюсов, чем нули, или наоборот. Это приемлемо в большинстве случаев. Однако, чтобы обойти проблему, просто добавьте нули, чтобы сделать векторы одинаковой длины перед использованием roots функция; например, b = [b 0].

Пространство состояния

Всегда можно представить цифровой фильтр или систему дифференциальных уравнений как набор дифференциальных уравнений первого порядка. В матричной форме или форме state-space можно записать уравнения как

$\begin{matrix} x (n + 1) = Ax (n) \\ + Bu (n) y (n) = Cx (n) + Du (n \end{matrix}$ ),

где u - вход, x - вектор состояния, и y - выходной сигнал. Для одноканальных систем A является mоколо-m матрица, где m - порядок фильтра, B - вектор столбца, C является вектором строки, и D является скаляром. Нотация состояния-пространства особенно удобна для многоканальных систем, где вход u и выходные данные y стать векторами, и B, C, и D стать матрицами.

Представление пространства состояний легко распространяется на среду MATLAB. A, B, C, и D представляют собой прямоугольные массивы; Функции MATLAB рассматривают их как отдельные переменные.

Взятие Z-преобразования уравнений state-space и их объединение показывает эквивалентность форм state-space и передаточной функции:

$Y (z) = H (z) U (z), где {H (z)}^{=} C ($ zI − A) − 1B + D

Не беспокойтесь, если вы не знакомы с представлением состояния-пространства линейных систем. Некоторые алгоритмы конструкции фильтра используют форму state-space внутри, но не требуют каких-либо знаний концепций state-space для их успешного использования. Однако, если приложения широко используют обработку сигналов в пространстве состояний, обратитесь к продукту Control System Toolbox™ для получения полной библиотеки инструментов в пространстве состояний.

Частичное расширение фракции (форма остатка)

Каждая передаточная функция также имеет соответствующее частичное дробное расширение или представление формы остатка, данное

$\frac{b (z}{) a} (\frac{z) =}{r (1)^{1}} - p (\frac{1) z}{- 1 + .^{. .}} + r (n) 1^{-} p (n) z - 1 +^{k (1)}$ + k (2) z − 1 +... + k (m − n + 1) z − (m − n)

при условии, что H (z) не имеет повторяющихся полюсов. Здесь n - степень многочлена знаменателя рациональной передаточной функции b (z )/a (z). Если r - полюс _{кратности} sr, то H (z) имеет члены вида:

$\frac{r (j}{) 1 - p^{(}} j \frac{) z −}{{1 + r (j^{+}}^{1}}) (1 \frac{- p_{(} j)}{{z - 1) 2^{. .} .}^{_{+}}}$ r (j + sr − 1) (1 − p (j) z − 1) sr

Обработка сигналов Toolbox™ residuez функция в преобразует передаточные функции в форму расширения частичной дроби и из нее. “z"в конце residuez обозначает z-домен, или дискретный домен. residuez возвращает полюса в векторе столбца p, остатки, соответствующие полюсам в векторе-столбце rи любая неправильная часть исходной передаточной функции в векторе строки k. residuez определяет, что два полюса одинаковы, если величина их разности меньше 0,1 процента от любой из величин полюсов.

Частичное дробное расширение возникает при обработке сигнала как один из способов нахождения обратного Z-преобразования передаточной функции. Например, частичное дробное расширение

$H (z) \frac{= −^{4}}{+ {8z}^{−} 11^{+}}$ 6z − 1 + 8z − 2

является

b = [-4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)

который соответствует

$H (z) \frac{=}{−^{121}} + \frac{}{4z -^{1}}$ + 81 + 2z − 1

Чтобы найти обратное Z-преобразование H (z), найдите сумму обратных Z-преобразований двух аддендов H (z), давая причинно-импульсную характеристику:

$h (n) = {- 12}^{} (− {4)}^{n} + 8 (− 2)$ n, n = 0,1,2,...

Для проверки в среде MATLAB введите

imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
respres = filter(r(1),[1 -p(1)],imp)+...
  filter(r(2),[1 -p(2)],imp)

Секции второго порядка (SOS)

Любая передаточная функция H (z) имеет представление сечений второго порядка

$H (z)_{}^{}_{} =∏k=1LHk (z_{)}^{} \frac{_{}_{}^{}_{}^{}}{_{}_{}^{}_{}^{}}$ =∏k=1Lb0k+b1kz−1+b2kz−2a0k+a1kz−1+a2kz−2

где L - количество секций второго порядка, описывающих систему. Среда MATLAB представляет форму секции второго порядка дискретно-временной системы в виде массива L-by-6 sos. Каждая строка sos содержит одну секцию второго порядка, где элементы строки являются тремя числительными и тремя знаменательными коэффициентами, описывающими секцию второго порядка.

$SOS = \begin{array}{l} _{} & _{} & _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} & _{} & _{} \\ _{} & _{} & _{} & _{} & _{} & _{} \end{array} (b01b11b21a01a11a21b02b12b22a02a12a22 b0Lb1Lb2La0La1La2L$ )

Существует множество способов представления фильтра в форме раздела второго порядка. Благодаря тщательному спариванию пар полюсов и нулей, упорядочению секций в каскаде и мультипликативному масштабированию секций можно уменьшить усиление шума квантования и избежать переполнения в некоторых реализациях фильтра с фиксированной точкой. Функции zp2sos и ss2sos, описанные в разделе Линейные системные преобразования (Linear System Transformations), выполняют спаривание полюсов и нулей, масштабирование сечений и упорядочение сечений.

Примечание

Все преобразования второго порядка панели инструментов обработки сигналов применяются только к цифровым фильтрам.

Структура решетки

Для дискретного всеполюсного или нулевого фильтра N-го порядка, описанного полиномиальными коэффициентами a (n), n = 1 , 2 ,..., N + 1, существует N соответствующих коэффициентов структуры решетки k (n) , n = 1, 2,.. ., N. Параметры k (n) также называются коэффициентами отражения фильтра. Учитывая эти коэффициенты отражения, можно реализовать дискретный фильтр, как показано ниже.

Схемы структуры решётчатого фильтра FIR и IIR

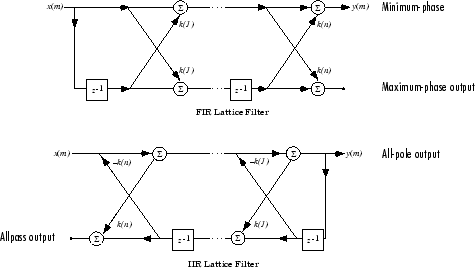
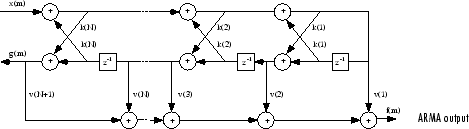
Для общего полюсно-нулевого БИХ-фильтра, описанного полиномиальными коэффициентами a и b, существуют как коэффициенты решетки k (n) для знаменателя a, так и коэффициенты лестницы v (n) для числителя b. Решетчатый/лестничный фильтр может быть реализован как

Схема решетчатого/лестничного фильтра

Функция панели инструментов tf2latc принимает фильтр FIR или IIR в полиномиальной форме и возвращает соответствующие коэффициенты отражения. Примером фильтра FIR в полиномиальной форме является

b = [1.0000   0.6149   0.9899   0.0000   0.0031  -0.0082];

Это представление решетки фильтра (коэффициент отражения)

k = tf2latc(b)

Для БИХ-фильтров величина коэффициентов отражения обеспечивает легкую проверку стабильности. Если все коэффициенты отражения, соответствующие многочлену, имеют величину меньше 1, все корни этого многочлена находятся внутри единичной окружности. Например, рассмотрим БИХ-фильтр с числительным полиномом b сверху и многочлен знаменателя:

a = [1 1/2 1/3];

Представление решетки фильтра:

[k,v] = tf2latc(b,a);

Поскольку abs(k) < 1 для всех коэффициентов отражения в k, фильтр стабилен.

Функция latc2tf вычисляет полиномиальные коэффициенты для фильтра по его коэффициентам решетки (отражения). Учитывая вектор коэффициента отражения k, соответствующая полиномиальная форма

b = latc2tf(k);

Коэффициенты решётки или решётки/лестницы могут использоваться для реализации фильтра с использованием функции latcfilt.

Матрица свертки

При обработке сигнала свертывание двух векторов или матриц эквивалентно фильтрации одного из входных операндов другим. Это соотношение позволяет представить цифровой фильтр в виде матрицы свертки.

При любом векторе функция панели инструментов convmtx генерирует матрицу, внутреннее произведение которой с другим вектором эквивалентно свертке двух векторов. Сгенерированная матрица представляет собой цифровой фильтр, который можно применить к любому вектору соответствующей длины; внутренний размер операндов должен быть согласован для вычисления внутреннего продукта.

Матрица свертки для вектора b, представляющий числительные коэффициенты для цифрового фильтра,

b = [1 2 3];
x = randn(3,1);
C = convmtx(b',3);

Два эквивалентных способа свертки b с x являются следующими.

y1 = C*x;
y2 = conv(b,x);

Документация