Блэкман, плоский верх, окна Хэмминга, Ханна и прямоугольные - все это особые случаи обобщённого косинусного окна. Эти окна представляют собой комбинации синусоидальных последовательностей с частотами, кратными 2δ/( N - 1), где N - длина окна. Один частный случай - окно Блэкмана:
N = 128; A = 0.42; B = 0.5; C = 0.08; ind = (0:N-1)'*2*pi/(N-1); w = A - B*cos(ind) + C*cos(2*ind);
Изменение значений констант A, B, и C в предыдущем выражении генерирует различные обобщенные окна косинусов, такие как окна Хэмминга и Ханна. Добавление дополнительных косинусных членов более высокой частоты создает плоское верхнее окно. Концепция, лежащая в основе этих окон, заключается в том, что, суммируя отдельные члены для формирования окна, низкочастотные пики в частотной области объединяются таким образом, чтобы уменьшить высоту боковой зоны. Это имеет побочный эффект увеличения ширины основного блока.
Окна Хэмминга и Ханна являются двухсрочными обобщёнными окнами косинусов, заданными A = 0.54, B = 0.46 для Хэмминга и A = 0.5, B = 0.5 для Ханна.
Обратите внимание, что определение обобщенного косинусного окна, показанное в предыдущем коде MATLAB ®, дает нули в выборках 1 иn для A = 0.5 и B = 0.5.
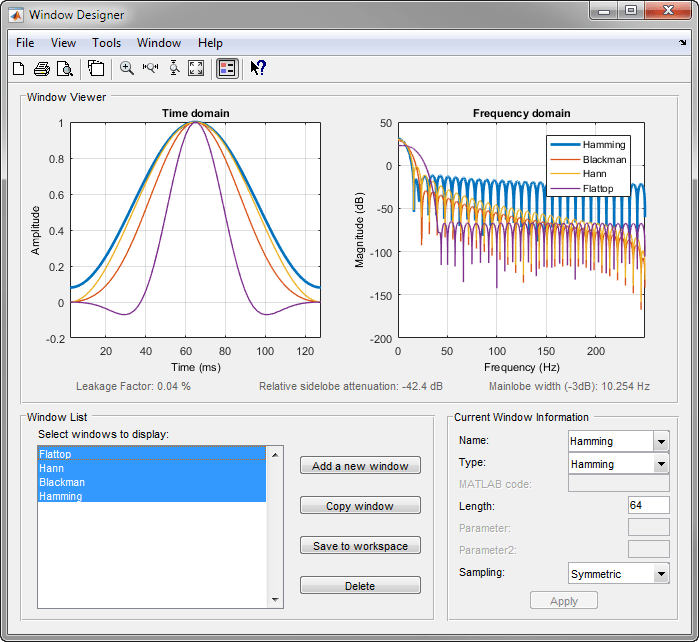
Этот снимок экрана Windows Designer сравнивает окна Blackman, Hamming, Hann и Flat Top.
blackman | flattopwin | hamming | hann | WVTool