Вы часто можете сформулировать математическую систему, которую вы моделируете, несколькими способами. Выбор наилучшей математической модели позволяет выполнять моделирование быстрее и точнее. Например, рассмотрим простую последовательную схему RLC.
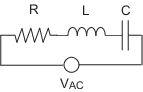
Согласно закону Кирхоффа о напряжении, падение напряжения на этой цепи равно сумме падения напряжения на каждом элементе цепи.
VL + VC
Используя закон Ома для решения напряжения на каждом элементе цепи, уравнение для этой цепи можно записать как
dt
Вы можете смоделировать эту систему в Simulink ®, решив либо напряжение резистора, либо напряжение индуктора. Выбор решения для влияет на структуру модели и ее производительность.
Решение RLC-схемы для напряжения резистора дает
dt
На следующей диаграмме показано это уравнение, смоделированное в Simulink, где R является 70, C - 0.00003, и L является 0.04. Напряжение резистора представляет собой сумму напряжения источника, напряжения конденсатора и напряжения индуктора. Ток в цепи необходим для вычисления напряжений конденсатора и индуктора. Чтобы вычислить ток, умножьте напряжение резистора на коэффициент усиления 1/R. Вычислите напряжение конденсатора путем интегрирования тока и умножения на коэффициент усиления 1/C. Вычислите напряжение индуктора, взяв производную тока и умножив на коэффициент усиления L.
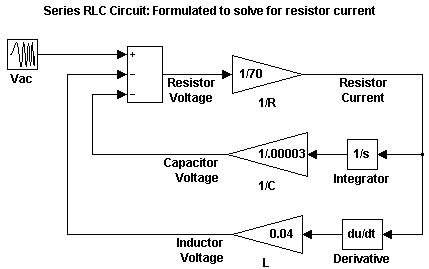
Эта композиция содержит производный блок, связанный с индуктором. По возможности следует избегать математических формулировок, которые требуют производных блоков, поскольку они вводят разрывы в системе. Численная интеграция используется для решения динамики модели во времени. Эти интеграционные решатели предпринимают небольшие шаги во времени, чтобы удовлетворить ограничение точности решения. Если разрыв, введенный блоком Производная, слишком велик, решатель не сможет перейти через него.
Кроме того, в этой модели блоки Производная, Сумма и два Усиления создают алгебраический цикл. Алгебраические циклы замедляют выполнение модели и могут давать менее точные результаты моделирования. Дополнительные сведения см. в разделе Концепции алгебраического цикла.
Чтобы избежать использования блока Производная, сформулируйте уравнение для определения напряжения индуктора.
dt
На следующей диаграмме показано это уравнение, смоделированное в Simulink. Напряжение индуктора представляет собой сумму напряжения источника, напряжения резистора и напряжения конденсатора. Ток в цепи необходим для вычисления напряжений резистора и конденсатора. Чтобы вычислить ток, интегрируйте напряжение индуктора и делите на L. Рассчитайте напряжение конденсатора путем интегрирования тока и деления на C. Рассчитайте напряжение резистора путем умножения тока на коэффициент усиления R.
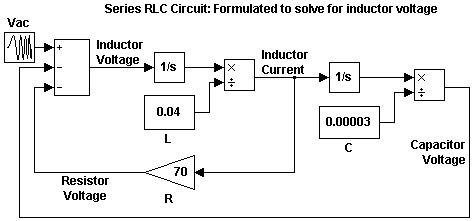
Эта модель содержит только блоки интеграторов и не содержит алгебраических циклов. В результате модель моделируется быстрее и точнее.