Робертсон [1] создал систему автокаталитических химических реакций для тестирования и сравнения числовых решателей для жестких систем. Реакции, константы скорости (k) и скорости реакции (V) для системы даны следующим образом:
С]
Поскольку существуют большие различия между скоростями реакции, числовые решатели считают дифференциальные уравнения жесткими. Для жестких дифференциальных уравнений некоторые числовые решатели не могут сходиться в решении, если размер шага не является чрезвычайно малым. Если размер шага чрезвычайно мал, время моделирования может быть недопустимо большим. В этом случае необходимо использовать числовой решатель, предназначенный для решения жестких уравнений.
Система обыкновенных дифференциальных уравнений (ОДУ) имеет следующие характеристики:
Все уравнения являются обычными дифференциальными уравнениями.
Каждое уравнение является производной зависимой переменной относительно одной независимой переменной, обычно времени.
Количество уравнений равно количеству зависимых переменных в системе.
Используя скорости реакции, можно создать набор дифференциальных уравнений, описывающих скорость изменения для каждого химического вида. Поскольку существует три вида, в математической модели существует три дифференциальных уравнения.
Исходные условия: 1= 0 C = 0.
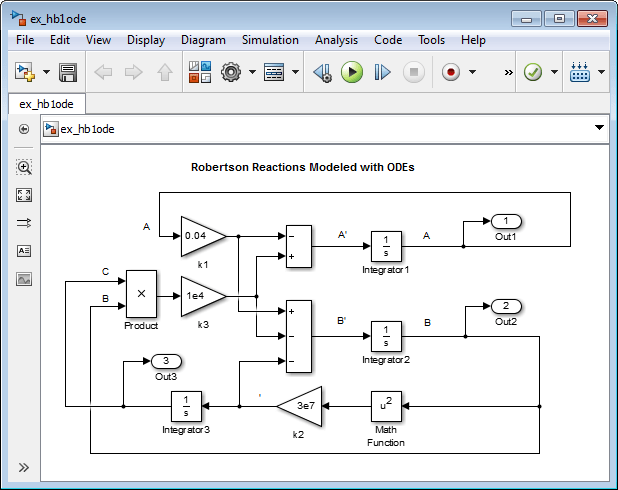
Создание модели или открытие модели ex_hb1ode.
Добавьте в модель три блока Integrator. Маркировка входов A', B', и C'и выходные данные A, B, и C соответственно.
Добавьте блоки Sum, Product и Gain для решения каждой дифференциальной переменной. Например, для моделирования сигнала C',
Добавление блока математической функции и подключение входа к сигналу B. Задайте для параметра Function значение square.
Подключите выход блока математической функции к блоку усиления. Задайте для параметра Gain значение 3e7.
Продолжайте добавлять оставшиеся члены дифференциального уравнения в модель.
Смоделировать исходное состояние A путем установки параметра Initial condition для A Блок интегратора для 1.
Добавление блоков для сохранения сигналов A, B, и C к переменной MATLAB yout.
Создание сценария, использующего sim для моделирования модели. Этот сценарий сохраняет результаты моделирования в переменной MATLAB yout. Поскольку моделирование имеет большой интервал времени и B первоначально изменяется очень быстро, печать значений по логарифмической шкале помогает визуально сравнивать результаты. Также, поскольку значение B мал относительно значений A и C, умножить B путем перед выводом значений на печать.
Введите следующие операторы в сценарий MATLAB ®. При создании собственной модели заменитеex_hblode с именем модели.
sim('ex_hb1ode')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with ODEs')В редакторе Simulink ® на вкладке Моделирование (Modeling) щелкните Параметры модели (Model Settings ).
- на панели «Решатель» установите для параметра «Время остановки» значение 4e5 и решатель для ode15s (stiff/NDF).
- На панели Импорт данных установите флажки Время и Вывод.
Запустите сценарий. Обратите внимание, что все A преобразуется в C.
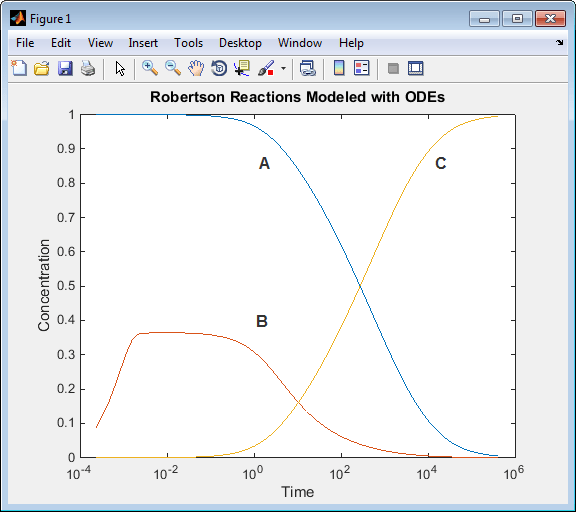
Система дифференциальных алгебраических уравнений (DAE) имеет следующие характеристики:
Он содержит как обычные дифференциальные уравнения, так и алгебраические уравнения. Алгебраические уравнения не имеют никаких производных.
Только некоторые из уравнений являются дифференциальными уравнениями, определяющими производные некоторых зависимых переменных. Другие зависимые переменные определяются алгебраическими уравнениями.
Количество уравнений равно количеству зависимых переменных в системе.
Некоторые системы содержат ограничения из-за законов о сохранении, такие как сохранение массы и энергии. Если установить начальные концентрации 1= 0 C = 0, общая концентрация трех видов всегда равна 1, + B + C = 1. Можно заменить дифференциальное уравнение для C′with следующего алгебраического уравнения, чтобы создать набор дифференциальных алгебраических уравнений (DAE).
A − B
Дифференциальные переменные A и B однозначно определить алгебраическую переменную C.
Исходные условия: = 0.
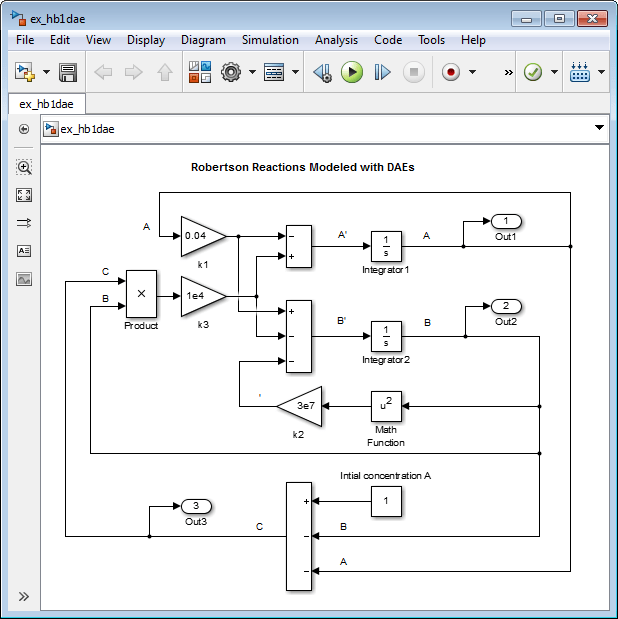
Внесение этих изменений в модель или модель ex_hb1odeили откройте модель ex_hb1dae.
Удаление блока интегратора для вычисления C.
Добавьте блок Sum и установите для параметра List of signes значение + - -.
Подключите сигналы A и B к минусовым входам блока Sum.
Смоделировать начальную концентрацию A с блоком Константа, подключенным к плюсовому входу блока Сумма. Задайте для параметра Constant value значение 1.
Подключите выход блока Sum к разветвленной линии, соединенной с блоками Product и Out.
Создание сценария, использующего sim для моделирования модели.
Введите следующие операторы в сценарий MATLAB. При создании собственной модели замените ex_hbldae с именем модели.
sim('ex_hb1dae')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with DAEs')В редакторе Simulink на вкладке Моделирование (Modeling) щелкните Параметры модели (Model Settings).
- на панели «Решатель» установите для параметра «Время остановки» значение 4e5 и решатель для ode15s (stiff/NDF).
- На панели Импорт данных установите флажки Время и Вывод.
Запустите сценарий. Результаты моделирования при использовании алгебраического уравнения аналогичны результатам моделирования модели с использованием только дифференциальных уравнений.
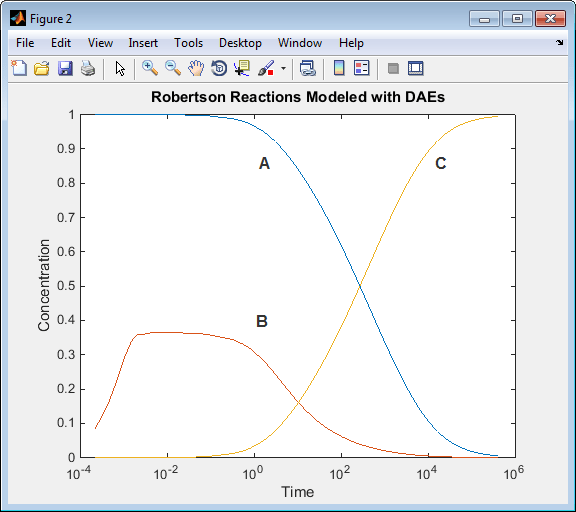
Некоторые системы содержат ограничения из-за законов о сохранении, такие как сохранение массы и энергии. Если установить начальные концентрации 1= 0 C = 0, общая концентрация трех видов всегда равна 1, + B + C = 1.
Можно заменить дифференциальное уравнение для C′with алгебраического уравнения, смоделированного с помощью блока алгебраического ограничения и блока суммы. Блок алгебраического ограничения ограничивает свой входной сигнал F (z) нулем и выводит алгебраическое состояние z. Другими словами, блочный выход является значением, необходимым для получения нуля на входе. Для ввода в блок используйте следующее алгебраическое уравнение.
+ C − 1
Дифференциальные переменные A и B однозначно определить алгебраическую переменную C.
Исходные условия: 1= 0 C=1⋅10−3.
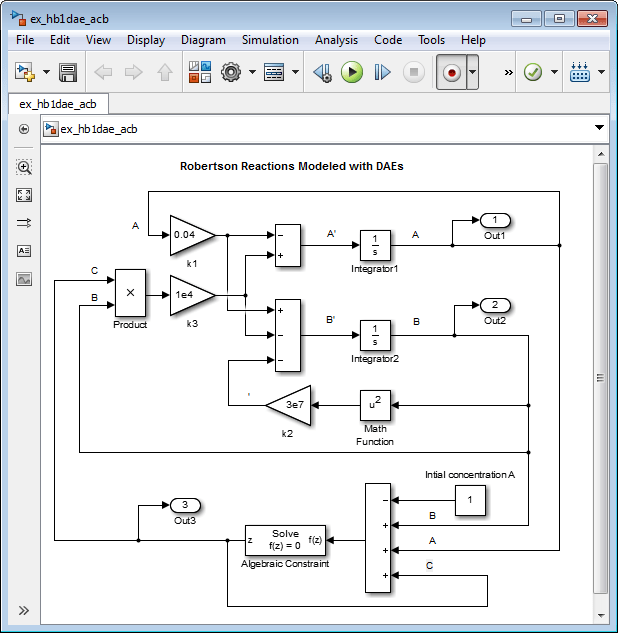
Внесение этих изменений в модель или модель ex_hb1odeили откройте модель ex_hb1dae_acb.
Удаление блока интегратора для вычисления C.
Добавьте блок «Алгебраическая зависимость». Задайте для параметра Начальное приближение значение 1e-3.
Добавьте блок «Сумма». Установите для параметра List of signes значение - + + +.
Подключите сигналы A и B к плюс входам блока Sum.
Смоделировать начальную концентрацию A с блоком Константа, подключенным к минусовому входу блока Сумма. Задайте для параметра Constant value значение 1.
Подключите выход блока алгебраических ограничений к разветвленной линии, подключенной к входам блоков «Изделие» и «Выход».
Создайте линию ответвления от выхода блока Алгебраической зависимости к окончательному плюс-входу блока Сумма.
Создание сценария, использующего sim для моделирования модели.
Введите следующие операторы в сценарий MATLAB. При создании собственной модели замените ex_hbl_acb с именем модели.
sim('ex_hb1dae_acb')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with DAEs and Algebraic Constraint Block')В редакторе Simulink на вкладке Моделирование (Modeling) щелкните Параметры модели (Model Settings).
- на панели «Решатель» установите для параметра «Время остановки» значение 4e5 и решатель для ode15s (stiff/NDF).
- На панели Импорт данных установите флажки Время и Вывод.
Запустите сценарий. Результаты моделирования при использовании блока алгебраической зависимости совпадают с результатами моделирования модели с использованием только дифференциальных уравнений.
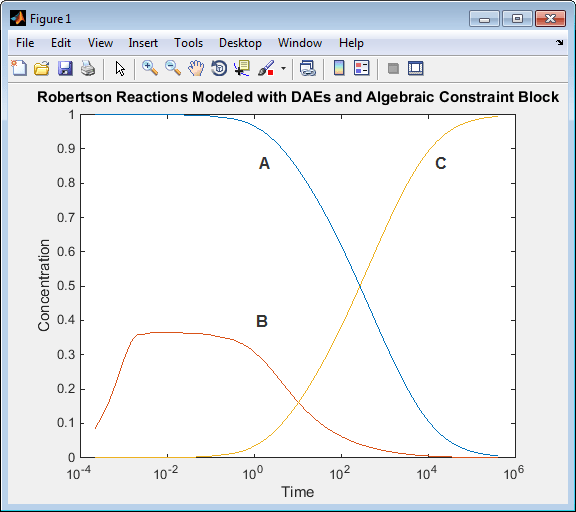
Использование блока алгебраического ограничения создает алгебраический цикл в модели. Если для параметра алгебраического цикла задано значение warning (на вкладке Моделирование (Modeling) щелкните Настройки модели (Model Settings), а затем выберите Диагностика (Diagnostics)), во время моделирования в средстве просмотра диагностики отображается следующее сообщение.
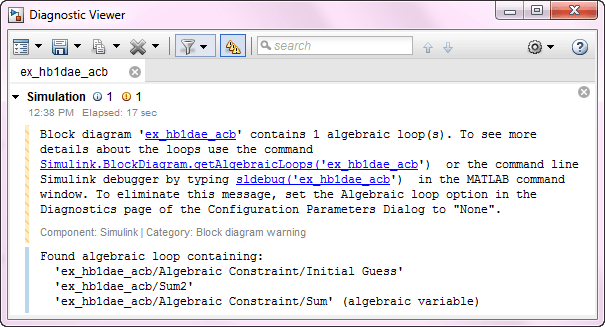
Для этой модели решатель алгебраических циклов смог найти решение для моделирования, но алгебраические циклы не всегда имеют решение, и они не поддерживаются для генерации кода. Дополнительные сведения о алгебраических контурах в моделях Simulink и их удалении см. в разделе Концепции алгебраических контуров.
[1] Робертсон, H. H. «Решение ряда уравнений темпа реакции». Численный анализ: введение (J. Walsh ed.). Лондон, Англия: Academic Press, 1966, стр. 178-182.