В модели Simulink ® алгебраический цикл возникает, когда существует сигнальный цикл с только блоками прямого прохождения внутри цикла. Прямой проход означает, что Simulink необходимо значение входного сигнала блока для вычисления его выходного сигнала на текущем временном шаге. Такой сигнальный контур создает круговую зависимость выходных и входных сигналов блока за один и тот же временной шаг. Это приводит к алгебраическому уравнению, которое необходимо решать на каждом временном шаге, добавляя вычислительные затраты к моделированию .
Некоторые примеры блоков с прямыми входами:
State-Space, если коэффициент матрицы D не равен нулю
Перенос Fcn, если числитель и знаменатель имеют одинаковый порядок
Нулевой полюс, когда блок имеет столько нулей, сколько полюсов
Непрямые блоки сквозного канала поддерживают переменную State. Два примера - интегратор и единичная задержка.
Совет
Чтобы определить, имеет ли блок прямой проход, ознакомьтесь с разделом «Характеристики» страницы ссылок на блок.
На рисунке показан пример алгебраического цикла. Блок Суммы является алгебраической переменной xa, которая ограничена равным первому входу u минус xa (например, xa = u - xa).
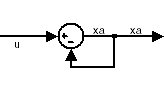
Решением этого простого цикла является xa = u/2.
Simulink содержит набор числовых решателей для моделирования обыкновенных дифференциальных уравнений (ОДУ), которые представляют собой системы уравнений, которые можно записать как
),
где x - вектор состояния, а t - независимая переменная времени.
Некоторые системы уравнений содержат дополнительные ограничения, которые включают независимую переменную и вектор состояния, но не производную вектора состояния. Такие системы называются дифференциальными алгебраическими уравнениями (DAE),
Термин алгебраический относится к уравнениям, которые не включают никаких производных. Дисковые полки, возникающие при проектировании, можно выразить в полуявном виде
, xa, t),
где:
f и g могут быть векторными функциями.
Первое уравнение - это дифференциальное уравнение.
Второе уравнение - алгебраическое уравнение.
Вектор дифференциальных переменных равен x.
Вектор алгебраических переменных - xa.
В моделях Simulink алгебраические петли являются алгебраическими ограничениями. Модели с алгебраическими петлями определяют систему дифференциальных алгебраических уравнений. Simulink решает алгебраические уравнения (алгебраический цикл) численно для xa на каждом шаге решателя ОДУ.
Модель на рисунке эквивалентна этой системе уравнений в полуявном виде:
= − x + u − 2xa.
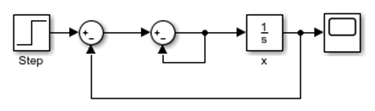
На каждом шаге решателя ОДУ решатель алгебраического цикла должен решить алгебраическое ограничение для xa перед вычислением производной.
Алгебраические ограничения:
Происходят при моделировании физических систем, часто из-за законов сохранения, таких как сохранение массы и энергии
Возникает при выборе определенной системы координат для модели
Помощь в наложении ограничений проектирования на отклики системы в динамической системе
Используйте Simscape™ для моделирования систем, которые охватывают механические, электрические, гидравлические и другие физические области в качестве физических сетей. Simscape создает дисковые полки, характеризующие поведение модели. Программное обеспечение интегрирует эти уравнения с остальной частью модели, а затем непосредственно решает дисковые полки. Simulink решает переменные для компонентов в различных физических областях одновременно, избегая проблем с алгебраическими циклами.
Искусственный алгебраический цикл возникает, когда атомная подсистема или блок модели заставляет Simulink обнаруживать алгебраический цикл, даже если содержимое подсистемы не содержит прямого прохождения от входа к выходу. При создании атомной подсистемы все блоки Inport проходят прямой канал, что приводит к образованию алгебраического цикла.
Начните с включенной модели, которая представляет простой пропорциональный контроль установки, описанной

которые могут быть переписаны в форме state-space как
![$$
\dot{x} = \left[
 \begin{array}{cc}
 -2 & -1 \\
1 & 0
 \end{array}
 \right]
+ \left(
\begin{array}{c}
0\\1
\end{array}
\right)
$$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq09529265284802621175.png)
![$$
y = \left[\begin{array}{cc}0&1\end{array}\right]
$$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq01044250964337862021.png)
Система не имеет ни алгебраических переменных, ни прямого прохождения и не содержит алгебраического цикла.

Измените модель, как описано в следующих шагах.
Заключите блоки контроллера и установки в подсистему.
В диалоговом окне подсистемы выберите Обработать как атомную единицу, чтобы сделать подсистему атомной.
На панели Диагностика (Diagnostics) окна Параметры конфигурации модели (Model Configuration Parameters) задайте для параметра Алгебраический цикл (Algebraic Loop) значение error.

При моделировании этой модели возникает алгебраический цикл, поскольку подсистема является прямой, даже если путь в атомной подсистеме не является прямым. Моделирование останавливается с алгебраической ошибкой цикла.
Когда модель содержит алгебраический цикл, Simulink использует нелинейный решатель на каждом шаге времени для решения алгебраического цикла. Решатель выполняет итерации для определения решения алгебраического ограничения, если таковое имеется. В результате модели с алгебраическими петлями могут работать медленнее, чем модели без алгебраических петель.
Simulink использует алгоритм области доверия dogleg для решения алгебраических циклов. Используемый допуск меньше, чем решатель ODE Reltol и Abstol. Это происходит потому, что Симулинк использует «явный метод ОДУ» для решения Index-1 дифференциальных алгебраических уравнений (DAE).
Для работы алгебраического решателя цикла:
Должен быть один блок, где решатель цикла может разорвать цикл и попытаться решить его.
Модель должна иметь реальные двойные сигналы.
Основное алгебраическое ограничение должно быть гладкой функцией
Например, предположим, что модель имеет блок суммы с двумя входами - один аддитивный, другой вычитаемый. При подаче выходных данных блока суммы на один из входов создается алгебраический цикл, в котором все блоки включают прямой проход.

Блок Sum не может вычислить выходной сигнал, не зная входного сигнала. Simulink обнаруживает алгебраический цикл, а решатель алгебраического цикла решает цикл с помощью итеративного цикла. В примере блока Sum программное обеспечение вычисляет правильный результат следующим образом:
| xa (t) = u (t )/2. | (1) |
Решатель алгебраического цикла использует метод поиска на основе градиента, который требует непрерывных первых производных алгебраического ограничения, которые соответствуют алгебраическому циклу. В результате, если алгебраический цикл содержит разрывы, решатель алгебраического цикла может выйти из строя.
Для получения дополнительной информации см. раздел Решение Index-1 дисковых полок в MATLAB и Simulink []1
Решатель алгебраических циклов Simulink использует один из двух алгоритмов для решения алгебраических циклов:
Доверительный регион
Поиск по строке
По умолчанию Simulink выбирает наилучший алгебраический решатель цикла и может переключаться между двумя методами во время моделирования. Чтобы явно включить автоматический выбор решателя алгебраических циклов для модели, в командной строке MATLAB ® введите:
set_param(model_name, 'AlgebraicLoopSolver','Auto');
Для переключения на алгоритм доверительной области в командной строке MATLAB введите:
set_param(model_name, 'AlgebraicLoopSolver', 'TrustRegion');
Если решатель алгебраического цикла не может решить алгебраический цикл с помощью алгоритма доверительной области, попробуйте смоделировать модель с помощью алгоритма поиска линий.
Для перехода к алгоритму поиска строк в командной строке MATLAB введите:
set_param(model_name, 'AlgebraicLoopSolver', 'LineSearch');
Дополнительные сведения см. в разделе:
Программа «Фортран» HYBRD1 в Руководство пользователя для MINPACK-1 [2]
«Подпрограмма Фортрана Пауэлла для решения систем в нелинейных уравнениях», в «Численных методах нелинейных алгебраических уравнений» [3 ]
Методы доверительной области для нелинейной минимизации (панель инструментов оптимизации).
Поиск строк (панель инструментов оптимизации).
Алгебраическое решение цикла - итеративный процесс. Решатель алгебраического цикла Симулинка успешен только в том случае, если алгебраический цикл сходится к определённому ответу. Когда цикл не сходится или сходится слишком медленно, моделирование завершается с ошибкой.
Решатель алгебраических циклов не может решить алгебраические циклы, которые содержат любое из следующего:
Блоки с дискретными выходами
Блоки с неразъемными или сложными выходами
Неоднородности
Диаграммы Stateflow ®
Если модель содержит алгебраический цикл:
Невозможно создать код для модели.
Решатель алгебраического цикла Simulink может оказаться не в состоянии решить алгебраический цикл.
В то время как Simulink пытается решить алгебраический цикл, моделирование может выполняться медленно.
Для большинства моделей алгебраический решатель цикла является вычислительно дорогим для первого шага времени. Simulink быстро решает последующие временные шаги, потому что хорошая начальная точка для xa доступна с предыдущего временного шага.
Алгебраическое ограничение | Сравнить решатели | Состояние дескриптора - пространство | Обнаружение пересечения нулей
[1] Шампин, Лоуренс Ф., М.В.Рейхельт и Я.А.Киерценка. «Решение Index-1 дисковых полок в MATLAB и Simulink». Сиам Review.Vol.18,No.3,1999,pp.538-552.
[2] Другие, J.J., B.S.Garbow и K.E.Hillstrom. Руководство пользователя для MINPACK-1. Аргонн, IL: Argonne National Laboratory,1980.
[3] Рабиновиц, Филипп, ред. Численные методы для нелинейных алгебраических уравнений, Нью-Йорк: Гордон и Break Science Publishers, 1970.