Решатели с переменными шагами изменяют размер шага во время моделирования, уменьшая размер шага для повышения точности при быстром изменении состояний модели и увеличивая размер шага, чтобы избежать ненужных шагов при медленном изменении состояний модели. Вычисление размера шага увеличивает вычислительные издержки на каждом шаге, но может уменьшить общее количество шагов и, следовательно, время моделирования, необходимое для поддержания заданного уровня точности для моделей с быстро меняющимися или кусочно непрерывными состояниями.
Если для элемента управления Тип (Type) панели конфигурации решателя задано значение Variable-step, элемент управления Решатель (Solver) позволяет выбрать один из решателей с переменным шагом. Как и в случае решателей с фиксированным шагом, набор решателей с переменным шагом содержит дискретный решатель и набор решателей с непрерывным управлением. Однако, в отличие от решателей с фиксированным шагом, размер шага динамически изменяется в зависимости от локальной ошибки.
Выбор между двумя типами решателей с переменным шагом зависит от того, определяют ли блоки в модели состояния и, если да, то тип состояний, которые они определяют. Если модель не определяет состояний или определяет только дискретные состояния, выберите дискретный решатель. Если модель имеет непрерывные состояния, непрерывные решатели используют численное интегрирование для вычисления значений непрерывных состояний на следующем шаге времени.
Примечание
Если модель не имеет состояний или только дискретных состояний, Simulink ® использует дискретный решатель для моделирования модели, даже если указан непрерывный решатель.
Используйте дискретный решатель с переменным шагом, если модель не содержит непрерывных состояний. Для таких моделей дискретный решатель с переменным шагом уменьшает размер шага, чтобы фиксировать события модели, такие как пересечение нуля, и увеличивает размер шага, когда возможно улучшить производительность моделирования.
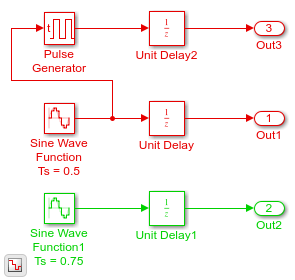
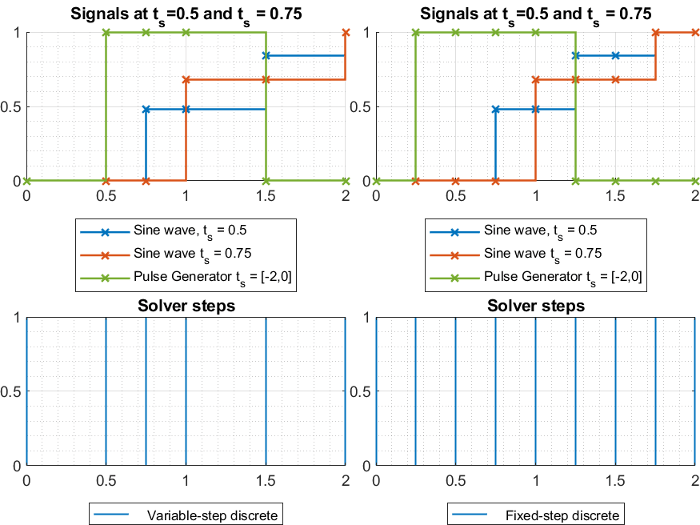
Модель, показанная на рисунке, содержит два дискретных синусоидальных сигнала при времени выборки 0,5 и 0,75. На графиках ниже показаны сигналы в модели вместе с шагами решателя для дискретных решателей с переменным шагом и дискретных решателей с фиксированным шагом соответственно. Можно видеть, что решатель переменных шагов выполняет только шаги, необходимые для записи выходного сигнала из каждого блока. С другой стороны, решатель с фиксированным шагом должен моделировать с фиксированным размером шага - или временем основной выборки - 0,25 для записи всех сигналов, таким образом делая больше шагов в целом.
Решатели переменных шагов динамически изменяют размер шага во время моделирования. Каждый из этих решателей увеличивает или уменьшает размер шага, используя локальное управление ошибками для достижения заданных допусков. Вычисление размера шага на каждом временном шаге увеличивает вычислительные издержки. Однако это может уменьшить общее количество шагов и время моделирования, необходимое для поддержания заданного уровня точности.
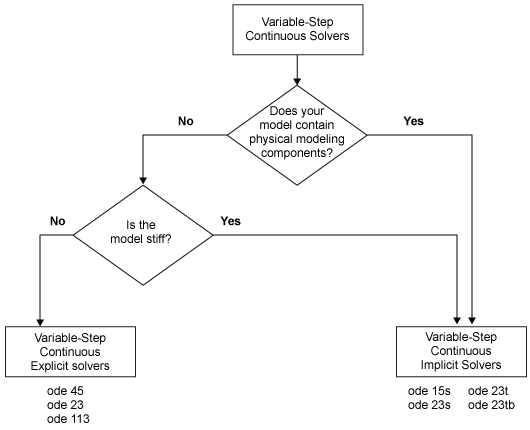
Можно далее классифицировать непрерывные решатели с переменными шагами как одношаговые или многошаговые, одношаговые или переменный порядок и явные или неявные. Дополнительные сведения см. в разделе Одношаговые и многошаговые решатели непрерывного действия.
Явные решатели с переменными шагами предназначены для решения проблем, не связанных с жесткостью. Simulink предоставляет четыре таких решателя:
ode45
ode23
ode113
odeN
| Решатель ОДУ | Одностадийный метод | Многоступенчатый метод | Порядок точности | Метод |
|---|---|---|---|---|
ode45 | X | Среда | Рунге-Кутта, Дорманд-Принс (4,5) пара | |
ode23 | X | Низко | Рунге-Кутта (2,3) пара Богацки и Шампина | |
ode113 | X | Переменная, от низкого до высокого | Осуществление Конвенции Адамса-Башфорта-Мултона | |
odeN | X | См. раздел Порядок точности в решателях с непрерывным непрерывным фиксированным шагом | См. раздел Методика интеграции в решателях с непрерывным непрерывным фиксированным шагом |
Примечание
Выберите odeN решатель, когда скорость моделирования важна, например, когда
Модель содержит множество пересечений нуля и/или сбросов решателя
Профилировщик решателя не обнаруживает неудачных шагов при профилировании модели
Если проблема жесткая, попробуйте использовать один из неявных решателей с переменным шагом:
ode15s
ode23s
ode23t
ode23tb
| Решатель ОДУ | Одностадийный метод | Многоступенчатый метод | Порядок точности | Метод сброса решателя | Макс. Заказ | Метод |
|---|---|---|---|---|---|---|
ode15s | X | Переменная, от низкой до средней | X | X | Формулы численного дифференцирования (NDF) | |
ode23s | X | Низко | Модифицированная формула Розенброка второго порядка | |||
ode23t | X | Низко | X | Трапециевидное правило с использованием интерполятора | ||
ode23tb | X | Низко | X | TR-BDF2 |
Для ode15s, ode23t, и ode23tb раскрывающееся меню для метода сброса решателя появляется в разделе Сведения о решателе (Solver details) на панели Конфигурация (Configuration). Этот параметр управляет тем, как решатель обрабатывает сброс, вызванный, например, обнаружением пересечения нуля. Разрешенные параметры: Fast и Robust. Fast указывает, что решатель не пересчитывает якобиан для сброса решателя, тогда как Robust указывает, что решатель это делает. Следовательно, Fast настройка выполняется вычислительно быстрее, но в некоторых случаях может использоваться небольшой размер шага. Для проверки таких случаев выполните моделирование с каждой настройкой и сравните результаты. Если в результатах нет разницы, можно безопасно использовать Fast настройка и экономия времени. Если результаты значительно отличаются, попробуйте уменьшить размер шага для быстрого моделирования.
Для ode15s решатель можно выбрать максимальный порядок применяемых формул числового дифференцирования (NDF). С момента ode15s использует формулы первого-пятого порядка, Maximum order позволяет выбирать заказы с 1 по 5. В случае острой проблемы может потребоваться начать с заказа 2.
В следующей таблице приведены советы по применению неявных решателей с переменным шагом. Пример сравнения поведения этих решателей см. в разделе Исследование решателей с переменным шагом с использованием жесткой модели.
Примечание
Для жесткой проблемы решения могут изменяться в масштабе времени, который очень мал по сравнению с интервалом интеграции, в то время как решение, представляющее интерес, изменяется в гораздо более длительном масштабе времени. Методы, которые не предназначены для жестких проблем, неэффективны в интервалах, где решение меняется медленно, потому что эти методы используют временные шаги, достаточно малые для разрешения наиболее быстрого возможного изменения. Для получения дополнительной информации см. Champine, L.F., Numerical Solution of Ordinary Differential Equations, Chapman & Hall, 1994.
Решатели с переменным шагом используют стандартные методы управления для контроля локальной ошибки на каждом временном шаге. В течение каждого временного шага решатели вычисляют значения состояния в конце шага и определяют локальную ошибку - оценочную ошибку этих значений состояния. Затем они сравнивают локальную ошибку с приемлемой ошибкой, которая является функцией как относительного допуска (rtol), так и абсолютного допуска (atol). Если локальная ошибка превышает допустимую для любого одного состояния, решатель уменьшает размер шага и повторяет попытку.
Относительный допуск измеряет ошибку относительно размера каждого состояния. Относительный допуск представляет процент от значения состояния. Значение по умолчанию 1e-3 означает, что вычисленное состояние является точным в пределах 0,1%.
Абсолютный допуск - пороговое значение ошибки. Этот допуск представляет приемлемую ошибку, так как значение измеренного состояния приближается к нулю.
Решатели требуют ошибки для iВ-й штат, ei, удовлетворить:
атоли).
На следующем рисунке показан график состояния и областей, в которых относительный допуск и абсолютный допуск определяют приемлемую ошибку.
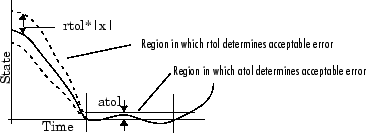
Модель имеет глобальный абсолютный допуск, который можно задать на панели Решатель (Solver) диалогового окна Параметры конфигурации (Configuration Parameters). Этот допуск применяется ко всем состояниям в модели. Можно указать auto или реальный скаляр. При указании auto (по умолчанию), Simulink первоначально устанавливает абсолютный допуск для каждого состояния на основе относительного допуска. Если относительный допуск больше 1e-3, abstol инициализируется в 1e-6. Однако для reltol менее 1e-3, abstol для состояния инициализировано в reltol * 1e-3. По мере выполнения моделирования абсолютный допуск для каждого состояния сбрасывается до максимального значения, которое до сих пор принималось за состояние, умноженного на относительный допуск для этого состояния. Таким образом, если состояние изменяется с 0 на 1 и reltol 1e-3, abstol инициализируется в 1e-6 и к концу моделирования достигает также 1e-3. Если состояние переходит из 0 в 1000, то abstol изменяется на 1.
Теперь, если состояние изменяется с 0 на 1 и reltol устанавливается на 1e-4, затем abstol инициализируется в 1e-7 и к концу моделирования достигает значения 1e-4.
Если вычисленное начальное значение для абсолютного допуска не подходит, можно определить соответствующее значение самостоятельно. Для определения соответствующего значения абсолютного допуска может потребоваться выполнить моделирование несколько раз. Можно также указать, должен ли абсолютный допуск адаптироваться аналогично его auto путем включения или отключения AutoScaleAbsTol параметр. Дополнительные сведения см. в разделе Автоматическое масштабирование абсолютного допуска.
Несколько блоков позволяют задать абсолютные значения допуска для решения состояний модели, которые они вычисляют или которые определяют их вывод:
Значения абсолютного допуска, заданные для этих блоков, переопределяют глобальные настройки в диалоговом окне «Параметры конфигурации». Можно переопределить глобальную настройку, если, например, глобальная настройка не обеспечивает достаточного контроля ошибок для всех состояний модели, поскольку они сильно различаются по величине. Абсолютный допуск блока можно задать равным:
auto
–1 (то же, что и auto)
positive scalar
real vector (имеющий размер, равный количеству соответствующих непрерывных состояний в блоке)
Если вы решили установить абсолютный допуск, помните, что слишком низкое значение приводит к тому, что решатель выполняет слишком много шагов вблизи значений состояния, близкого к нулю. В результате моделирование происходит медленнее.
С другой стороны, если установить слишком высокий абсолютный допуск, результаты могут быть неточными, поскольку одно или несколько непрерывных состояний в модели приближаются к нулю.
После завершения моделирования можно проверить точность результатов, уменьшив абсолютный допуск и снова запустив моделирование. Если результаты этих двух симуляций удовлетворительно близки, то можно почувствовать уверенность в их точности.