Категоризация точек запроса на основе их расстояния до точек в обучающем наборе данных может быть простым, но эффективным способом классификации новых точек. Для определения расстояния можно использовать различные метрики, описанные ниже. Использовать pdist2 для поиска расстояния между набором данных и точками запроса.
Учитывая матрицу X данных mx-на-n, которая обрабатывается как векторы строк mx (1-на-n) x1, x2,..., xmx и матрица данных my-на-n Y, которая обрабатывается как мои векторы строк y1, y2,..., ymy, различные расстояния между вектором xs и yt определяются следующим образом:
Евклидово расстояние
− yt) ′.
Евклидово расстояние - частный случай расстояния Минковского, где p = 2.
Стандартизированное евклидово расстояние
xs − yt) ′,
где V - диагональная матрица n-на-n, j-й диагональный элемент которой равен (S (j)) 2, где S - вектор масштабных коэффициентов для каждой размерности.
Расстояние Махаланобиса
xs − yt) ′,
где C - ковариационная матрица.
Расстояние между городскими кварталами
Расстояние городского блока - частный случай расстояния Минковского, где p = 1.
Минковская дистанция
Для особого случая p = 1 расстояние Минковского даёт расстояние городского блока. Для частного случая p = 2 расстояние Минковского даёт евклидово расстояние. Для частного случая p = ∞ дистанция Минковского даёт дистанцию Чебычева.
Чебычевская дистанция
ytj |}.
Дистанция Чебычева - частный случай дистанции Минковского, где p = ∞.
Расстояние косинуса
yty′t)).
Корреляционное расстояние
(yt−y¯t) ′,
где
и
Расстояние хэмминга
/n).
Расстояние Яккарда
∪ (ytj≠0)].
Расстояние Спирмена
(rt−r¯t) ′,
где
Учитывая набор X из n точек и функцию расстояния, поиск k-ближайшего соседа (kNN) позволяет найти k ближайших точек в X к точке запроса или набору точек Y. Методика поиска kNN и алгоритмы на основе kNN широко используются в качестве правил эталонного обучения. Относительная простота метода поиска kNN позволяет легко сравнивать результаты из других методов классификации с результатами kNN. Метод использовался в различных областях, таких как:
биоинформатика
обработка изображений и сжатие данных
извлечение документов
компьютерное зрение
мультимедийная база данных
анализ маркетинговых данных
Вы можете использовать поиск kNN для других алгоритмов машинного обучения, таких как:
Классификация kNN
локальная взвешенная регрессия
отсутствие вменения и интерполяции данных
оценка плотности
Также можно использовать поиск kNN с множеством функций дистанционного обучения, таких как кластеризация K-means.
Напротив, для положительного реального значения r, rangesearch находит все точки в X которые находятся на расстоянии r каждой точки в Y. Этот поиск с фиксированным радиусом тесно связан с поиском kNN, поскольку он поддерживает одинаковые метрики расстояния и классы поиска и использует одни и те же алгоритмы поиска.
Если входные данные соответствуют любому из следующих критериев, knnsearch использует метод исчерпывающего поиска по умолчанию для поиска k-ближайших соседей:
Количество столбцов X составляет более 10.
X разрежен.
Метрика расстояния:
'seuclidean'
'mahalanobis'
'cosine'
'correlation'
'spearman'
'hamming'
'jaccard'
Пользовательская функция расстояния
knnsearch также использует метод исчерпывающего поиска, если объектом поиска является ExhaustiveSearcher объект модели. Метод исчерпывающего поиска определяет расстояние от каждой точки запроса до каждой точки в X, ранжирует их в порядке возрастания и возвращает k точек с наименьшими расстояниями. Например, эта диаграмма показывает k = 3 ближайших соседей.
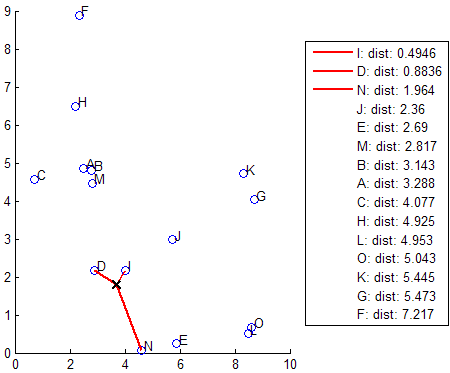
Если входные данные соответствуют всем следующим критериям, knnsearch создает дерево Kd по умолчанию для поиска k-ближайших соседей:
Количество столбцов X менее 10.
X не разрежен.
Метрика расстояния:
'euclidean' (по умолчанию)
'cityblock'
'minkowski'
'chebychev'
knnsearch также использует дерево Kd, если объектом поиска является KDTreeSearcher объект модели.
Kd-trees делят данные на узлы максимум с BucketSize (по умолчанию - 50) точек на узел на основе координат (в отличие от категорий). Следующие диаграммы иллюстрируют эту концепцию с использованием patch объекты для цветового кода различных «сегментов».
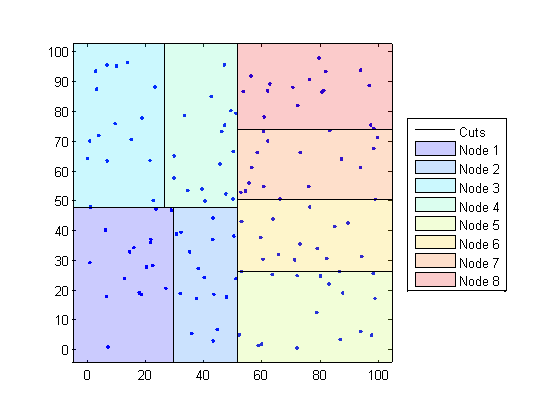
Если требуется найти k-ближайших соседей к заданной точке запроса, knnsearch выполняет следующее:
Определяет узел, которому принадлежит точка запроса. В следующем примере точка запроса (32,90) принадлежит узлу 4.
Находит ближайшие k точек в пределах этого узла и его расстояние до точки запроса. В следующем примере точки в красных кругах равноудалены от точки запроса и являются ближайшими точками к точке запроса в узле 4.
Выбирает все другие узлы, имеющие любую область, которая находится в пределах одного и того же расстояния в любом направлении от точки запроса до k-ой ближайшей точки. В этом примере только узел 3 перекрывает сплошной черный круг, центрированный в точке запроса с радиусом, равным расстоянию до ближайших точек в узле 4.
Поиск в узлах этого диапазона любых точек, расположенных ближе к точке запроса. В следующем примере точка в красном квадрате немного ближе к точке запроса, чем точки в узле 4.
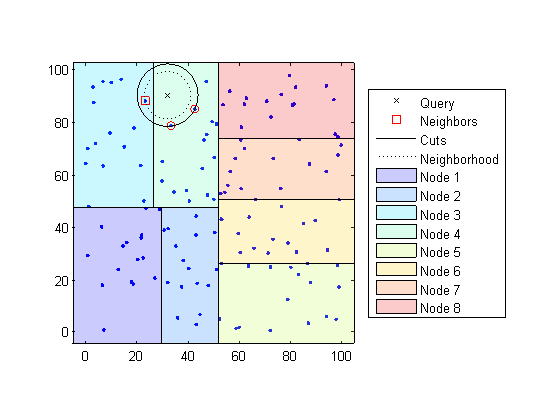
Использование дерева Kd для больших наборов данных с менее чем 10 измерениями (столбцами) может быть гораздо более эффективным, чем использование метода исчерпывающего поиска, как knnsearch необходимо вычислить только подмножество расстояний. Чтобы максимизировать эффективность Kd-деревьев, используйте KDTreeSearcher модель.
В основном, объекты модели являются удобным способом хранения информации. Связанные модели имеют одинаковые свойства со значениями и типами, соответствующими указанному методу поиска. Помимо хранения информации в моделях, можно выполнять определенные действия с моделями.
Можно эффективно выполнять k-ближайший поиск соседей в модели поиска с помощью knnsearch. Также можно выполнить поиск всех соседей в пределах указанного радиуса с помощью модели поиска и rangesearch. Кроме того, существуют родовые knnsearch и rangesearch функции, выполняющие поиск без создания или использования модели.
Чтобы определить, какой тип модели и метод поиска лучше всего подходят для данных, рассмотрим следующее:
У ваших данных много столбцов, скажем, больше 10? ExhaustiveSearcher модель может работать лучше.
Ваши данные редки? Используйте ExhaustiveSearcher модель.
Использовать одну из этих метрик расстояния для поиска ближайших соседей? Используйте ExhaustiveSearcher модель.
'seuclidean'
'mahalanobis'
'cosine'
'correlation'
'spearman'
'hamming'
'jaccard'
Пользовательская функция расстояния
Ваш набор данных огромен (но содержит менее 10 столбцов)? Используйте KDTreeSearcher модель.
Вы ищете ближайшие соседи для большого количества точек запроса? Используйте KDTreeSearcher модель.
В этом примере показано, как классифицировать данные запроса по:
Выращивание дерева Kd
Выполнение k поиска ближайшего соседа с использованием выращенного дерева.
Назначение каждой точки запроса класса с наибольшим представлением среди соответствующих ближайших соседей.
Классифицируйте новую точку на основе последних двух столбцов данных радужки Фишера. Использование только двух последних столбцов упрощает печать.
load fisheriris x = meas(:,3:4); gscatter(x(:,1),x(:,2),species) legend('Location','best')

Постройте график новой точки.
newpoint = [5 1.45]; line(newpoint(1),newpoint(2),'marker','x','color','k',... 'markersize',10,'linewidth',2)

Подготовка соседней поисковой модели Kd-дерева.
Mdl = KDTreeSearcher(x)
Mdl =
KDTreeSearcher with properties:
BucketSize: 50
Distance: 'euclidean'
DistParameter: []
X: [150x2 double]
Mdl является KDTreeSearcher модель. По умолчанию метрикой расстояния, используемой для поиска соседей, является евклидово расстояние.
Найдите 10 точек выборки, ближайших к новой точке.
[n,d] = knnsearch(Mdl,newpoint,'k',10); line(x(n,1),x(n,2),'color',[.5 .5 .5],'marker','o',... 'linestyle','none','markersize',10)

Похоже, что knnsearch нашел только ближайшие восемь соседей. Фактически, этот конкретный набор данных содержит повторяющиеся значения.
x(n,:)
ans = 10×2
5.0000 1.5000
4.9000 1.5000
4.9000 1.5000
5.1000 1.5000
5.1000 1.6000
4.8000 1.4000
5.0000 1.7000
4.7000 1.4000
4.7000 1.4000
4.7000 1.5000
Сделайте оси равными, чтобы вычисленные расстояния соответствовали видимым расстояниям на оси графика, и увеличьте масштаб изображения, чтобы лучше видеть соседей.
xlim([4.5 5.5]);
ylim([1 2]);
axis square
Найдите виды 10 соседей.
tabulate(species(n))
Value Count Percent virginica 2 20.00% versicolor 8 80.00%
Используя правило, основанное на большинстве голосов 10 ближайших соседей, можно классифицировать эту новую точку как versicolor.
Визуально идентифицировать соседей, проведя вокруг них круг. Определите центр и диаметр окружности на основе местоположения новой точки.
ctr = newpoint - d(end); diameter = 2*d(end); % Draw a circle around the 10 nearest neighbors. h = rectangle('position',[ctr,diameter,diameter],... 'curvature',[1 1]); h.LineStyle = ':';

Используя тот же набор данных, найдите 10 ближайших соседей к трем новым точкам.
figure newpoint2 = [5 1.45;6 2;2.75 .75]; gscatter(x(:,1),x(:,2),species) legend('location','best') [n2,d2] = knnsearch(Mdl,newpoint2,'k',10); line(x(n2,1),x(n2,2),'color',[.5 .5 .5],'marker','o',... 'linestyle','none','markersize',10) line(newpoint2(:,1),newpoint2(:,2),'marker','x','color','k',... 'markersize',10,'linewidth',2,'linestyle','none')

Найдите виды 10 ближайших соседей для каждой новой точки.
tabulate(species(n2(1,:)))
Value Count Percent virginica 2 20.00% versicolor 8 80.00%
tabulate(species(n2(2,:)))
Value Count Percent virginica 10 100.00%
tabulate(species(n2(3,:)))
Value Count Percent
versicolor 7 70.00%
setosa 3 30.00%
Дополнительные примеры использования knnsearch методы и функции см. в отдельных справочных страницах.
В этом примере показано, как найти индексы трех ближайших наблюдений в X к каждому наблюдению в Y относительно расстояния хи-квадрат. Эта метрика расстояния используется при анализе соответствия, особенно в экологических приложениях.
Случайная генерация нормально распределенных данных в две матрицы. Количество строк может варьироваться, но число столбцов должно быть равным. В этом примере для печати используются 2-D данные.
rng(1) % For reproducibility X = randn(50,2); Y = randn(4,2); h = zeros(3,1); figure h(1) = plot(X(:,1),X(:,2),'bx'); hold on h(2) = plot(Y(:,1),Y(:,2),'rs','MarkerSize',10); title('Heterogeneous Data')

Строки X и Y соответствуют наблюдениям, а столбцами являются, в общем, измерения (например, предикторы).
Расстояние хи-квадрат между j-мерными точками x и z равно
xj-zj) 2,
где - вес, связанный с размерностью j.
Выберите веса для каждого размера и задайте функцию расстояния хи-квадрат. Функция расстояния должна:
Взять в качестве входных аргументов одну строку X, например, xи матрица Z.
Выдержать сравнение x к каждой строке Z.
Возврат вектора D длины , где - количество строк Z. Каждый элемент D - расстояние между наблюдением, соответствующим x и наблюдения, соответствующие каждой строке Z.
w = [0.4; 0.6]; chiSqrDist = @(x,Z)sqrt((bsxfun(@minus,x,Z).^2)*w);
В этом примере для иллюстрации используются произвольные веса.
Найдите индексы трех ближайших наблюдений в X к каждому наблюдению в Y.
k = 3; [Idx,D] = knnsearch(X,Y,'Distance',chiSqrDist,'k',k);
idx и D представляют собой матрицы 4 на 3.
idx(j,1) - индекс строки ближайшего наблюдения в X к наблюдению j Y, и D(j,1) это их расстояние.
idx(j,2) - индекс строки следующего ближайшего наблюдения в X к наблюдению j Y, и D(j,2) это их расстояние.
И так далее.
Определите ближайшие наблюдения на графике.
for j = 1:k h(3) = plot(X(Idx(:,j),1),X(Idx(:,j),2),'ko','MarkerSize',10); end legend(h,{'\texttt{X}','\texttt{Y}','Nearest Neighbor'},'Interpreter','latex') title('Heterogeneous Data and Nearest Neighbors') hold off

Несколько наблюдений Y поделиться ближайшими соседями.
Убедитесь, что метрика расстояния хи-квадрат эквивалентна метрике евклидова расстояния, но с необязательным параметром масштабирования.
[IdxE,DE] = knnsearch(X,Y,'Distance','seuclidean','k',k, ... 'Scale',1./(sqrt(w))); AreDiffIdx = sum(sum(Idx ~= IdxE))
AreDiffIdx = 0
AreDiffDist = sum(sum(abs(D - DE) > eps))
AreDiffDist = 0
Индексы и расстояния между двумя реализациями трех ближайших соседей практически эквивалентны.
ClassificationKNN классификационная модель позволяет:
Подготовьте данные для классификации в соответствии с процедурой, описанной в разделе Шаги в контролируемом обучении. Затем создайте классификатор с помощью fitcknn.
В этом примере показано, как построить k-ближайший классификатор соседей для данных радужки Фишера.
Загрузите данные радужки Фишера.
load fisheriris X = meas; % Use all data for fitting Y = species; % Response data
Создание классификатора с помощью fitcknn.
Mdl = fitcknn(X,Y)
Mdl =
ClassificationKNN
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
Distance: 'euclidean'
NumNeighbors: 1
Properties, Methods
Классификатор k-ближайших соседей по умолчанию использует только один ближайший сосед. Часто классификатор более надежен с большим количеством соседей, чем это.
Изменение размера окрестности Mdl кому 4, означающее, что Mdl классифицирует с использованием четырех ближайших соседей.
Mdl.NumNeighbors = 4;
В этом примере показано, как проверить качество k-ближайшего классификатора соседей с помощью повторного замещения и перекрестной проверки.
Создайте KNN-классификатор для данных радужки Фишера, как в Construct KNN Classifier.
load fisheriris X = meas; Y = species; rng(10); % For reproducibility Mdl = fitcknn(X,Y,'NumNeighbors',4);
Проверьте потерю повторного замещения, которая по умолчанию является долей ошибочных классификаций из прогнозов Mdl. (Для получения информации о стоимости по умолчанию, весах или приорах см. раздел loss.).
rloss = resubLoss(Mdl)
rloss = 0.0400
Классификатор неправильно прогнозирует 4% данных обучения.
Создайте из модели перекрестно проверенный классификатор.
CVMdl = crossval(Mdl);
Проверьте потерю перекрестной проверки, которая является средней потерей каждой модели перекрестной проверки при прогнозировании данных, которые не используются для обучения.
kloss = kfoldLoss(CVMdl)
kloss = 0.0333
Точность перекрестной классификации напоминает точность повторного замещения. Поэтому можно ожидать Mdl для неправильной классификации приблизительно 4% новых данных, предполагая, что новые данные имеют примерно такое же распределение, что и данные обучения.
В этом примере показано, как предсказать классификацию для k-ближайшего классификатора соседей.
Создайте KNN-классификатор для данных радужки Фишера, как в Construct KNN Classifier.
load fisheriris X = meas; Y = species; Mdl = fitcknn(X,Y,'NumNeighbors',4);
Предсказать классификацию среднего цветка.
flwr = mean(X); % an average flower
flwrClass = predict(Mdl,flwr)flwrClass = 1x1 cell array
{'versicolor'}
В этом примере показано, как изменить k-ближайший классификатор соседей.
Создайте KNN-классификатор для данных радужки Фишера, как в Construct KNN Classifier.
load fisheriris X = meas; Y = species; Mdl = fitcknn(X,Y,'NumNeighbors',4);
Измените модель для использования трех ближайших соседей, а не одного ближайшего соседа по умолчанию.
Mdl.NumNeighbors = 3;
Сравните прогнозы повторного замещения и потери перекрестной проверки с новым количеством соседей.
loss = resubLoss(Mdl)
loss = 0.0400
rng(10); % For reproducibility CVMdl = crossval(Mdl,'KFold',5); kloss = kfoldLoss(CVMdl)
kloss = 0.0333
В этом случае модель с тремя соседями имеет те же потери, что и модель с четырьмя соседями (см. Анализ качества KNN-классификатора).
Измените модель, чтобы использовать расстояние косинуса вместо значения по умолчанию, и проверьте потери. Чтобы использовать расстояние косинуса, необходимо воссоздать модель с помощью метода исчерпывающего поиска.
CMdl = fitcknn(X,Y,'NSMethod','exhaustive','Distance','cosine'); CMdl.NumNeighbors = 3; closs = resubLoss(CMdl)
closs = 0.0200
Теперь в классификаторе меньше ошибок повторного предоставления, чем раньше.
Проверьте качество версии новой модели, прошедшей перекрестную проверку.
CVCMdl = crossval(CMdl); kcloss = kfoldLoss(CVCMdl)
kcloss = 0.0200
CVCMdl имеет лучшую перекрестную проверенную потерю, чем CVMdl. Однако в целом, улучшение ошибки повторного замещения не обязательно дает модель с лучшими прогнозами тестовой выборки.
ClassificationKNN | ExhaustiveSearcher | fitcknn | KDTreeSearcher