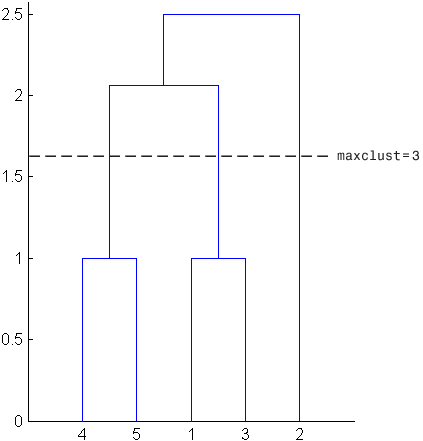Иерархическая кластеризация группирует данные в различных масштабах путем создания дерева кластера или дендрограммы. Дерево представляет собой не один набор кластеров, а многоуровневую иерархию, где кластеры на одном уровне соединяются как кластеры на следующем уровне. Это позволяет определить уровень или масштаб кластеризации, наиболее подходящий для приложения. Функция clusterdata поддерживает агломерированную кластеризацию и выполняет все необходимые для вас шаги. Он включает в себя pdist, linkage, и cluster функции, которые можно использовать отдельно для более подробного анализа. dendrogram функция отображает дерево кластера.
Для выполнения агрегированного иерархического кластерного анализа набора данных с использованием функций Statistics and Machine Learning Toolbox™ выполните следующую процедуру:
Найдите сходство или различие между каждой парой объектов в наборе данных. На этом шаге вычисляется расстояние между объектами с помощью pdist функция. pdist функция поддерживает множество различных способов вычисления этого измерения. Дополнительные сведения см. в разделе Показатели подобия.
Сгруппируйте объекты в двоичное иерархическое дерево кластера. На этом шаге вы связываете пары объектов, которые находятся в непосредственной близости, с помощью linkage функция. linkage функция использует информацию о расстоянии, сгенерированную на этапе 1, для определения близости объектов друг к другу. Поскольку объекты спарены в двоичные кластеры, вновь сформированные кластеры группируются в большие кластеры до тех пор, пока не будет сформировано иерархическое дерево. Дополнительную информацию см. в разделе Связи.
Определите, где разделять иерархическое дерево на кластеры. На этом шаге используется cluster функция для удаления ветвей из нижней части иерархического дерева и назначения всех объектов под каждым вырезом одному кластеру. При этом создается раздел данных. cluster функция может создавать эти кластеры, обнаруживая естественные группировки в иерархическом дереве или отсекая иерархическое дерево в произвольной точке.
В следующих разделах содержится дополнительная информация о каждом из этих шагов.
Примечание
Функция clusterdata выполняет все необходимые для вас шаги. Вам не нужно выполнять pdist, linkage, или cluster функционирует отдельно.
Вы используете pdist для вычисления расстояния между каждой парой объектов в наборе данных. Для набора данных, состоящего из m объектов, в наборе данных имеются пары m * (m - 1 )/2. Результат этого вычисления обычно известен как матрица расстояния или разнородности.
Существует множество способов вычисления этой информации о расстояниях. По умолчанию pdist функция вычисляет евклидово расстояние между объектами; однако можно указать один из нескольких вариантов. Посмотрите pdist для получения дополнительной информации.
Примечание
Можно дополнительно нормализовать значения в наборе данных перед вычислением информации о расстояниях. В реальном наборе данных переменные могут измеряться по разным масштабам. Например, одна переменная может измерять показатели теста Intelligence Quotient (IQ), а другая переменная может измерять окружность головы. Эти расхождения могут исказить расчеты близости. Использование zscore можно преобразовать все значения в наборе данных, чтобы использовать одну и ту же пропорциональную шкалу. Посмотрите zscore для получения дополнительной информации.
Например, рассмотрим набор данных, X, состоит из пяти объектов, где каждый объект является набором координат x, y.
1:1 объекта, 2
Объект 2: 2.5, 4.5
3:2 объекта, 2
4:4, 1,5 объекта
5:4, 2,5 объекта
Этот набор данных можно определить как матрицу.
rng default; % For reproducibility X = [1 2;2.5 4.5;2 2;4 1.5;... 4 2.5];
и передать его в pdist. pdist функция вычисляет расстояние между объектом 1 и объектом 2, объектом 1 и объектом 3 и т.д. до тех пор, пока не будут вычислены расстояния между всеми парами. На следующем рисунке эти объекты отображаются на графике. Евклидово расстояние между объектом 2 и объектом 3 показано для иллюстрации одной интерпретации расстояния.
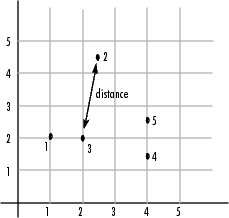
pdist функция возвращает эту информацию о расстоянии в векторе, Y, где каждый элемент содержит расстояние между парой объектов.
Y = pdist(X)
Y = 1×10
2.9155 1.0000 3.0414 3.0414 2.5495 3.3541 2.5000 2.0616 2.0616 1.0000
Для упрощения просмотра взаимосвязи между информацией о расстояниях, генерируемой pdist и объекты в исходном наборе данных, можно переформатировать вектор расстояния в матрицу, используя squareform функция. В этой матрице элементы i, j соответствуют расстоянию между объектом i и объектом j в исходном наборе данных. В следующем примере элемент 1,1 представляет расстояние между объектом 1 и самим собой (которое равно нулю). Элемент 1,2 представляет расстояние между объектом 1 и объектом 2 и т.д.
squareform(Y)
ans = 5×5
0 2.9155 1.0000 3.0414 3.0414
2.9155 0 2.5495 3.3541 2.5000
1.0000 2.5495 0 2.0616 2.0616
3.0414 3.3541 2.0616 0 1.0000
3.0414 2.5000 2.0616 1.0000 0
После вычисления близости между объектами в наборе данных можно определить, как объекты в наборе данных должны быть сгруппированы в кластеры, используя linkage функция. linkage функция принимает информацию о расстоянии, генерируемую pdist и связывает пары объектов, близких друг к другу, в двоичные кластеры (кластеры, состоящие из двух объектов). linkage затем функция связывает эти вновь сформированные кластеры друг с другом и с другими объектами для создания больших кластеров до тех пор, пока все объекты в исходном наборе данных не будут связаны вместе в иерархическом дереве.
Например, учитывая вектор расстояния Y генерируется pdist из набора данных выборки координат x и y, linkage функция генерирует иерархическое дерево кластера, возвращая информацию о связях в матрице, Z.
Z = linkage(Y)
Z = 4×3
4.0000 5.0000 1.0000
1.0000 3.0000 1.0000
6.0000 7.0000 2.0616
2.0000 8.0000 2.5000
В этом выводе каждая строка идентифицирует связь между объектами или кластерами. Первые два столбца определяют связанные объекты. Третий столбец содержит расстояние между этими объектами. Для набора данных выборки координат x и y: linkage функция начинается с группирования объектов 4 и 5, которые имеют ближайшую близость (значение расстояния = 1,0000). linkage функция продолжается группировкой объектов 1 и 3, которые также имеют значение расстояния 1,0000.
Третья строка указывает, что linkage функция сгруппировала объекты 6 и 7. Если исходный набор данных образца содержал только пять объектов, то что такое объекты 6 и 7? Объект 6 является вновь сформированным двоичным кластером, созданным группировкой объектов 4 и 5. Когда linkage функция группирует два объекта в новый кластер, она должна присвоить кластеру уникальное значение индекса, начиная со значения m + 1, где m - количество объектов в исходном наборе данных. (Значения от 1 до m уже используются исходным набором данных.) Аналогично, объект 7 является кластером, образованным группировкой объектов 1 и 3.
linkage использует расстояния для определения порядка кластеризации объектов. Вектор расстояния Y содержит расстояния между исходными объектами, 1 через 5. Но связь также должна быть способна определять расстояния, связанные с созданными ею кластерами, такими как объекты 6 и 7. По умолчанию linkage использует метод, известный как одинарная связь. Однако существует ряд различных методов. См. раздел linkage для получения дополнительной информации.
В качестве окончательного кластера, linkage функция сгруппировала объект 8, вновь сформированный кластер, состоящий из объектов 6 и 7, с объектом 2 из исходного набора данных. Следующий рисунок графически иллюстрирует способ linkage группирует объекты в иерархию кластеров.
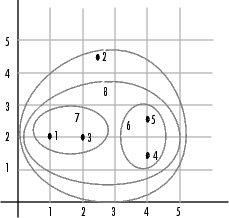
Иерархическое двоичное дерево кластера, созданное linkage функция наиболее легко понятна при графическом просмотре. Функция dendrogram отображает дерево следующим образом.
dendrogram(Z)

На рисунке числа вдоль горизонтальной оси представляют индексы объектов в исходном наборе данных. Связи между объектами представлены в виде U-образных линий вверх-вниз. Высота U указывает расстояние между объектами. Например, линия связи, представляющая кластер, содержащий объекты 1 и 3, имеет высоту 1. Связь, представляющая кластер, который группирует объект 2 вместе с объектами 1, 3, 4 и 5 (которые уже сгруппированы как объект 8), имеет высоту 2,5. Высота представляет расстояние linkage вычисляет между объектами 2 и 8. Для получения дополнительной информации о создании диаграммы дендрограммы см. dendrogram справочная страница.
После связывания объектов в наборе данных с иерархическим деревом кластера можно проверить, что расстояния (то есть высоты) в дереве точно отражают исходные расстояния. Кроме того, может потребоваться исследовать естественные деления, существующие между связями между объектами. Функции статистики и инструментария машинного обучения доступны для обеих задач, как описано в следующих разделах.
В иерархическом дереве кластера любые два объекта в исходном наборе данных в конечном счете связаны друг с другом на некотором уровне. Высота звена представляет расстояние между двумя кластерами, содержащими эти два объекта. Эта высота известна как кофенетическое расстояние между двумя объектами. Один из способов измерения качества дерева кластера, созданного linkage функция отражает ваши данные для сравнения кофенетических расстояний с исходными данными расстояния, сгенерированными pdist функция. Если кластеризация допустима, связь объектов в дереве кластера должна иметь сильную корреляцию с расстояниями между объектами в векторе расстояний. cophenet функция сравнивает эти два набора значений и вычисляет их корреляцию, возвращая значение, называемое коэффициентом кофенетической корреляции. Чем ближе значение коэффициента кофенетической корреляции к 1, тем точнее решение кластеризации отражает ваши данные.
Коэффициент кофенетической корреляции можно использовать для сравнения результатов кластеризации одного и того же набора данных с использованием различных методов расчета расстояния или алгоритмов кластеризации. Например, можно использовать cophenet для оценки кластеров, созданных для набора данных выборки.
c = cophenet(Z,Y)
c = 0.8615
Z - матрица, выводимая linkage функции и Y - вектор расстояния, выводимый pdist функция.
Выполнить pdist снова в том же наборе данных, на этот раз указывая метрику городского блока. После запуска linkage функция на этом новом pdist вывод с использованием метода средней связи, вызов cophenet для оценки решения кластеризации.
Y = pdist(X,'cityblock'); Z = linkage(Y,'average'); c = cophenet(Z,Y)
c = 0.9047
Коэффициент кофенетической корреляции показывает, что использование другого метода расстояния и связи создает дерево, которое представляет исходные расстояния несколько лучше.
Одним из способов определения естественных делений кластера в наборе данных является сравнение высоты каждого звена в дереве кластера с высотами соседних звеньев под ним в дереве.
Связь, высота которой приблизительно равна высоте связей, расположенных ниже, указывает на отсутствие отдельных делений между объектами, соединенными на этом уровне иерархии. Говорят, что эти связи демонстрируют высокий уровень согласованности, поскольку расстояние между соединяемыми объектами приблизительно равно расстоянию между содержащимися в них объектами.
С другой стороны, звено, высота которого заметно отличается от высоты звеньев ниже, указывает на то, что объекты, соединенные на этом уровне в дереве кластера, значительно дальше друг от друга, чем их компоненты, когда они были соединены. Считается, что эта ссылка несовместима со ссылками под ней.
В кластерном анализе несогласованные ссылки могут указывать границу естественного деления в наборе данных. cluster функция использует количественную меру несогласованности, чтобы определить, где разделить набор данных на кластеры.
Следующая дендрограмма иллюстрирует противоречивые связи. Обратите внимание, как объекты в дендрограмме попадают в две группы, которые соединены связями на гораздо более высоком уровне в дереве. Эти ссылки противоречивы по сравнению со ссылками ниже них в иерархии.
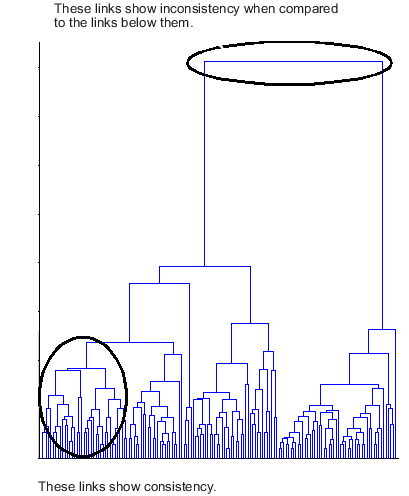
Относительная согласованность каждой линии связи в иерархическом дереве кластера может быть определена количественно и выражена как коэффициент несогласованности. Это значение сравнивает высоту ссылки в иерархии кластера со средней высотой ссылок под ней. Связи, объединяющие отдельные кластеры, имеют высокий коэффициент несогласованности; связи, которые объединяют невнятные кластеры, имеют низкий коэффициент несогласованности.
Чтобы создать список коэффициентов несогласованности для каждой связи в дереве кластера, используйте inconsistent функция. По умолчанию inconsistent функция сравнивает каждое звено в иерархии кластера со смежными звеньями, которые ниже его на два уровня в иерархии кластера. Это называется глубиной сравнения. Можно также задать другие глубины. Объекты в нижней части дерева кластера, называемые конечными узлами, которые не имеют дополнительных объектов под ними, имеют нулевой коэффициент несогласованности. Кластеры, объединяющие два листа, также имеют нулевой коэффициент несогласованности.
Например, можно использовать inconsistent для вычисления значений несогласованности для связей, созданных linkage функция в связях.
Сначала повторно вычислите значения расстояния и связей, используя настройки по умолчанию.
Y = pdist(X); Z = linkage(Y);
Далее используйте inconsistent для вычисления значений несоответствия.
I = inconsistent(Z)
I = 4×4
1.0000 0 1.0000 0
1.0000 0 1.0000 0
1.3539 0.6129 3.0000 1.1547
2.2808 0.3100 2.0000 0.7071
inconsistent функция возвращает данные о связях в матрице (m-1) -by-4, столбцы которой описаны в следующей таблице.
| Колонка | Описание |
|---|---|
1 | Среднее значение высоты всех звеньев, включенных в расчет |
2 | Стандартное отклонение всех звеньев, включенных в расчет |
3 | Количество ссылок, включенных в расчет |
4 | Коэффициент несогласованности |
В примере выходных данных первая строка представляет связь между объектами 4 и 5. Этому кластеру присваивается индекс 6 linkage функция. Поскольку и 4, и 5 являются конечными узлами, коэффициент несогласованности для кластера равен нулю. Вторая строка представляет связь между объектами 1 и 3, оба из которых также являются конечными узлами. Этому кластеру присваивается индекс 7 функцией связывания.
Третья строка оценивает связь, которая соединяет эти два кластера, объекты 6 и 7. (Этому новому кластеру присвоен индекс 8 в linkage выход). Столбец 3 указывает, что при расчете учитываются три связи: сама связь и две связи непосредственно под ней в иерархии. Столбец 1 представляет среднее значение высоты этих звеньев. inconsistent функция использует информацию о высоте, выводимую linkage для вычисления среднего значения. Столбец 2 представляет стандартное отклонение между звеньями. Последний столбец содержит значение несогласованности для этих ссылок, 1.1547. Это разность между текущей высотой звена и средним значением, нормализованным стандартным отклонением.
(2.0616 - 1.3539) / .6129
ans = 1.1547
На следующем рисунке показаны ссылки и высоты, включенные в этот расчет.
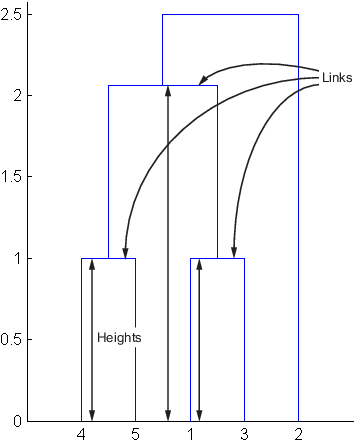
Примечание
На предыдущем рисунке нижний предел на оси y установлен равным 0 для отображения высоты звеньев. Установка нижнего предела равным 0, выберите Axes Properties в меню Правка (Edit) перейдите на вкладку Ось Y (Y Axis) и введите 0 в поле непосредственно справа от Y Limits.
Строка 4 в выходной матрице описывает связь между объектом 8 и объектом 2. Столбец 3 указывает, что в этот расчет включены две ссылки: сама ссылка и ссылка непосредственно под ней в иерархии. Коэффициент несогласованности для этой линии связи равен 0,7071.
На следующем рисунке показаны ссылки и высоты, включенные в данный расчет.
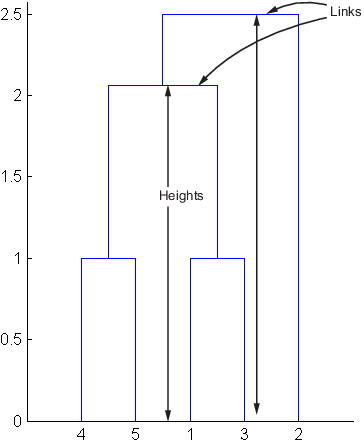
После создания иерархического дерева двоичных кластеров можно обрезать дерево для разделения данных на кластеры с помощью cluster функция. cluster функция позволяет создавать кластеры двумя способами, как описано в следующих разделах.
Иерархическое дерево кластеров может естественным образом разделить данные на отдельные, хорошо разделенные кластеры. Это может быть особенно очевидно на диаграмме дендрограммы, созданной на основе данных, где группы объектов плотно упакованы в определенных областях, а не в других. Коэффициент несогласованности связей в дереве кластера может идентифицировать эти деления, где сходства между объектами резко изменяются. (Дополнительные сведения о коэффициенте несогласованности см. в разделе Проверка дерева кластера.) Это значение можно использовать для определения местоположения cluster создает границы кластера.
Например, при использовании cluster функция группирования набора данных выборки в кластеры, определяющая пороговое значение коэффициента несогласованности 1.2 как значение cutoff аргумент, cluster функция группирует все объекты в образце набора данных в один кластер. В этом случае ни одна из ссылок в иерархии кластера не имела коэффициента несогласованности больше, чем 1.2.
T = cluster(Z,'cutoff',1.2)T = 5×1
1
1
1
1
1
cluster функция выводит вектор, T, то есть того же размера, что и исходный набор данных. Каждый элемент в этом векторе содержит номер кластера, в который был помещен соответствующий объект из исходного набора данных.
При снижении порогового значения коэффициента несоответствия до 0.8, cluster функция делит набор данных выборки на три отдельных кластера.
T = cluster(Z,'cutoff',0.8)T = 5×1
3
2
3
1
1
Эти выходные данные указывают, что объекты 1 и 3 находятся в одном кластере, объекты 4 и 5 находятся в другом кластере, а объект 2 находится в своем собственном кластере.
Когда кластеры формируются таким образом, значение отсечки применяется к коэффициенту несогласованности. Эти кластеры могут, но не обязательно, соответствовать горизонтальному срезу по дендрограмме на определенной высоте. Если вы хотите кластеры, соответствующие горизонтальному срезу дендрограммы, вы можете использовать criterion чтобы указать, что отсечение должно основываться на расстоянии, а не на несогласованности, или можно указать количество кластеров непосредственно, как описано в следующем разделе.
Вместо того, чтобы позволить cluster функция создает кластеры, определяемые естественными разделами в наборе данных, можно указать количество кластеров, которые требуется создать.
Например, можно указать, что требуется cluster функция для разделения набора данных выборки на два кластера. В этом случае cluster функция создает один кластер, содержащий объекты 1, 3, 4 и 5, и другой кластер, содержащий объект 2.
T = cluster(Z,'maxclust',2)T = 5×1
2
1
2
2
2
Чтобы помочь визуализировать, как cluster функция определяет эти кластеры, на следующем рисунке показана дендрограмма иерархического дерева кластеров. Горизонтальная пунктирная линия пересекает две линии дендрограммы, соответствующие настройке 'maxclust' кому 2. Эти две строки разделяют объекты на два кластера: объекты ниже левой линии, а именно 1, 3, 4 и 5, принадлежат одному кластеру, в то время как объект ниже правой линии, а именно 2, принадлежит другому кластеру.
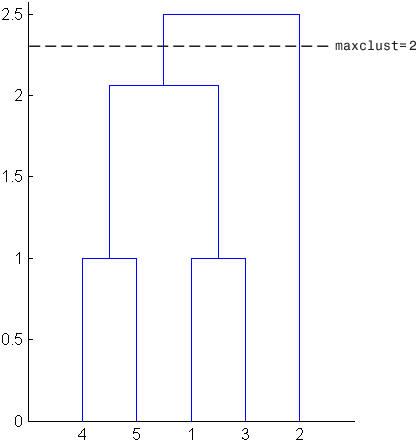
С другой стороны, если установить 'maxclust' кому 3функция кластера группирует объекты 4 и 5 в одном кластере, объекты 1 и 3 во втором кластере и объект 2 в третьем кластере. Следующая команда иллюстрирует это.
T = cluster(Z,'maxclust',3)T = 5×1
2
3
2
1
1
На этот раз, cluster функция отсекает иерархию в нижней точке, соответствующей горизонтальной линии, которая пересекает три линии дендрограммы на следующем рисунке.