Решение дифференциальных уравнений с помощью преобразования Лапласа

Решение дифференциальных уравнений с помощью преобразований Лапласа в символьных математических Toolbox™ с этим рабочим процессом. Простые примеры преобразования Лапласа см. в разделе laplace и ilaplace.

Определение: преобразование Лапласа

Преобразование Лапласа функции f (t)

$F (s)_{}^{} =∫0∞f (^{t)} e -$ tsdt.

Концепция: Использование символьных рабочих процессов

Символьные рабочие процессы содержат вычисления в натуральной символической форме, а не в числовой. Этот подход помогает понять свойства решения и использовать точные символьные значения. Числа подставляются вместо символьных переменных только в том случае, если требуется числовой результат или невозможно продолжить символьно. Дополнительные сведения см. в разделе Выбор числовой или символьной арифметики. Обычно этапы:

Объявить уравнения.
Решите уравнения.
Подстановочные значения.
Результаты графика.
Анализ результатов.

Рабочий процесс: решение RLC-цепи с помощью преобразования Лапласа

Объявить уравнения

Преобразование Лапласа можно использовать для решения дифференциальных уравнений с начальными условиями. Например, можно решить цепи сопротивление-индуктор-конденсатор (RLC), такие как эта схема.

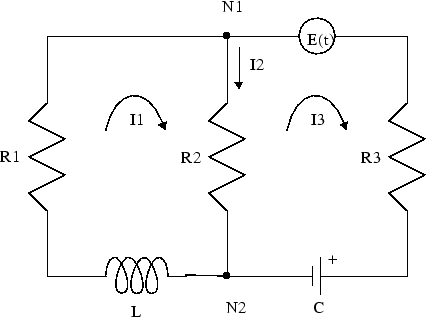
Сопротивления в Ом: _R1, _R2, _R3
Токи в ампере: _I1, _I2, _I3
Индуктивность в Генрихе: L
Емкость в фараде: C
Электродвижущая сила в вольтах: E (t)
Заряд в кулоне: Q (t)

Примените законы напряжения и тока Кирхгофа, чтобы получить дифференциальные уравнения для схемы RLC.

$\frac{_{}}{} \frac{_{}}{} \frac{}{} \frac{_{}_{}}{}_{dI1dt+R2LdQdt=R2−R1LI1} .$

$\frac{}{dQdt} \frac{=}{_{} {1R3}_{}} + R2 (\frac{E}{} (t) - \frac{_{}}{{1CQ}_{} (t_{)}})_{} +$ R2R3 + R2I1.

Объявите переменные. Поскольку физические величины имеют положительные значения, установите соответствующие допущения для переменных. Пусть E (t) - переменное напряжение 1 В.

syms L C I1(t) Q(t) s
R = sym('R%d',[1 3]);
assume([t L C R] > 0)
E(t) = 1*sin(t);        % Voltage = 1 V

Объявите дифференциальные уравнения.

dI1 = diff(I1,t);
dQ = diff(Q,t);
eqn1 = dI1 + (R(2)/L)*dQ == (R(2)-R(1))/L*I1
eqn2 = dQ == (1/(R(2)+R(3))*(E-Q/C)) + R(2)/(R(2)+R(3))*I1

eqn1(t) =
diff(I1(t), t) + (R2*diff(Q(t), t))/L == -(I1(t)*(R1 - R2))/L
eqn2(t) =
diff(Q(t), t) == (sin(t) - Q(t)/C)/(R2 + R3) + (R2*I1(t))/(R2 + R3)

Предположим, что начальный ток и заряд, _I0 и _Q0, являются 0. Объявите эти начальные условия.

cond1 = I1(0) == 0
cond2 = Q(0) == 0

cond1 =
I1(0) == 0
cond2 =
Q(0) == 0

Уравнения решения

Вычислить преобразование Лапласа eqn1 и eqn2.

eqn1LT = laplace(eqn1,t,s)
eqn2LT = laplace(eqn2,t,s)

eqn1LT =
s*laplace(I1(t), t, s) - I1(0) - (R2*(Q(0) - s*laplace(Q(t), t, s)))/L == ...
-((R1 - R2)*laplace(I1(t), t, s))/L
eqn2LT =
s*laplace(Q(t), t, s) - Q(0) == (R2*laplace(I1(t), t, s))/(R2 + R3) + ...
(C/(s^2 + 1) - laplace(Q(t), t, s))/(C*(R2 + R3))

Функция solve решает только для символьных переменных. Поэтому использовать solve, первая замена laplace(I1(t),t,s) и laplace(Q(t),t,s) с переменными I1_LT и Q_LT.

syms I1_LT Q_LT
eqn1LT = subs(eqn1LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn1LT =
I1_LT*s - I1(0) - (R2*(Q(0) - Q_LT*s))/L == -(I1_LT*(R1 - R2))/L

eqn2LT = subs(eqn2LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn2LT =
Q_LT*s - Q(0) == (I1_LT*R2)/(R2 + R3) - (Q_LT - C/(s^2 + 1))/(C*(R2 + R3))

Решить уравнения для I1_LT и Q_LT.

eqns = [eqn1LT eqn2LT];
vars = [I1_LT Q_LT];
[I1_LT, Q_LT] = solve(eqns,vars)

I1_LT =
(R2*Q(0) + L*I1(0) - C*R2*s + L*s^2*I1(0) + R2*s^2*Q(0) + C*L*R2*s^3*I1(0) + ...
C*L*R3*s^3*I1(0) + C*L*R2*s*I1(0) + C*L*R3*s*I1(0))/((s^2 + 1)*(R1 - R2 + L*s + ...
C*L*R2*s^2 + C*L*R3*s^2 + C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))
Q_LT =
(C*(R1 - R2 + L*s + L*R2*I1(0) + R1*R2*Q(0) + R1*R3*Q(0) - R2*R3*Q(0) + ...
L*R2*s^2*I1(0) + L*R2*s^3*Q(0) + L*R3*s^3*Q(0) + R1*R2*s^2*Q(0) + R1*R3*s^2*Q(0) - ...
R2*R3*s^2*Q(0) + L*R2*s*Q(0) + ...
L*R3*s*Q(0)))/((s^2 + 1)*(R1 - R2 + L*s + C*L*R2*s^2 + C*L*R3*s^2 + ...
                C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))

Вычислите _I1 и Q путем вычисления обратного преобразования Лапласа I1_LT и Q_LT. Упростите результат. Подавьте вывод, так как он длинный.

I1sol = ilaplace(I1_LT,s,t);
Qsol = ilaplace(Q_LT,s,t);
I1sol = simplify(I1sol);
Qsol = simplify(Qsol);

Подстановочные значения

Перед выводом на печать результата замените символьные переменные на числовые значения элементов цепи. Пусть R1 = 4 Ом , R2 = 2 Ом, R3 = 3 Ом , C = 1/4 F , L = 1,6 H , I1 ₍0) = 15 А и Q (0) = 2 C.

vars = [R L C I1(0) Q(0)];
values = [4 2 3 1.6 1/4 15 2];
I1sol = subs(I1sol,vars,values)
Qsol = subs(Qsol,vars,values)

I1sol =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - ...
        (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879) - (5*sin(t))/51
Qsol =
(4*sin(t))/51 - (5*cos(t))/51 + (107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + ...
        (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51

Результаты графика

Постройте график текущего I1sol и взимать плату Qsol. Отображение переходных и установившихся режимов с использованием двух различных временных интервалов: 0 ≤ t ≤ 10 и 5 ≤ t ≤ 25.

subplot(2,2,1)
fplot(I1sol,[0 10])                      
title('Current')
ylabel('I1(t)')
xlabel('t')

subplot(2,2,2)
fplot(Qsol,[0 10])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')

subplot(2,2,3)
fplot(I1sol,[5 25])                  
title('Current')
ylabel('I1(t)')
xlabel('t')
text(7,0.25,'Transient')
text(16,0.125,'Steady State')

subplot(2,2,4)
fplot(Qsol,[5 25])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')
text(7,0.25,'Transient')
text(15,0.16,'Steady State')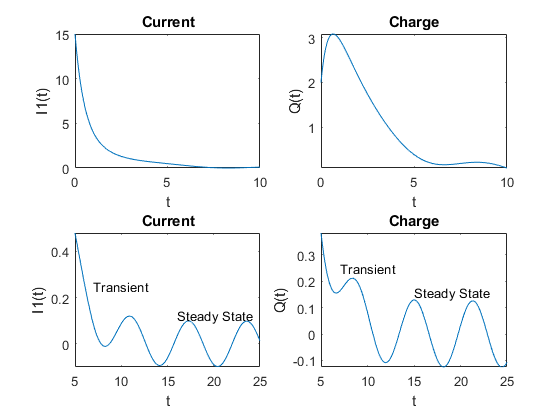

Анализ результатов

Первоначально ток и заряд уменьшаются экспоненциально. Однако в долгосрочной перспективе они являются колебательными. Это поведение называется «переходным» и «устойчивым состоянием» соответственно. С помощью символьного результата можно проанализировать свойства результата, что невозможно с помощью числовых результатов.

Визуальный осмотр I1sol и Qsol. Они представляют собой сумму терминов. Найдите термины с помощью children. Затем найдите вклады терминов, построив их график [0 15]. На графиках показаны переходные и установившиеся условия.

I1terms = children(I1sol);
Qterms = children(Qsol);

subplot(1,2,1)
fplot(I1terms,[0 15])
ylim([-2 2])
title('Current terms')

subplot(1,2,2)
fplot(Qterms,[0 15])
ylim([-2 2])
title('Charge terms')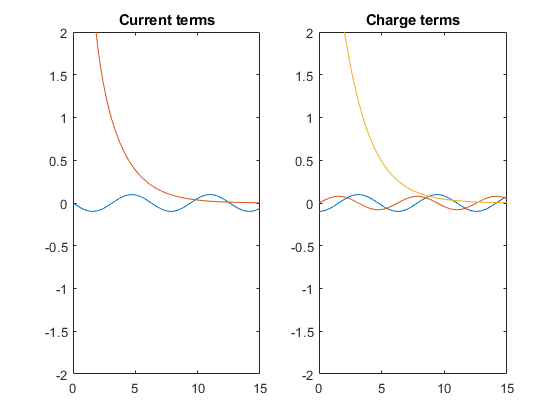

Графики показывают, что I1sol имеет член переходного и устойчивого состояния, в то время как Qsol имеет переходный и два установившихся условия. Визуальный осмотр, уведомление I1sol и Qsol имеют термин, содержащий exp функция. Предположим, что этот термин вызывает переходный экспоненциальный распад. Разделите переходные и установившиеся условия в I1sol и Qsol проверкой условий для exp использование has.

I1transient = I1terms(has(I1terms,'exp'))
I1steadystate = I1terms(~has(I1terms,'exp'))

I1transient =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879)
I1steadystate =
-(5*sin(t))/51

Аналогично, разделять Qsol в переходные и установившиеся условия. Этот результат демонстрирует, как символичные вычисления помогают проанализировать проблему.

Qtransient = Qterms(has(Qterms,'exp'))
Qsteadystate = Qterms(~has(Qterms,'exp'))

Qtransient =
(107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51
Qsteadystate =
[ -(5*cos(t))/51, (4*sin(t))/51]

Документация