Комбинированное проскальзывающее колесо 2DOF

Комбинированное колесо 2DOF скольжения с диском, барабаном или привязанным тормозом

Библиотека:
Блоксеть/колеса и шины Vehicle Dynamics

Описание

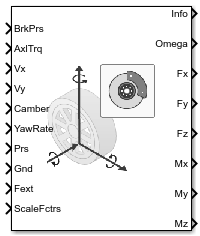
Блок Combined Slip Wheel 2DOF реализует продольное и боковое поведение колеса, характеризующегося магическими формулами ^{[1] и [2}]. Можно импортировать собственные данные о шинах или использовать наборы данных о встроенных шинах, предоставленные Глобальным центром моделирования производительности автомобилей (GCAPS). Использовать блок при моделировании трансмиссии и транспортного средства, где для определения ускорения, торможения и сопротивления качению колеса требуются низкочастотные силы движения шины и торможения. Блок подходит для применений, которые требуют комбинированного бокового скольжения, например, при исследованиях бокового движения и устойчивости к рысканию.

На основе крутящего момента трансмиссии, тормозного давления, высоты дороги, угла развала колеса и давления накачки блок определяет скорость вращения колеса, вертикальное движение, силы и моменты во всех шести степенях свободы (DOF). Используйте вертикальную степень свободы для изучения резонансов подвески шины из профиля дороги или движения шасси.

Используйте параметр Тип шины (Tire type) для выбора источника данных шины.

Цель Действие

Цель	Действие
Реализация формулы Magic с использованием эмпирических уравнений ^{[1] и [2}]. В уравнениях используются коэффициенты подгонки, соответствующие параметрам блока.	Обновите параметры блока с помощью коэффициентов фитинга из файла: Задайте для параметра «Тип шины» значение `External file`. На панели «Параметры колеса и шины» > «Шина» выберите «Выбрать файл». Выберите файл коэффициентов шины. Выберите Обновить значения маски из файла. В диалоговом окне с запросом подтверждения нажмите кнопку ОК. Блок обновляет параметры. Выберите «Применить».
Внедрение наборов данных по подогнанным шинам, предоставленных Глобальным центром моделирования производительности автомобилей (GCAPS).	Обновить соответствующие параметры блока с помощью данных о встроенных шинах GCAPS: Задайте тип шины, который требуется реализовать. Варианты включают в себя: `Light passenger car 205/60R15` `Mid-size passenger car 235/45R18` `Performance car 225/40R19` `SUV 265/50R20` `Light truck 275/65R18` `Commercial truck 295/75R22.5` Выберите Обновить применимые параметры шины с помощью значений типа шины. На вкладке «Параметры шины» блок обновляет применимые параметры, включая ширину колеса, радиус обода и массу колеса. Выберите «Применить».

Реализация формулы Magic с использованием эмпирических уравнений ^{[1] и [2}]. В уравнениях используются коэффициенты подгонки, соответствующие параметрам блока.

Обновите параметры блока с помощью коэффициентов фитинга из файла:

Задайте для параметра «Тип шины» значение External file.
На панели «Параметры колеса и шины» > «Шина» выберите «Выбрать файл».
Выберите файл коэффициентов шины.
Выберите Обновить значения маски из файла. В диалоговом окне с запросом подтверждения нажмите кнопку ОК. Блок обновляет параметры.
Выберите «Применить».

Внедрение наборов данных по подогнанным шинам, предоставленных Глобальным центром моделирования производительности автомобилей (GCAPS).

Обновить соответствующие параметры блока с помощью данных о встроенных шинах GCAPS:

Задайте тип шины, который требуется реализовать. Варианты включают в себя:
- Light passenger car 205/60R15
- Mid-size passenger car 235/45R18
- Performance car 225/40R19
- SUV 265/50R20
- Light truck 275/65R18
- Commercial truck 295/75R22.5
Выберите Обновить применимые параметры шины с помощью значений типа шины. На вкладке «Параметры шины» блок обновляет применимые параметры, включая ширину колеса, радиус обода и массу колеса.
Выберите «Применить».

Используйте параметр «Тип тормоза» для выбора тормоза.

Цель	Настройка типа тормоза
Без торможения	`None`
Реализовать тормоз, преобразующий давление тормозного цилиндра в тормозное усилие	`Disc`
Реализовать симплексный барабанный тормоз, преобразующий приложенную силу и геометрию тормоза в чистый тормозной момент	`Drum`
Реализовать таблицу поиска, которая является функцией скорости колеса и приложенного тормозного давления	`Mapped`

Динамика вращательного колеса

Блок вычисляет инерционный отклик колеса в зависимости от:

Потери оси
Крутящий момент тормоза и привода
Сопротивление качению шины
Контакт с землей через интерфейс шины-дорога

Для реализации магической формулы блок использует эти уравнения.

Вычисление	Уравнения
Продольная сила	Динамика шин и транспортных средств ^[2] уравнения 4.E9- 4.E57
Боковая сила - чистая боковая губа	Динамика шин и транспортных средств ^[2] уравнения 4.E19- 4.E30
Боковая сила - комбинированное скольжение	Динамика шин и транспортных средств ^[2] уравнения 4.E58- 4.E67
Вертикальная динамика	Динамика шин и транспортных средств ^[2] уравнения 4.E68, 4.E1, 4.E2a и 4.E2b
Опрокидывающаяся пара	Уравнение динамики шин и транспортных средств ^[2] 4.E69
Сопротивление качению	Усовершенствованная модель шины Magic Formula/Swift, которая может обрабатывать изменения давления [1] уравнение 6.1.2 Уравнение динамики шин и транспортных средств ^[2] 4.E70
Выравнивающий момент	Уравнение динамики шин и транспортных средств ^[2] 4.E31- 4.E49
Выравнивающий крутящий момент - комбинированное скольжение	Уравнение динамики шин и транспортных средств ^[2] 4.E71- 4.E78

Входной крутящий момент представляет собой сумму приложенного крутящего момента оси, тормозного момента и момента, возникающего из комбинированного крутящего момента шины.

$_{Ti} =_{} {Ta}_{} -_{}$ Tb + Td

На момент, возникающий от комбинированного крутящего момента шины, блок реализует тяговые силы колес и сопротивление качению с динамикой первого порядка. Сопротивление качению имеет постоянную времени, параметризованную в терминах длины релаксации.

$_{Td} (s) \frac{}{\frac{= 1_{|}}{_{}}}_{λ 'ReLes} +_{} 1_{(}$ Fx Re + My)

Если тормоза включены, блок определяет заблокированное или разблокированное состояние торможения на основе идеализированной модели трения сухого сцепления. На основе условия блокировки блок реализует эти модели трения и динамические модели.

Если	Условие блокировки	Модель трения	Динамическая модель
$\begin{array}{l} _{}_{}_{} ω\neq0orTS<\|Ti+Tf-ωb\| \end{array}$	Незапертый	$\begin{array}{l} _{Tf} =_{} \\ {Tkhere}_{,}_{Tk}_{=}_{} {FcRеффмкктанh}_{} [4 \\ _{(} -_{} {λ d}_{)]}_{Ts} \\ _{=} \frac{_{}^{}_{}^{} FcRеффмкsReff}{=_{2}^{} (_{}^{Ro3}} \end{array}$ − Ri3) 3 (Ro2 − Ri2)	$\overset{}{}_{}_{ω˙J=−ωb+Ti+To}$
$\begin{array}{l} _{}_{}_{} ω=0andTS\geq\|Ti+Tf-ωb\| \end{array}$	Запертый	$_{Tf} =_{}$ Ts	$ω=0$

Уравнения используют эти переменные.

ω	Угловая скорость колеса
a	Компонент силы, не зависящий от скорости
b	Компонент силы линейной скорости
c	Компонент силы квадратичной скорости
_Le	Длина релаксации шины
J	Момент инерции
_Мой	Крутящий момент сопротивления качению
_Ta	Крутящий момент оси вокруг оси вращения колеса
_TB	Тормозной момент
_Td	Комбинированный крутящий момент шины
_Tf	Момент трения
_Ti	Чистый входной крутящий момент
_Tk	Кинетический момент трения
_Кому	Чистый выходной крутящий момент
_Ts	Статический фрикционный момент
_ФК	Приложенное усилие сцепления
_Fx	Продольное усилие, создаваемое дорожным покрытием шины из-за проскальзывания
_Reff	Эффективный радиус сцепления
_Ro	Внешний радиус кольцевого диска
_Ri	Внутренний радиус кольцевого диска
_Ре	Эффективный радиус шины при нагрузке и при заданном давлении
_Vx	Скорость продольной оси
_Fz	Нормальная сила транспортного средства
ɑ	Показатель давления в шинах
β	Показатель нормальной силы
_пи	Давление в шинах
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Системы координат шин и колес

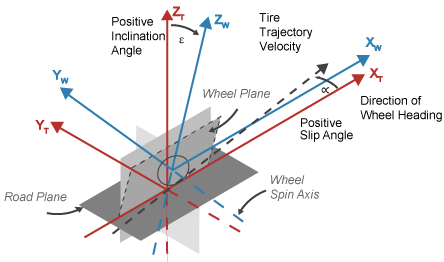
Для разрешения сил и моментов блок использует ориентацию Z-Up систем координат шины и колеса.

Оси системы координат шины (_XT, _YT, _ZT) закреплены в опорной раме, прикрепленной к шине. Начало координат находится в контакте шины с землей.
Оси системы координат колеса (_XW, _YW, _ZW) фиксируются в опорной раме, прикрепленной к колесу. Начало координат находится в центре колеса.

Ориентация Z-Up ^[1 ]

Z-Up tire and wheel coordinate systems showing wheel plane and road plane

Тормоза

Диск

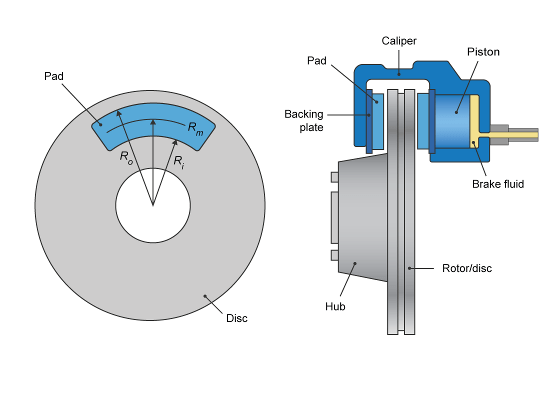
Если задан параметр «Тип тормоза» Discблок реализует дисковый тормоз. На этом рисунке показаны вид сбоку и спереди дискового тормоза.

Front and side view of disc brake, showing pad, disc, and caliper

Дисковый тормоз преобразует давление в тормозном цилиндре в силу. Дисковый тормоз прикладывает усилие к среднему радиусу тормозной колодки.

Блок использует эти уравнения для вычисления тормозного момента дискового тормоза.

$T = \begin{matrix} \frac{{_{}^{}_{}_{}}{} мкPāBa2RmNpads4 при \\ \frac{_{N≠0μstaticPπBa2RmNpads4,}_{}^{когда}_{N}_{= 0}}{} \end{matrix}$

$Rm \frac{= Ro}{+}$ Ri2

Уравнения используют эти переменные.

T	Тормозной момент
P	Приложенное тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в узле дискового тормоза
_μstatic	Коэффициент статического трения дисковой площадки-ротора
μ	Коэффициент кинетического трения дисковой площадки-ротора
_Ba	Диаметр отверстия тормозного привода
_{Комната}	Средний радиус приложения усилия тормозной колодки к тормозному ротору
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если задан параметр «Тип тормоза» Drumблок реализует статический (стационарный) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двустороннего гидропривода и двух тормозных колодок. Тормозные колодки не имеют общего шарнирного пальца.

Симплексная модель барабанного тормоза использует приложенную силу и геометрию тормоза для расчета чистого крутящего момента для каждой тормозной колодки. Модель барабана предполагает, что приводы и геометрия колодки симметричны для обеих сторон, позволяя использовать единый набор параметров геометрии и трения для обеих колодок.

Блок реализует уравнения, полученные из этих уравнений в основах элементов машины.

$\begin{array}{l} _{Trshoe} = \frac{(½ мккр (_{} cosü 2 -_{}_{}^{}}{cosun1) Ba22μ (_{} 2r (_{} cosstart2 -^{}_{cosstart1}) +^{a}_{(} cos2ü 2 -_{}_{} cos2start1)) +_{} ar (_{2start1}} - \\ _{2ü 2 +} \frac{sin2start2 -_{} sin2start1))_{}_{}^{}}{PTlshoe = ({½ мккр}_{} (_{cosü 2} -^{cosun1})_{} {Ba2}^{−}_{} 2λ (2λ (2r (_{}_{}_{}_{}} \end{array}$

$T = \begin{matrix} _{{} {Trshoe}_{+} Tlshoe при N≠0 ( Trshoe + \\ _{Tlshoe)}_{} мкстатически, \frac{_{когда N}}{} = 0 \end{matrix}$

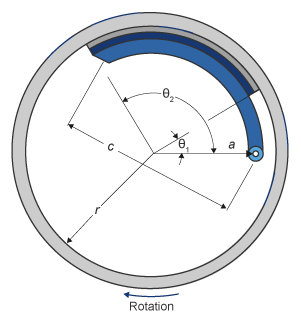
Side view of drum brake

Уравнения используют эти переменные.

T	Тормозной момент
P	Приложенное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент статического трения дисковой площадки-ротора
μ	Коэффициент кинетического трения дисковой площадки-ротора
_Trshoe	Тормозной момент правой колодки
_Tlshoe	Тормозной момент левой колодки
a	Расстояние от центра барабана до центра оси шарнира колодки
c	Расстояние от центра оси шарнира колодки до соединения тормозного привода на тормозной колодке
r	Внутренний радиус барабана
_Ba	Диаметр отверстия тормозного привода
_Θ1	Угол от центра оси шарнира колодки до начала материала тормозной колодки на колодке
_Θ2	Угол от центра оси шарнира колодки до конца материала тормозной колодки на колодке

Нанесенный на карту

Если задан параметр «Тип тормоза» Mappedблок использует таблицу поиска для определения тормозного момента.

$T = \begin{matrix} _{{} fbrake (P, N ) при N≠0 ( мкстатически ) \\ \frac{_{fbrake (P,}}{} N)_{при} N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Тормозной момент
$_{fbreake}^{} (P,$ N)	Таблица поиска тормозного момента
P	Приложенное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения поверхности поверхности контакта барабана в статических условиях
μ	Коэффициент трения поверхности раздела диск-подушка-ротор

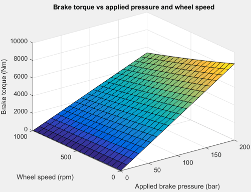
Справочная таблица для тормозного момента, $_{fbreake}^{} (P,$ N), является функцией приложенного тормозного давления и скорости колеса, где:

T - тормозной момент в Н· м.
Р - давление торможения, в бар.
N - частота вращения колеса, в об/мин.

Plot of brake torque as a function of wheel speed and applied brake pressure

Порты

Вход

развернуть все

`BrkPrs` - Тормозное давление
`scalar` | `N`около-`1` вектор

Давление тормозов, в Па.

Вектор - число колес, N, на 1. Если задано скалярное значение, блок предполагает, что число штурвалов равно единице.

Зависимости

Чтобы включить этот порт, для параметра Brake Type укажите один из следующих типов:

Disc
Drum
Mapped

`AxlTrq` - Крутящий момент оси
`scalar` | `N`около-`1` вектор

Крутящий момент оси, _Та, вокруг оси вращения колеса, в Н· м.

`Vx` - Продольная скорость
`scalar` | `N`около-`1` вектор

Продольная скорость оси, _Vx, вдоль оси х, закрепленной на шине, в м/с.

`Vy` - Поперечная скорость
`scalar` | `N`около-`1` вектор

Поперечная скорость оси, _Vy, вдоль оси y, зафиксированной в шине, в м/с.

`Camber` - Угол развала
`scalar` | `N`около-`1` вектор

Угол развала, ɣ, в рад.

`YawRate` - Угловая скорость шины
`scalar` | `N`около-`1` вектор

Угловая скорость шины, r, вокруг фиксированной z-оси шины (скорость рыскания), в рад/с.

`Prs` - Давление накачки шины
`scalar` | `N`около-`1` вектор

Давление накачки шин, _пи, в Па.

`Gnd` - Смещение грунта
`scalar` | `N`около-`1` вектор

Перемещение грунта вдоль оси z, зафиксированной в шине, в м. Положительный ввод обеспечивает подъем колеса.

`Fext` - Усилие на ось, приложенное к шине
`scalar` | `N`около-`1` вектор

Усилие оси, приложенное к шине, _Fxt, вдоль оси z, закрепленной на транспортном средстве (положительный ввод сжимает шину), в Н.

`ScaleFctrs` - Масштабные коэффициенты
`27`около-`N` множество

Массив масштабного коэффициента Magic Formula. Размеры массива: 27 по количеству колёс, Н.

Уравнения магической формулы используют масштабные коэффициенты для учета статических или имитационных изменений времени выполнения. Номинально для большинства установлено значение 1.

Элемент массива	Переменная	Масштабный коэффициент
`ScaleFctrs(1,1)`	`lam_Fzo`	Номинальная нагрузка
`ScaleFctrs(2,1)`	`lam_mux`	Коэффициент трения продольного пика
`ScaleFctrs(3,1)`	`lam_muy`	Коэффициент бокового пикового трения
`ScaleFctrs(4,1)`	`lam_muV`	Скорость скольжения Vs затухающее трение
`ScaleFctrs(5,1)`	`lam_Kxkappa`	Жесткость при проскальзывании тормоза
`ScaleFctrs(6,1)`	`lam_Kyalpha`	Жесткость при повороте
`ScaleFctrs(7,1)`	`lam_Cx`	Коэффициент продольной формы
`ScaleFctrs(8,1)`	`lam_Cy`	Коэффициент поперечной формы
`ScaleFctrs(9,1)`	`lam_Ex`	Коэффициент продольной кривизны
`ScaleFctrs(10,1)`	`lam_Ey`	Коэффициент поперечной кривизны
`ScaleFctrs(11,1)`	`lam_Hx`	Продольное горизонтальное смещение
`ScaleFctrs(12,1)`	`lam_Hy`	Поперечный горизонтальный сдвиг
`ScaleFctrs(13,1)`	`lam_Vx`	Продольное вертикальное смещение
`ScaleFctrs(14,1)`	`lam_Vy`	Поперечный вертикальный сдвиг
`ScaleFctrs(15,1)`	`lam_Kygamma`	Жесткость силы развала
`ScaleFctrs(16,1)`	`lam_Kzgamma`	Жесткость крутящего момента развала
`ScaleFctrs(17,1)`	`lam_t`	Пневматический след (воздействующий на жесткость центрирующего крутящего момента)
`ScaleFctrs(18,1)`	`lam_Mr`	Остаточный крутящий момент
`ScaleFctrs(19,1)`	`lam_xalpha`	Альфа-влияние на Fx (каппа)
`ScaleFctrs(20,1)`	`lam_ykappa`	Влияние Каппы на Fy (альфа)
`ScaleFctrs(21,1)`	`lam_Vykappa`	Наведенный слой руля Fy
`ScaleFctrs(22,1)`	`lam_s`	Мгновенное плечо Fx
`ScaleFctrs(23,1)`	`lam_Cz`	Радиальная жесткость шины
`ScaleFctrs(24,1)`	`lam_Mx`	Жесткость опрокидывающейся пары
`ScaleFctrs(25,1)`	`lam_VMx`	Вертикальный сдвиг опрокидывающей пары
`ScaleFctrs(26,1)`	`lam_My`	Момент сопротивления качению
`ScaleFctrs(27,1)`	`lam_Mphi`	Парковочный момент Mz

Продукция

развернуть все

`Info` - Блочные данные
автобус

Блочные данные, возвращаемые как сигнал шины, содержащий эти блочные значения.

Сигнал	Описание	Единицы
`AxlTrq`	Крутящий момент оси вокруг оси Y, закрепленной на колесе	Н· м
`Omega`	Угловая скорость колеса вокруг фиксированной оси y	рад/с
`Fx`	Продольное усилие транспортного средства вдоль оси Х, закрепленной на шине	N
`Fy`	Боковое усилие транспортного средства вдоль оси Y, закрепленной в шине	N
`Fz`	Вертикальное усилие транспортного средства вдоль оси Z, закрепленной на шине	N
`Mx`	Опрокидывающий момент вокруг закрепленной в шине оси x	Н· м
`My`	Крутящий момент сопротивления качению вокруг оси Y, закрепленной в шине	Н· м
`Mz`	Выравнивающий момент вокруг оси Z, закрепленной в шине	Н· м
`Vx`	Продольная скорость транспортного средства вдоль оси Х, закрепленной на шине	м/с
`Vy`	Поперечная скорость транспортного средства вдоль оси Y, закрепленной на шине	м/с
`Re`	Загруженный эффективный радиус	m
`Kappa`	Коэффициент продольного проскальзывания	НА
`Alpha`	Угол бокового проскальзывания	радиус
`a`	Длина половины контактного сегмента	m
`b`	Контактное поле половинной ширины	m
`Gamma`	Угол развала	радиус
`psidot`	Угловая скорость шины вокруг оси z (скорость рыскания)	рад/с
`BrkTrq`	Тормозной момент вокруг оси Y, закрепленной на транспортном средстве	Н· м
`BrkPrs`	Давление тормоза	Pa
`z`	Вертикальное перемещение оси вдоль оси Z, закрепленной на шине	m
`zdot`	Вертикальная скорость оси вдоль оси Z, закрепленной в шине	м/с
`Gnd`	Перемещение грунта вдоль оси Z, закрепленной в шине (положительный ввод обеспечивает подъем колеса)	m
`GndFz`	Вертикальная сила боковины на земле вдоль оси Z, закрепленной на шине	N
`Prs`	Давление накачки шины	Pa

`Omega` - Угловая скорость колеса
`scalar` | `N`около-`1` вектор

Угловая скорость колеса, λ, вокруг фиксированной колесом оси y, в рад/с.

`Fx` - Усилие продольной оси
`scalar` | `N`около-`1` вектор

Продольная сила, действующая на ось _Fx вдоль оси х, зафиксированной в шине, в N. Положительная сила действует для перемещения транспортного средства вперед.

`Fy` - Сила поперечной оси
`scalar` | `N`около-`1` вектор

Боковая сила, действующая на ось Fy вдоль оси y, зафиксированной в шине, в Н.

`Fz` - Сила вертикальной оси
`scalar` | `N`около-`1` вектор

Вертикальная сила, действующая на ось, _Fz, вдоль неподвижной оси z шины, в Н.

`Mx` - Опрокидывающий момент
`scalar` | `N`около-`1` вектор

Продольный момент, действующий на ось, _Mx, вокруг неподвижной оси х шины, в Н· м.

`My` - Катящийся резистивный момент
`scalar` | `N`около-`1` вектор

Боковой момент, воздействующий на ось, _Му, вокруг зафиксированной в шине оси Y, в Н· м.

`Mz` - Выравнивающий момент
`scalar` | `N`около-`1` вектор

Вертикальный момент, действующий на ось, _Mz, вокруг неподвижной оси z шины, в Н· м.

Параметры

развернуть все

Параметры блока

`Tire Type` - Выберите тип
`External file` (по умолчанию) | `Light passenger car 205/60R15` | `Mid-size passenger car 235/45R18` | `Performance car 225/40R19` | `SUV 265/50R20` | `Light truck 275/65R18` | `Commercial truck 295/75R22.5`

Используйте параметр Тип шины (Tire type) для выбора источника данных шины.

Цель Действие

Цель	Действие
Реализация формулы Magic с использованием эмпирических уравнений ^{[1] и [2}]. В уравнениях используются коэффициенты подгонки, соответствующие параметрам блока.	Обновите параметры блока с помощью коэффициентов фитинга из файла: Задайте для параметра «Тип шины» значение `External file`. На панели «Параметры колеса и шины» > «Шина» выберите «Выбрать файл». Выберите файл коэффициентов шины. Выберите Обновить значения маски из файла. В диалоговом окне с запросом подтверждения нажмите кнопку ОК. Блок обновляет параметры. Выберите «Применить».
Внедрение наборов данных по подогнанным шинам, предоставленных Глобальным центром моделирования производительности автомобилей (GCAPS).	Обновить соответствующие параметры блока с помощью данных о встроенных шинах GCAPS: Задайте тип шины, который требуется реализовать. Варианты включают в себя: `Light passenger car 205/60R15` `Mid-size passenger car 235/45R18` `Performance car 225/40R19` `SUV 265/50R20` `Light truck 275/65R18` `Commercial truck 295/75R22.5` Выберите Обновить применимые параметры шины с помощью значений типа шины. На вкладке «Параметры шины» блок обновляет применимые параметры, включая ширину колеса, радиус обода и массу колеса. Выберите «Применить».

Обновите параметры блока с помощью коэффициентов фитинга из файла:

Задайте для параметра «Тип шины» значение External file.
На панели «Параметры колеса и шины» > «Шина» выберите «Выбрать файл».
Выберите файл коэффициентов шины.
Выберите Обновить значения маски из файла. В диалоговом окне с запросом подтверждения нажмите кнопку ОК. Блок обновляет параметры.
Выберите «Применить».

Обновить соответствующие параметры блока с помощью данных о встроенных шинах GCAPS:

Задайте тип шины, который требуется реализовать. Варианты включают в себя:
- Light passenger car 205/60R15
- Mid-size passenger car 235/45R18
- Performance car 225/40R19
- SUV 265/50R20
- Light truck 275/65R18
- Commercial truck 295/75R22.5
Выберите Обновить применимые параметры шины с помощью значений типа шины. На вкладке «Параметры шины» блок обновляет применимые параметры, включая ширину колеса, радиус обода и массу колеса.
Выберите «Применить».

`Brake Type` - Выберите тип
`None` | `Disc` | `Drum` | `Mapped`

Используйте параметр «Тип тормоза» для выбора тормоза.

Цель	Настройка типа тормоза
Без торможения	`None`
Реализовать тормоз, преобразующий давление тормозного цилиндра в тормозное усилие	`Disc`
Реализовать симплексный барабанный тормоз, преобразующий приложенную силу и геометрию тормоза в чистый тормозной момент	`Drum`
Реализовать таблицу поиска, которая является функцией скорости колеса и приложенного тормозного давления	`Mapped`

Тормоз

`Static friction coefficient, mu_static` - Статическое трение
`.3` (по умолчанию) | `scalar`

Коэффициент статического трения, безразмерный.

Зависимости

Чтобы включить этот параметр, для параметра «Тип тормоза» укажите один из следующих типов:

Disc
Drum
Mapped

`Kinetic friction coefficient, mu_kinetic` - Кинетическое трение
`.2` (по умолчанию) | `scalar`

Коэффициент кинематического трения, безразмерный.

Зависимости

Чтобы включить этот параметр, для параметра «Тип тормоза» укажите один из следующих типов:

Disc
Drum
Mapped

Диск

`Disc brake actuator bore, disc_abore` - Расстояние ствола
`.05` (по умолчанию) | `scalar`

Отверстие привода дискового тормоза, в м.

Зависимости

Для включения параметров дискового тормоза выберите Disc для параметра «Тип тормоза».

`Brake pad mean radius, Rm` - Радиус
`.177` (по умолчанию) | `scalar`

Средний радиус тормозной колодки, в м.

Зависимости

Для включения параметров дискового тормоза выберите Disc для параметра «Тип тормоза».

`Number of brake pads, num_pads` - Подсчет
`2` (по умолчанию) | `scalar`

Количество тормозных колодок.

Зависимости

Для включения параметров дискового тормоза выберите Disc для параметра «Тип тормоза».

Барабан