Геометрическая калибровка камеры, также называемая повторным резектированием камеры, оценивает параметры объектива и датчика изображения изображения или видеокамеры. Эти параметры можно использовать для коррекции искажения объектива, измерения размера объекта в мировых единицах измерения или определения местоположения камеры в сцене. Эти задачи используются в таких приложениях, как машинное зрение для обнаружения и измерения объектов. Они также используются в робототехнике, для навигационных систем, 3-D реконструкции сцен.
Примеры того, что можно сделать после калибровки камеры:

Параметры камеры включают собственные характеристики, внешние характеристики и коэффициенты искажения. Для оценки параметров камеры необходимо иметь 3-D точки мира и соответствующие им точки изображения 2-D. Эти соответствия можно получить с помощью нескольких изображений шаблона калибровки, например шахматной доски. С помощью соответствий можно определить параметры камеры. После калибровки камеры для оценки точности расчетных параметров можно:
Постройте график относительного расположения камеры и шаблона калибровки
Вычислите ошибки повторного впрыска.
Вычислите ошибки оценки параметров.
С помощью калибратора камеры можно выполнить калибровку камеры и оценить точность расчетных параметров.
Компьютерное зрение Toolbox™ содержит алгоритмы калибровки для модели камеры с микроотверстием и модели камеры с рыбьим глазом. Можно использовать модель рыбьего глаза с камерами до поля зрения (ФОВ) 195 градусов.
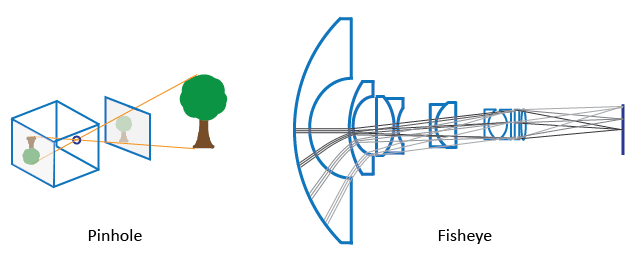
Алгоритм калибровки микроотверстий основан на модели, предложенной Жаном-Ивом Буге [3]. Модель включает в себя модель камеры с микроотверстием [1] и искажение объектива [2]. Модель камеры с микроотверстием не учитывает искажение объектива, поскольку идеальная камера с микроотверстием не имеет объектива. Для точного представления реальной камеры модель полной камеры, используемая алгоритмом, включает радиальное и тангенциальное искажения объектива.
Из-за экстремального искажения, создаваемого линзой рыбьего глаза, модель микроотверстия не может моделировать камеру рыбьего глаза. Дополнительные сведения о калибровке камеры с использованием модели fisheye см. в разделе Основы калибровки Fisheye.
Микроотверстная камера - простая камера без объектива и с единственной малой апертурой. Световые лучи проходят через апертуру и проецируют перевернутое изображение на противоположную сторону камеры. Считайте, что виртуальная плоскость изображения находится перед камерой и содержит вертикальное изображение сцены.
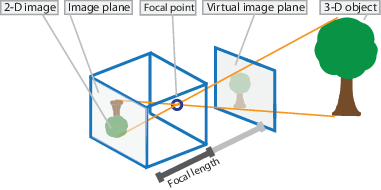
Параметры фотоаппарата представлены в матрице 4 на 3, называемой матрицей фотоаппарата. Эта матрица отображает 3-D мировую сцену в плоскость изображения. Алгоритм калибровки вычисляет матрицу камеры с использованием внешних и внутренних параметров. Внешние параметры представляют расположение камеры в сцене 3-D. Внутренние параметры представляют оптический центр и фокусное расстояние камеры.
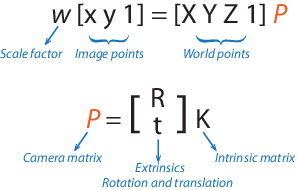
Точки мира преобразуются в координаты камеры с использованием параметров внешней среды. Координаты камеры отображаются в плоскости изображения с использованием собственных параметров.
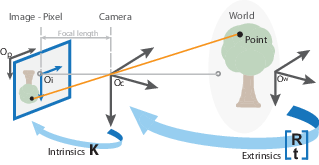
Алгоритм калибровки вычисляет матрицу камеры с использованием внешних и внутренних параметров. Внешние параметры представляют собой жесткое преобразование мировой системы координат 3-D систему координат 3-D камеры. Внутренние параметры представляют собой проективное преобразование из координат 3-D камеры в координаты 2-D изображения.
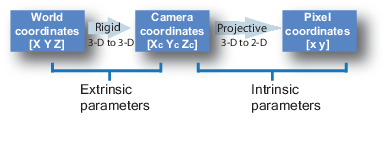
Внешние параметры состоят из поворота, R и перемещения, т. Начало системы координат камеры находится в ее оптическом центре, а ее оси x и y определяют плоскость изображения.

Внутренние параметры включают фокусное расстояние, оптический центр, также известный как главная точка, и коэффициент перекоса. Внутренняя матрица камеры K определяется как:
Перекос пикселя определяется следующим образом:
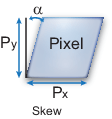
| - оптический центр (главная точка), в пикселях. |
| ) - Фокусное расстояние в пикселях . F/px F/py - фокусное расстояние в мировых единицах, обычно выраженное в миллиметрах. ) - размер пикселя в мировых единицах. |
| - коэффициент перекоса, ненулевой, если оси изображения не перпендикулярны. fxtanα |
Матрица камеры не учитывает искажение объектива, поскольку идеальная камера с микроотверстием не имеет объектива. Для точного представления реальной камеры модель камеры включает радиальное и тангенциальное искажения объектива.
Радиальные искажения возникают, когда лучи света изгибаются больше вблизи краев линзы, чем в ее оптическом центре. Чем меньше линза, тем больше искажение.

Коэффициенты радиального искажения моделируют этот тип искажения. Искаженные точки обозначаются как (xdistorted, ydistorted):
xdistorted = x (1 + k1 * r2 + k2 * r4 + k3 * r6)
ydistorted = y (1 + k1 * r2 + k2 * r4 + k3 * r6)
x, y - неискаженные расположения пикселей. x и y находятся в нормализованных координатах изображения. Нормализованные координаты изображения вычисляют по координатам пикселей путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом, x и y безразмерны.
k1, k2 и k3 - коэффициенты радиального искажения объектива.
r2: x2 + y2
Обычно для калибровки достаточно двух коэффициентов. Для сильного искажения, например в широкоугольных линзах, можно выбрать 3 коэффициента для включения k3.
Касательное искажение происходит, когда объектив и плоскость изображения не параллельны. Коэффициенты тангенциального искажения моделируют этот тип искажения.
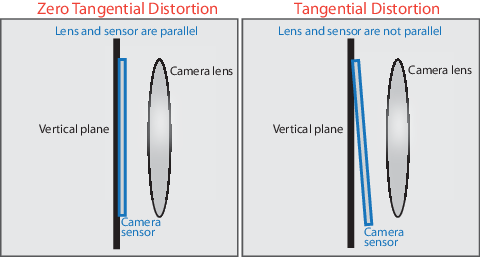
Искаженные точки обозначаются как (xdistorted, ydistorted):
xdistorted = x + [2 * p1 * x * y + p2 * (r2 + 2 * x2)]
ydistorted = y + [p1 * (r2 + 2 * y2) + 2 * p2 * x * y]
x, y - неискаженные расположения пикселей. x и y находятся в нормализованных координатах изображения. Нормализованные координаты изображения вычисляют по координатам пикселей путем перевода в оптический центр и деления на фокусное расстояние в пикселях. Таким образом, x и y безразмерны.
p1 и p2 - коэффициенты тангенциального искажения линзы.
r2: x2 + y2
[1] Чжан, З. «Новый гибкий метод калибровки камеры». Транзакции IEEE по анализу шаблонов и машинному интеллекту. т. 22, № 11, 2000, с. 1330-1334.
[2] Хейккила, Дж., и О. Сильвен. «Четырехэтапная процедура калибровки камеры с неявной коррекцией изображения». Международная конференция IEEE по компьютерному зрению и Recognition.1997 шаблонов.
[3] Буге, J. Y. «Панель инструментов калибровки камеры для Matlab». Вычислительное видение в Калифорнийском технологическом институте. Панель инструментов калибровки камеры для MATLAB
[4] Брэдски, Г. и А. Келер. Обучение OpenCV: компьютерное видение с помощью библиотеки OpenCV. Себастополь, Калифорния: О'Райлли, 2008.