Вычисление вейвлет-коэффициентов при каждом возможном масштабе - это изрядный объем работы, и он генерирует ужасное количество данных. Что, если мы выберем только подмножество шкал и позиций, на которых мы будем делать наши расчеты?
Оказывается, довольно примечательно, что если мы выберем шкалы и позиции, основанные на степенях двух - так называемых диадических шкал и позиций, - то наш анализ будет гораздо более эффективным и столь же точным. Мы получаем такой анализ из дискретного вейвлет-преобразования (DWT). Дополнительные сведения о DWT см. в разделе Алгоритмы в руководстве пользователя Wavelet Toolbox.
Эффективный способ реализации этой схемы с использованием фильтров был разработан в 1988 году Маллатом (см. [Mal89] в Справочнике). Алгоритм Маллата фактически является классической схемой, известной в сообществе обработки сигналов как двухканальный поддиапазонный кодер (см. стр. 1 книги Wavelets and Filter Banks, by Strang and Nguyen [StrN96]).
Этот очень практичный алгоритм фильтрации дает быстрое вейвлет-преобразование - коробку, в которую проходит сигнал, и из которой быстро выходят вейвлет-коэффициенты. Давайте рассмотрим это более подробно.
Для многих сигналов низкочастотное содержание является наиболее важной частью. Высокочастотное содержание, с другой стороны, придает вкус или нюанс. Рассмотрим человеческий голос. Если удалить высокочастотные компоненты, голос звучит по-другому, но вы все равно можете сказать, что говорят. Однако, если удалить достаточно низкочастотных компонентов, вы услышите гиббериш.
В вейвлет-анализе мы часто говорим о приближениях и деталях. Аппроксимации являются высокомасштабными низкочастотными составляющими сигнала. Детали - низкомасштабные высокочастотные компоненты.
Процесс фильтрации на самом базовом уровне выглядит следующим образом.
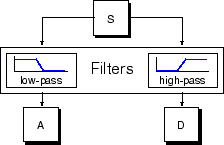
Исходный сигнал, S, проходит через два комплементарных фильтра и выходит в виде двух сигналов.
К сожалению, если мы действительно выполняем эту операцию над реальным цифровым сигналом, мы получаем вдвое больше данных, чем начали с. Предположим, например, что исходный сигнал S состоит из 1000 выборок данных. Затем результирующие сигналы будут иметь по 1000 выборок, в общей сложности 2000.
Эти сигналы A и D интересны, но мы получаем 2000 значений вместо 1000, которые у нас были. Существует более тонкий способ выполнения разложения с использованием вейвлетов. Внимательно глядя на вычисления, мы можем сохранить только одну точку из двух в каждой из двух выборок длиной 2000, чтобы получить полную информацию. Это понятие понижающей дискретизации. Мы производим две последовательности, называемые cA и cD.
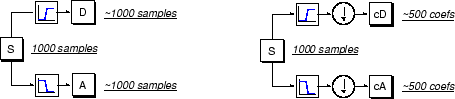
Процесс справа, который включает понижающую выборку, создает коэффициенты DWT.
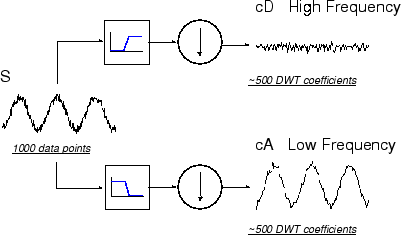
Чтобы лучше понять этот процесс, давайте выполним одноступенчатое дискретное вейвлет-преобразование сигнала. Наш сигнал будет чистой синусоидой с добавленным высокочастотным шумом.
Вот наша принципиальная схема с реальными сигналами, вставленными в нее.
Код MATLAB ®, необходимый для созданияs, cD, и cA является
s = sin(20.*linspace(0,pi,1000)) + 0.5.*rand(1,1000); [cA,cD] = dwt(s,'db2');
где db2 является именем вейвлета, который мы хотим использовать для анализа.
Обратите внимание, что коэффициенты детализации cD малы и состоят в основном из высокочастотного шума, в то время как коэффициенты аппроксимации cA содержат гораздо меньше шума, чем исходный сигнал.
[length(cA) length(cD)] ans = 501 501
Можно заметить, что фактические длины векторов коэффициентов детализации и аппроксимации немного больше половины длины исходного сигнала. Это связано с процессом фильтрации, который реализуется путем свертки сигнала с фильтром. Сверток «размазывает» сигнал, вводя в результат несколько лишних выборок.
Процесс разложения может быть повторен, с последовательными приближениями, разложенными поочередно, так что один сигнал разбивается на множество компонентов с более низким разрешением. Это называется деревом вейвлет-декомпозиции.
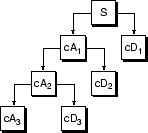
Просмотр дерева вейвлет-разложения сигнала может дать ценную информацию.
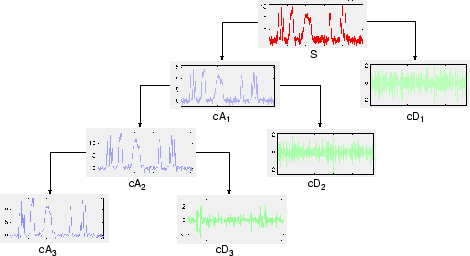
Поскольку процесс анализа итеративен, теоретически он может продолжаться бесконечно. В действительности разложение может продолжаться только до тех пор, пока отдельные детали не будут состоять из одного образца или пикселя. На практике можно выбрать подходящее количество уровней на основе характера сигнала или подходящего критерия, такого как энтропия (см. раздел Выбор оптимальной декомпозиции в руководстве пользователя Wavelet Toolbox).