Способ вейвлет-пакета представляет собой обобщение вейвлет-разложения, которое предлагает более богатый анализ сигнала.
Атомы вейвлет-пакетов индексируются тремя естественно интерпретируемыми параметрами: положением, масштабом (как при вейвлет-разложении) и частотой.
Для данной ортогональной вейвлет-функции мы генерируем библиотеку баз, называемых вейвлет-пакетами баз. Каждая из этих баз предлагает определенный способ кодирования сигналов, сохранения глобальной энергии и восстановления точных признаков. Вейвлет-пакеты могут использоваться для многочисленных расширений данного сигнала. Затем мы выбираем наиболее подходящее разложение данного сигнала относительно критерия, основанного на энтропии.
Существуют простые и эффективные алгоритмы как для вейвлет-разложения пакетов, так и для оптимального выбора декомпозиции. Затем мы можем создать адаптивные алгоритмы фильтрации с непосредственными приложениями для оптимального кодирования сигналов и сжатия данных.
В процедуре ортогональной вейвлет-декомпозиции общий этап разбивает коэффициенты аппроксимации на две части. После разделения получаем вектор коэффициентов аппроксимации и вектор коэффициентов детализации, оба в более грубом масштабе. Информация, потерянная между двумя последовательными приближениями, фиксируется в коэффициентах детализации. Затем следующий этап состоит из разделения нового вектора аппроксимационного коэффициента; последовательные детали никогда не анализируются повторно.
В соответствующей ситуации с вейвлет-пакетом каждый вектор коэффициента детализации также разлагается на две части с использованием того же подхода, что и при разделении вектора аппроксимации. Это предлагает самый богатый анализ: создается полное двоичное дерево, как показано на следующем рисунке.
Дерево декомпозиции вейвлет-пакетов на уровне 3
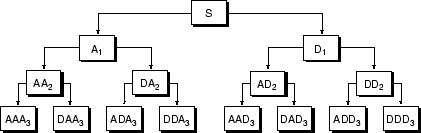
Идея этого разложения состоит в том, чтобы начать с масштабно-ориентированного разложения, а затем проанализировать полученные сигналы на частотных поддиапазонах.
Следующие простые примеры иллюстрируют некоторые различия между вейвлет-анализом и вейвлет-анализом пакетов.
Спектральный анализ широкополосных стационарных сигналов с использованием преобразования Фурье хорошо зарекомендовал себя. Для нестационарных сигналов существуют локальные методы Фурье, такие как кратковременное преобразование Фурье (STFT). Краткое описание см. в разделе Короткое преобразование Фурье.
Поскольку вейвлеты локализованы во времени и частоте, можно использовать аналоги на основе вейвлетов к STFT для частотно-временного анализа нестационарных сигналов. Например, можно построить скалограмму (wscalogram) на основе непрерывного вейвлет-преобразования (CWT). Однако потенциальный недостаток использования CWT заключается в том, что он является дорогостоящим в вычислительном отношении.
Дискретное вейвлет-преобразование (DWT) допускает частотно-временное разложение входного сигнала, но степень разрешения частоты в DWT обычно считается слишком грубой для практического частотно-временного анализа.
В качестве компромисса между методами на основе DWT- и CWT вейвлет-пакеты обеспечивают вычислительно эффективную альтернативу с достаточным частотным разрешением. Вы можете использовать wpspectrum для выполнения частотно-временного анализа сигнала с использованием вейвлет-пакетов.
Следующие примеры иллюстрируют использование вейвлет-пакетов для выполнения локального спектрального анализа. В следующих примерах также используется spectrogram (Signal Processing Toolbox) из программного обеспечения Signal Processing Toolbox™ в качестве эталона для сравнения со спектром вейвлет-пакетов. Если у вас нет программного обеспечения Signal Processing Toolbox, вы можете просто запустить примеры спектра вейвлет-пакетов.
Вейвлет-пакетный спектр синусоидальной волны.
fs = 1000; % sampling rate t = 0:1/fs:2; % 2 secs at 1kHz sample rate y = sin(256*pi*t); % sine of period 128 level = 6; wpt = wpdec(y,level,'sym8'); [Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');
При наличии программного обеспечения Signal Processing Toolbox можно вычислить кратковременное преобразование Фурье.
figure; windowsize = 128; window = hanning(windowsize); nfft = windowsize; noverlap = windowsize-1; [S,F,T] = spectrogram(y,window,noverlap,nfft,fs); imagesc(T,F,log10(abs(S))) set(gca,'YDir','Normal') xlabel('Time (secs)') ylabel('Freq (Hz)') title('Short-time Fourier Transform spectrum')
Сумма двух синусоидальных волн с частотами 64 и 128 герц.
fs = 1000; t = 0:1/fs:2; y = sin(128*pi*t) + sin(256*pi*t); % sine of periods 64 and 128. level = 6; wpt = wpdec(y,level,'sym8'); [Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');
При наличии программного обеспечения Signal Processing Toolbox можно вычислить кратковременное преобразование Фурье.
figure; windowsize = 128; window = hanning(windowsize); nfft = windowsize; noverlap = windowsize-1; [S,F,T] = spectrogram(y,window,noverlap,nfft,fs); imagesc(T,F,log10(abs(S))) set(gca,'YDir','Normal') xlabel('Time (secs)') ylabel('Freq (Hz)') title('Short-time Fourier Transform spectrum')
Сигнал с резким изменением частоты от 16 до 64 герц через две секунды.
fs = 500; t = 0:1/fs:4; y = sin(32*pi*t).*(t<2) + sin(128*pi*t).*(t>=2); level = 6; wpt = wpdec(y,level,'sym8'); [Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');
При наличии программного обеспечения Signal Processing Toolbox можно вычислить кратковременное преобразование Фурье.
figure; windowsize = 128; window = hanning(windowsize); nfft = windowsize; noverlap = windowsize-1; [S,F,T] = spectrogram(y,window,noverlap,nfft,fs); imagesc(T,F,log10(abs(S))) set(gca,'YDir','Normal') xlabel('Time (secs)') ylabel('Freq (Hz)') title('Short-time Fourier Transform spectrum')
Вейвлет-пакетный спектр линейного чирпа.
fs = 1000; t = 0:1/fs:2; y = sin(256*pi*t.^2); level = 6; wpt = wpdec(y,level,'sym8'); [Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');
При наличии программного обеспечения Signal Processing Toolbox можно вычислить кратковременное преобразование Фурье.
figure; windowsize = 128; window = hanning(windowsize); nfft = windowsize; noverlap = windowsize-1; [S,F,T] = spectrogram(y,window,noverlap,nfft,fs); imagesc(T,F,log10(abs(S))) set(gca,'YDir','Normal') xlabel('Time (secs)') ylabel('Freq (Hz)') title('Short-time Fourier Transform spectrum')
Вейвлет-пакетный спектр квадратичной чирпы.
y = wnoise('quadchirp',10); len = length(y); t = linspace(0,5,len); fs = 1/t(2); level = 6; wpt = wpdec(y,level,'sym8'); [Spec,Time,Freq] = wpspectrum(wpt,fs,'plot');
При наличии программного обеспечения Signal Processing Toolbox можно вычислить кратковременное преобразование Фурье.
windowsize = 128; window = hanning(windowsize); nfft = windowsize; noverlap = windowsize-1; imagesc(T,F,log10(abs(S))) set(gca,'YDir','Normal') xlabel('Time (secs)') ylabel('Freq (Hz)') title('Short-time Fourier Transform spectrum')
Схема вычисления для генерации вейвлет-пакетов проста при использовании ортогонального вейвлета. Начнем с двух фильтров длины 2N, где h(n) и g(n), соответствуют вейвлету.
Теперь по индукции определим следующую последовательность функций:
(Wn (x), n = 0, 1, 2,...)
около
2x − k)
(2x − k)
где W0(x) = φ(x) является функцией масштабирования и W1(x) = ψ(x) - вейвлет-функция.
Например, для вейвлета Хаара, который у нас есть
(1) = 12
и
1) = 12
Уравнения становятся
(2x − 1)
и
Wn (2x − 1)
W0(x) = φ(x) является функцией масштабирования Хаара и W1(x) = ψ(x) является вейвлетом Хаара, поддерживаемым в [0, 1]. Затем мы можем получить W2n путем добавления двух 1/2 масштабированных версий Wn с различными опорами [0,1/2] и [1/2,1] и получить W2n + 1 путем вычитания тех же версий Wn.
Для n = от 0 до 7 мы имеем W-функции, показанные на рисунке Пакеты вейвлета Haar.
Пакеты Wavelet Haar
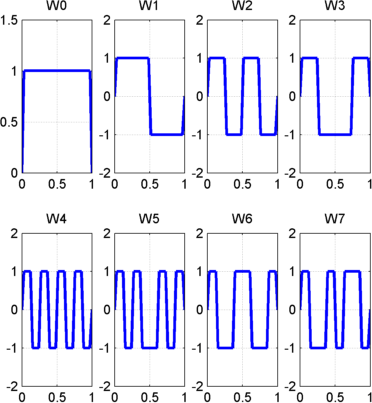
Это можно получить с помощью следующей команды:
[wfun,xgrid] = wpfun('db1',7,5);
который возвращается в wfun приблизительные значения Wn для n = от 0 до 7, вычисленные на 1/25 сетке опоры xgrid.
Начиная с более регулярных оригинальных вейвлетов и используя аналогичную конструкцию, получаем сглаженные версии этой системы W-функций, все с поддержкой в интервале [0, 2N-1]. На рисунке db2 Vavelet Packets представлена система W-функций для исходного db2 вейвлет.
db2 Вейвлет-пакеты
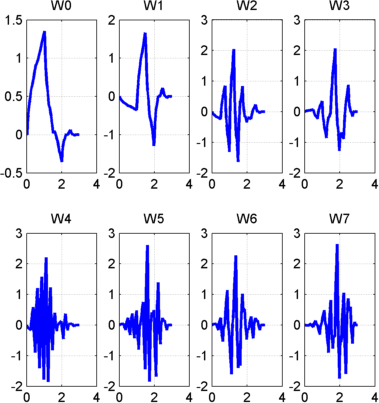
Начиная с функций n∈N) и следуя той же строке, ведущей к ортогональным вейвлетам, рассмотрим трёхиндексное семейство анализирующих функций (формы волн):
(2 − jx − k)
где n∊N и (j, k) ∊Z2.
Как и в вейвлет-фреймворке, k можно интерпретировать как параметр локализации времени, а j как параметр масштаба. Так какова интерпретация n?
Основная идея вейвлет-пакетов состоит в том, что для фиксированных значений j и k Wj, n, k анализирует флуктуации сигнала приблизительно вокруг положения 2j· k, на шкале 2j и на различных частотах для различных допустимых значений последнего параметра n.
На самом деле, тщательно исследуя вейвлет-пакеты, отображаемые в пакетах вейвлета Haar и пакетах вейвлета db2, естественно упорядоченный Wn для n = 0, 1,..., 7, не совпадает точно с порядком, определенным числом колебаний. Точнее, подсчет количества нулевых переходов (пересечений вверх и вниз) для db1 вейвлет-пакеты, у нас есть следующее.
Так, для восстановления свойства, что основная частота увеличивается монотонно с порядком, удобно определить порядок частот, полученный из естественного рекурсивно.
Как видно на предыдущих чертежах, Wr (n)(x) «колеблется» приблизительно n раз.
Для анализа сигнала (например, чирпа из примера 2) лучше построить график коэффициентов вейвлет-пакета, следующих за порядком частот, от низких частот в нижней части до высоких частот в верхней части, а не естественно упорядоченных коэффициентов.
При построении графиков коэффициентов различные опции, связанные с выбором порядка «Частота» или «Естественный», доступны с помощью приложения Wavelet Analyzer.
Эти параметры также доступны в режиме командной строки при использовании wpviewcf функция.
Набор функций Wj, n =(Wj,n,k(x),k∊Z) является (j, n) вейвлет-пакетом. Для положительных значений целых чисел j и n вейвлет-пакеты организованы в деревьях. Дерево на рисунке Vavelet Packets Organized in a Tree; Масштаб j Определяет глубину и частоту n Определяет положение в дереве, чтобы получить максимальное разложение уровня, равное 3. Для каждой шкалы j возможные значения параметра n равны 0, 1,..., 2j-1.
Вейвлет-пакеты, организованные в дереве; Масштаб j Определяет глубину и частоту n Определяет положение в дереве
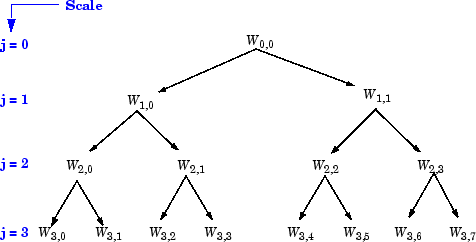
Обозначение Wj, n, где j обозначает параметр масштаба и n параметр частоты, согласуется с обычной маркировкой дерева положения глубины.
У нас , k∈Z) и − k), k∈Z).
Оказывается, что библиотека баз вейвлет-пакетов содержит базис вейвлета, а также несколько других баз. Давайте посмотрим на некоторые из этих баз. Точнее, пусть V0 обозначает пространство (охватываемое W0,0 семейства), в котором лежит анализируемый сигнал; затем (Wd,1; d ≥ 1) - ортогональный базис V0.
Для каждого строго положительного целого числа D, (WD,0, (Wd,1; 1 ≤ d ≤ D)) - ортогональный базис V0.
Известно также, что семейство функций {(Wj + 1, 2n), (Wj + 1, 2n + 1)} является ортогональным базисом пространства, охватываемого Wj, n, которое разделено на два подпространства: Wj + 1, 2n охватывает первое подпространство, и Wj + 1, 2n + 1 второе.
Это последнее свойство дает точную интерпретацию разделения в дереве организации вейвлет-пакетов, поскольку все развитые узлы имеют вид, показанный на рисунке Дерево вейвлет-пакетов: разделение и слияние.
Отсюда следует, что листья каждого связного двоичного поддерева полного дерева соответствуют ортогональной основе начального пространства.
Для сигнала с конечной энергией, принадлежащего V0, любой вейвлет-пакетный базис обеспечит точную реконструкцию и предложит конкретный способ кодирования сигнала, используя распределение информации в поддиапазонах частотной шкалы.
На основе организации библиотеки вейвлет-пакетов естественно подсчитывать разложения, выданные из данного ортогонального вейвлета.
Сигнал длиной N = 2L может быть расширен α различными способами, где α - число двоичных поддеревьев полного двоичного дерева глубины L. В результате (см. [Mal98] стр. 323).
Поскольку это число может быть очень большим и поскольку явное перечисление обычно неуправляемо, интересно найти оптимальное разложение по отношению к удобному критерию, вычисляемому эффективным алгоритмом. Мы ищем минимум критерия.
Функции проверки свойства типа аддитивности хорошо подходят для эффективного поиска структур двоичного дерева и фундаментального разделения. Классические критерии, основанные на энтропии, соответствуют этим условиям и описывают связанные с информацией свойства для точного представления данного сигнала. Энтропия - распространённое понятие во многих областях, главным образом в обработке сигналов. Приведем четыре различных критерия энтропии (см. [CoiW92]); многие другие доступны и могут быть легко интегрированы (тип help wentropy). В следующих выражениях s - сигнал и (si) - коэффициенты s в ортонормированном базисе.
Энтропия E должна быть функцией аддитивной стоимости, так что E (0) = 0 и
si)
Энтропия Шеннона (ненормализованная)
(si2)
так
si2)
с условным обозначением 0log (0) = 0.
Концентрация в лп норма с 1 ℜ ≤ р
si 'p
так
=∑i'si'p=|s'pp
Логарифм энтропии «энергия»
si2)
так
si2)
с журналом соглашений (0) = 0.
Пороговая энтропия
=1>ε и 0 в другом месте, таким образом, E4 (s) = # {я таким образом|>ε} является числом моментов времени, когда сигнал больше, чем порог ε.
Эти функции энтропии доступны с помощью wentropy файл.
Генерируйте сигнал с энергией, равной 1.
s = ones(1,16)*0.25;
Вычислите энтропию Шеннона s.
e1 = wentropy(s,'shannon')
e1 = 2.7726
Вычислите l1.5 энтропию s, эквивалентную norm(s,1.5)1.5.
e2 = wentropy(s,'norm',1.5)
e2 = 2
Вычислите «логарифмическую энергию» энтропии s.
e3 = wentropy(s,'log energy')
e3 = -44.3614
Вычислите пороговую энтропию s, используя пороговое значение 0,24.
e4 = wentropy(s,'threshold', 0.24)
e4 = 16
Этот простой пример иллюстрирует использование энтропии для определения того, представляет ли интерес новое расщепление для получения декомпозиции с минимальной энтропией.
Мы начинаем с постоянного исходного сигнала. Двух частей информации достаточно для определения и восстановления сигнала (т.е. длины и постоянного значения).
w00 = ones(1,16)*0.25;
Вычислить энтропию исходного сигнала.
e00 = wentropy(w00,'shannon')
e00 = 2.7726
Затем разделить w00 использование вейвлета haar.
[w10,w11] = dwt(w00,'db1');
Вычислить энтропию аппроксимации на уровне 1.
e10 = wentropy(w10,'shannon')
e10 = 2.0794
Сведения об уровне 1, w11, равно нулю; энтропия e11 равно нулю. Благодаря свойству аддитивности энтропия разложения задается e10+e11=2.0794. Это должно сравниваться с начальной энтропией e00=2.7726. У нас есть e10 + e11 < e00так что расщепление интересно.
Теперь разделение w10 (не w11 поскольку разделение нулевого вектора не представляет интереса, поскольку энтропия равна нулю).
[w20,w21] = dwt(w10,'db1');
У нас есть w20=0.5*ones(1,4) и w21 равно нулю. Энтропия уровня приближения 2 равна
e20 = wentropy(w20,'shannon')
e20 = 1.3863
Снова у нас есть e20 + 0 < e10Таким образом, расщепление приводит к уменьшению энтропии.
Тогда
[w30,w31] = dwt(w20,'db1');
e30 = wentropy(w30,'shannon')
e30 = 0.6931
[w40,w41] = dwt(w30,'db1')
w40 = 1.0000
w41 = 0
e40 = wentropy(w40,'shannon')
e40 = 0
В последней операции разделения мы обнаруживаем, что только одна часть информации необходима для восстановления исходного сигнала. Вейвлет базис на уровне 4 является лучшим базисом по энтропии Шеннона (с нулевой оптимальной энтропией с e40+e41+e31+e21+e11 = 0).
Выполните разложение вейвлет-пакетов сигнала s, определенного в примере 1.
t = wpdec(s,4,'haar','shannon');
Дерево вейвлет-пакетов в значениях энтропии показывает узлы, помеченные исходными числами энтропии.
Значения энтропии
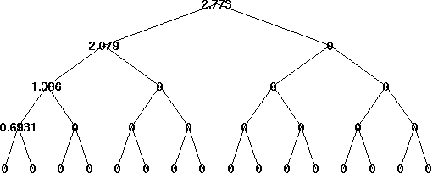
Вычислите лучшее дерево.
bt = besttree(t);
Лучшее дерево показано на следующем рисунке. В этом случае лучшее дерево соответствует вейвлет-дереву. Узлы помечены оптимальной энтропией.
Оптимальные значения энтропии
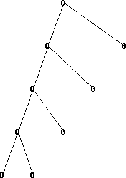
Для использования вейвлет-пакетов требуются связанные с деревом действия и метки. Реализация пользовательского интерфейса строится на этом соображении. Дополнительные сведения о технических деталях см. на справочных страницах.
Полное двоичное дерево глубины D, соответствующее дереву разложения вейвлет-пакетов, разработанному на уровне D, обозначается WPT.
У нас есть следующие интересные поддеревы.
Дерево разложения | Поддерево, такое, что набор листьев является основой |
|---|---|
Дерево разложения вейвлет-пакетов | Полное двоичное дерево: WPT глубины D |
Дерево оптимальной декомпозиции вейвлет-пакетов | Двоичное поддерево WPT |
Дерево наилучшего уровня вейвлет-пакетов | Полное двоичное поддерево WPT |
Дерево вейвлет-декомпозиции | Левое одностороннее двоичное поддерево WPT глубины D |
Дерево наилучшего базиса вейвлета | Левое одностороннее двоичное поддерево WPT |
Выведем следующие определения оптимальных разложений, относительно критерия энтропии Е.
Разложения | Оптимальное разложение | |
|---|---|---|
Вейвлет-разложение пакетов | Поиск по деревьям 2D | Поиск среди D-деревьев |
Вейвлет-разложения | Поиск среди D-деревьев | Поиск среди D-деревьев |
Для любого нетерминального узла мы используем следующий базовый шаг, чтобы найти оптимальное поддерево относительно данного критерия энтропии E (где Eopt обозначает оптимальное значение энтропии).
Условие энтропии | Действие над деревом и маркировкой энтропии |
|---|---|
(c) | Если (node≠root), объединить и задать Eopt (узел) = E (узел) |
| (c) | Разделить и задать (c) |
с естественным исходным условием на ссылочном дереве, Eopt(t) = E(t) для каждого терминального узла t.
Можно использовать функцию wprcoef для восстановления аппроксимации сигнала от любого узла в дереве вейвлет-пакетов. Это справедливо независимо от того, работаете ли вы с полным деревом вейвлет-пакетов или с поддеревом, определяемым критерием оптимальности. Использовать wpcoef если вы хотите извлечь коэффициенты вейвлет-пакета из узла без восстановления аппроксимации к сигналу.
Загрузите шумный доплеровский сигнал.
load noisdopp
Вычислите разложение вейвлет-пакета до уровня 5 с помощью sym4 вейвлет. Используйте режим периодизации.
dwtmode('per');
T = wpdec(noisdopp,5,'sym4');
plot(T)Постройте график двоичного вейвлет-дерева пакетов и щелкните по (4,1) дублету (узел 16).
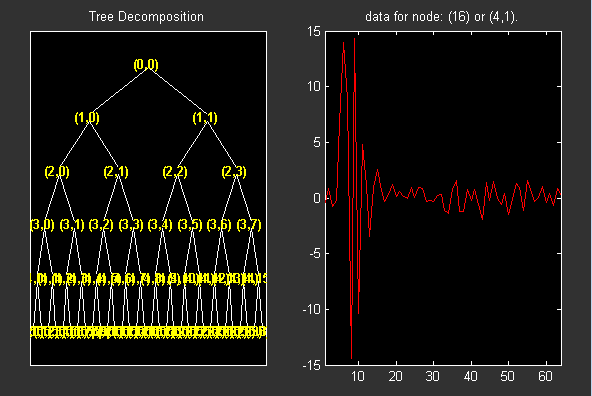
Извлекают коэффициенты вейвлет-пакета из узла 16.
wpc = wpcoef(T,16); % wpc is length 64
Получить приближение к сигналу от узла 16.
rwpc = wprcoef(T,16); % rwpc is length 1024 plot(noisdopp,'k'); hold on; plot(rwpc,'b','linewidth',2); axis tight;
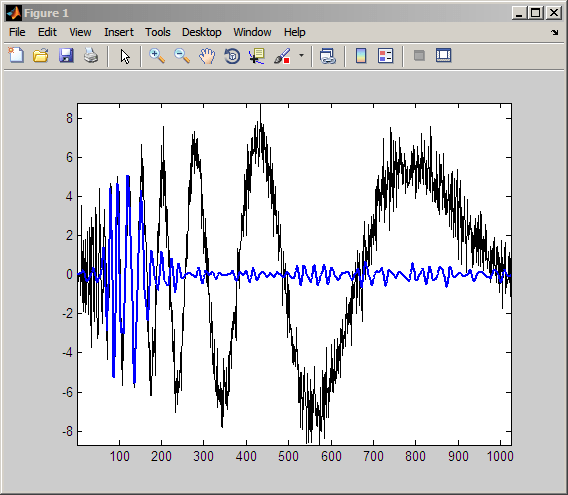
Определите оптимальное дерево двоичных вейвлет-пакетов.
Topt = besttree(T); % plot the best tree plot(Topt)
Реконструируйте приближение к сигналу из (3,0) дублета (узел 7).
rsig = wprcoef(Topt,7); % rsig is length 1024 plot(noisdopp,'k'); hold on; plot(rsig,'b','linewidth',2); axis tight;
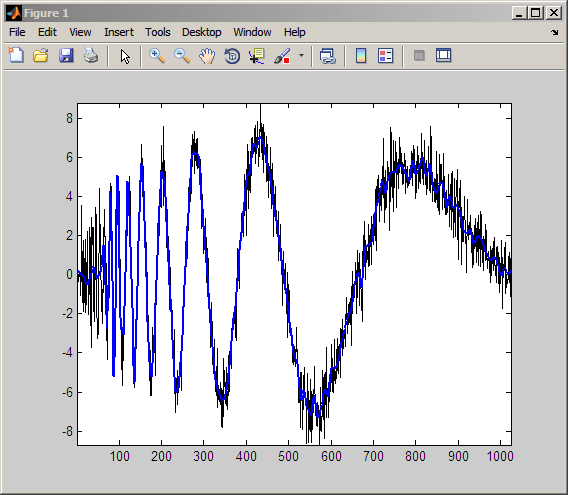
Если известно, какой двойной пакет в двоичном дереве пакетов вейвлет требуется извлечь, можно определить узел, соответствующий этому двойному пакету, с помощью depo2ind.
Например, чтобы определить узел, соответствующий дублету (3,0), введите:
Node = depo2ind(2,[3 0]);
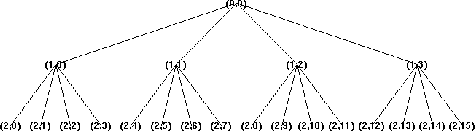
Точно так же, как в случае вейвлет-разложения, предыдущая структура 1-D может быть расширена для анализа изображения. Незначительные прямые изменения приводят к определениям, связанным с четвертичным деревом. На следующем рисунке показан пример глубины 2.
Четвертичное дерево глубины 2
В структуре вейвлет-пакетов идея сжатия и деноизирования идентична идеям, разработанным в структуре вейвлет. Единственной новой функцией является более полный анализ, который обеспечивает повышенную гибкость. Одно разложение с использованием вейвлет-пакетов генерирует большое количество оснований. Затем можно найти наилучшее представление относительно цели конструирования, используя besttree с функцией энтропии.