Алгоритм быстрого вейвлет-преобразования (FWT)

В 1988 году Маллат создал алгоритм быстрого вейвлет-разложения и реконструкции [1]. Алгоритм Маллата для дискретного вейвлет-преобразования (DWT) фактически является классической схемой в сообществе обработки сигналов, известной как двухканальный поддиапазонный кодер с использованием сопряженных квадратурных фильтров или квадратурных зеркальных фильтров (QMF).

Алгоритм разложения начинается с сигнала s, затем вычисляются координаты A1 и D1, а затем координаты A2 и D2 и так далее.
Алгоритм реконструкции, называемый обратным дискретным вейвлет-преобразованием (IDWT), начинается с координат _AJ и _DJ, затем вычисляет координаты _AJ-1, а затем с помощью координат _AJ-1 и _DJ-1 вычисляет координаты _AJ-2 и так далее.

В этом разделе рассматриваются следующие темы:

Фильтры, используемые для расчета DWT и IDWT

Для ортогонального вейвлета в фреймворке мультирешений мы начинаем с масштабной функции, а затем с вейвлет-функции. Одним из фундаментальных отношений является двухмасштабное отношение (уравнение расширения или уравнение уточнения):

$\frac{}{} 12start(\frac{}{} x2) \underset{}{}_{} =∑n∈Zwnϕ (x$ − n)

Все фильтры, используемые в DWT и IDWT, тесно связаны с последовательностью

(_wn) _n∊Z

Ясно, что при компактной поддержке, последовательность (_wn) является конечной и может рассматриваться как фильтр. Фильтр W, который называется фильтром масштабирования (ненормализованным), является

Конечная импульсная характеристика (КИХ)
Длины 2N
Суммы 1
Нормы $\frac{}{\sqrt{12}}$
Нормы 1
Фильтр нижних частот

Например, для db3 фильтр масштабирования,

load db3 
db3
    db3 =
    0.2352   0.5706   0.3252  -0.0955  -0.0604   0.0249

sum(db3)
    ans =
         1.0000

norm(db3)
    ans =
         0.7071

Из фильтра W мы определяем четыре фильтра FIR длиной 2N и нормой 1, организованных следующим образом.

Фильтры	Низкопроходная	Высокопроходимая
Разложение	Lo_D	Hi_D
Реконструкция	Lo_R	Hi_R

Четыре фильтра вычисляются с использованием следующей схемы.

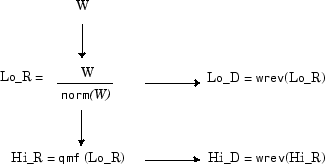
где qmf является таким, что Hi_R и Lo_R являются квадратурными зеркальными фильтрами (т.е. Hi_R (k) = (-1) ^kLo_R (2N + 1 - k)) для k = 1, 2,..., 2N.

Обратите внимание, что wrev разворачивает коэффициенты фильтра. Так что Hi_D и Lo_D - это также квадратурные зеркальные фильтры. Вычисление этих фильтров выполняется с помощью orthfilt. Далее мы иллюстрируем эти свойства с помощью db6 вейвлет.

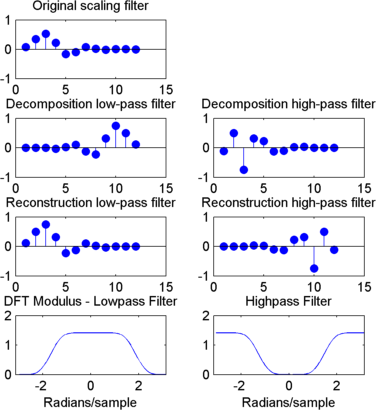
Загрузите фильтр масштабирования экстремальной фазы Daubechies и постройте график коэффициентов.

load db6;
subplot(421); stem(db6,'markerfacecolor',[0 0 1]);
title('Original scaling filter');

Использовать orthfilt для возврата фильтров анализа (разложения) и синтеза (реконструкции).

Получить дискретные преобразования Фурье (DFT) фильтров анализа нижних и верхних частот. Постройте график модуля DFT.

LoDFT = fft(Lo_D,64);
HiDFT = fft(Hi_D,64);
freq = -pi+(2*pi)/64:(2*pi)/64:pi;
subplot(427); plot(freq,fftshift(abs(LoDFT)));
set(gca,'xlim',[-pi,pi]); xlabel('Radians/sample');
title('DFT Modulus - Lowpass Filter')
subplot(428); plot(freq,fftshift(abs(HiDFT)));
set(gca,'xlim',[-pi,pi]); xlabel('Radians/sample');
title('Highpass Filter');

Алгоритмы

Учитывая сигнал s длиной N, DWT состоит максимум из _log2N каскадов. Начиная с s, первый шаг производит два набора коэффициентов: коэффициенты аппроксимации cA1 и коэффициенты детализации cD1. Эти векторы получают сверткой s с фильтром нижних частот Lo_D для аппроксимации и с фильтром верхних частот Hi_D для детализации с последующим диадическим прореживанием.

Точнее, первый шаг -

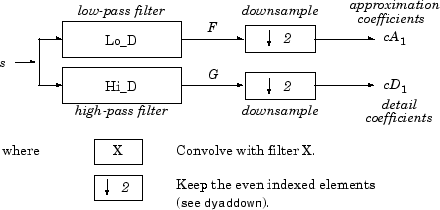
Длина каждого фильтра равна 2L. Результатом свертки сигнала длины N с фильтром длины 2L является N + 2L-1. Поэтому сигналы F и G имеют длину N + 2L - 1. После понижающей дискретизации на 2 векторы коэффициентов _cA1 и _cD1 имеют длину

$⌊ \frac{N}{−} 12$ + L ⌋.

Следующий шаг разбивает коэффициенты аппроксимации, cA1 на две части, используя одну и ту же схему, заменяя s на cA1 и производя cA2 и cD2 и так далее.

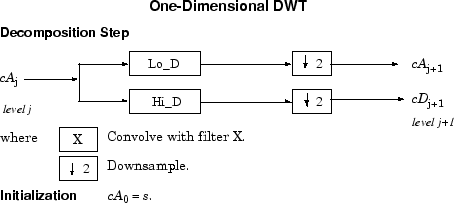
Итак, вейвлет-разложение сигнала s, анализируемого на уровне j, имеет следующую структуру: [_cAj, _cDj,..., cD1_].

Эта структура содержит для J = 3 терминальные узлы следующего дерева.

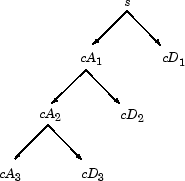
И наоборот, начиная с cAj и cDj, IDWT восстанавливает cAj-1, инвертируя этап разложения путем вставки нулей и свертывания результатов с фильтрами реконструкции.
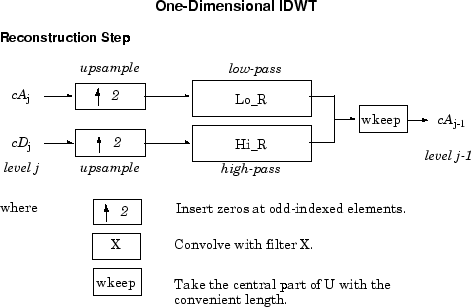
Для изображений возможен аналогичный алгоритм для двумерных вейвлетов и функций масштабирования, полученных из 1-D вейвлетов тензориальным произведением.
Такого рода 2-D DWT приводит к разложению коэффициентов аппроксимации на уровне j в четырёх компонентах: аппроксимации на уровне j + 1 и деталей в трёх ориентациях (горизонтальной, вертикальной и диагональной).
Следующие диаграммы описывают основные этапы разложения и реконструкции изображений.

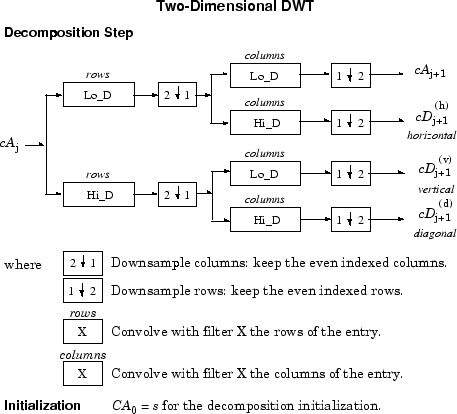
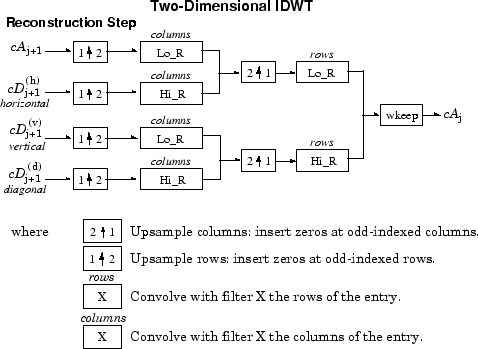
Так, для J = 2 2-D вейвлет-дерево имеет следующий вид.

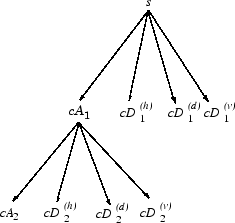
Наконец, давайте упомянем, что для биоргональных вейвлетов одни и те же алгоритмы содержат, но фильтры разложения, с одной стороны, и фильтры реконструкции, с другой стороны, получены из двух различных функций масштабирования, связанных с двумя анализами множественных решений в дуальности.

В этом случае фильтры для разложения и восстановления обычно имеют различную нечетную длину. Такая ситуация имеет место, например, для биорогональных вейвлетов «сплайнов», используемых в панели инструментов. При заполнении нулями четыре фильтра могут быть расширены таким образом, что они будут иметь одинаковую четную длину.

Почему такой алгоритм существует?

В предыдущем параграфе описываются алгоритмы, предназначенные для сигналов или изображений конечной длины. Чтобы понять обоснование, мы должны рассмотреть сигналы бесконечной длины. Способы расширения данного сигнала конечной длины описаны в Border Effects.

Обозначим h = Lo_R и g = Hi_R и сосредоточимся на 1-D случае.

Сначала мы обосновываем, как перейти от уровня j к уровню j + 1, для вектора аппроксимации. Это основной шаг алгоритма разложения для вычисления аппроксимаций. Детали вычисляются таким же образом с использованием фильтра g вместо фильтра h.

Пусть (_Ak ^(j)) k∊Z быть координатами вектора Aj:

$_{Aj} = \underset{}{}_{ kAk}^{} {(j)}_{ϕj}$ , k

и _Ak ^{(j +} 1) координаты _{вектора} _Aj + 1:

$_{Aj+1} = \underset{}{}_{ kAk}^{} {(j+1)}_{ϕj+1}$ , k

_Ak ^{(j +} 1) рассчитывается по формуле

$_{Ак}^{(j +} \underset{)}{1}_{}_{}^{}$ =∑nhn−2kAn (j)

Эта формула напоминает формулу свертки.

Расчет очень прост.

Давайте определим

$\overset{h˜}{} (k) = h (− k) и_{}^{Fk} \underset{j}{(} {\overset{+}{}}_{1)}^{}$ =∑nh˜k−nAn (j).

Последовательность F ^{(j +} 1) является отфильтрованным выходом последовательности ^A (j) с помощью $\overset{}{}$ фильтра h˜.

Получаем

_Ak ^{(j +} 1) ₌^{F2k (}j + 1)

Мы должны взять четные значения индекса F. Это понижающая выборка.

Последовательность A ^{(j +} 1) является пониженной версией последовательности ^{F (}j + 1).

Инициализация выполняется с использованием _Ak ⁽⁰) = s (k), где s (k) - значение сигнала в момент времени k.

Есть несколько причин для этого неожиданного результата, все из которых связаны с ситуацией множественного разрешения и с несколькими свойствами функций ,

Давайте рассмотрим некоторые из них.

Семейство $(_{} ϕ0,k,k∈Z)$ образовано ортонормированными функциями. В результате для любого j семейство $(_{} ϕj,k,k∈Z)$ является ортонормированным.
Двойное индексированное семейство

$(_{} ψj,k,j∈Z,k∈Z)$
ортонормированный.
Для любого j, $(_{ϕj, k}, k∈Z)$ ортогональные к $(_{{ψj}^{'}, k}, j^{}'\leq j, k∈Z$ ).
Между двумя последовательными шкалами мы имеем фундаментальное отношение, называемое двойным отношением.

Двухмасштабное отношение (Twin-Scale Relation) для

$_{} \underset{}{}_{}_{ϕ1,0=∑k∈Zhkϕ0,k}$

$_{} \underset{}{}_{}_{ϕj+1,0=∑k∈Zhkϕj,k}$

Это отношение вводит h-фильтр алгоритма $(_{hn} \sqrt{=_{}}$ 2startn). Дополнительные сведения см. в разделе Фильтры, используемые для расчета DWT и IDWT.
Мы проверяем, что:
1. Координата _{фj + 1,0} на _фj,k _равна hk и не зависит от j.
2. Координата фj _{+ 1,} n на _фj, k равна $_{〈}_{}_{}$ ϕj+1,n,ϕj,k〉=hk−2n .
Эти отношения обеспечивают ингредиенты для алгоритма.
До сих пор мы использовали фильтр h. Фильтр верхних частот g используется в отношении сдвоенных шкал, связывающих функции, связанные между собой. Между двумя последовательными шкалами мы имеем следующую двойную фундаментальную связь.

Двухмасштабная связь между

$_{} \underset{}{}_{}_{ψ1,0=∑k∈Zgkϕ0,k}$

$_{} \underset{}{}_{}_{ψj+1,0=∑k∈Zgkϕj,k}$
После этапа разложения мы оправдываем теперь алгоритм реконструкции, построив его. Упростим нотацию. Начав с A1 и D1, изучим A0 = A1 + _Dj1. Процедура является такой же, чтобы вычислить A = _Aj ₊ 1 + _Dj + 1.
Определим _αn, _δn, $_{}^{αk0}$ по
$_{A1} = \sum_{}_{}_{nanϕ1,} n D1 = ∑_{} \underset{nδnψ1}{},_{}_{n A0 =}_{ kak0ϕ0}, \underset{}{k}_{}^{}_{}$
Оценим $_{}^{}$ координаты αk0 как
$\begin{array}{l} _{}^{}_{}_{}_{}_{}_{}_{}_{}_{}_{} \\ \underset{}{}_{}_{}_{} \underset{}{}_{}_{}_{} \\ \underset{}{}_{}_{} \underset{}{}_{}_{ak0=〈A0,ϕ0,k〉=〈A1+D1,ϕ0,k〉=〈A1,ϕ0,k〉+〈D1,ϕ0,k〉=∑nan〈ϕ1,n,ϕ0,k〉+∑nδn〈ψ1,n,ϕ0,k〉=∑nanhk−2n+∑nδngk−2n} \end{array}$

Двухмасштабное отношение (Twin-Scale Relation) для
$_{} \underset{}{}_{}_{ϕ1,0=∑k∈Zhkϕ0,k}$	$_{} \underset{}{}_{}_{ϕj+1,0=∑k∈Zhkϕj,k}$

Двухмасштабная связь между
$_{} \underset{}{}_{}_{ψ1,0=∑k∈Zgkϕ0,k}$	$_{} \underset{}{}_{}_{ψj+1,0=∑k∈Zgkϕj,k}$

Мы сосредоточим наше исследование на первой сумме $_{}_{}_{∑nanhk−2n};$ вторая сумма $_{}_{}_{∑nδngk−2n}$ обрабатывается аналогичным образом.

Вычисления легко организованы, если отметить, что (принимая k = 0 в предыдущих формулах, делает вещи проще)

$\begin{array}{l} \underset{}{}_{}_{} \sumnanh-2n= . . ._{+}_{a} -_{}_{} 1h2_{+}_{} {a0h0}_{} +_{} a1h \\ - 2_{+}_{} a2h_{−} 4_{} +_{.} . ._{= .} . ._{} +_{a} −_{} 1h2_{+}_{} 0h1 \end{array}$ + a0h0 + 0h − 1 + a1h − 2 + 0h − 3 + a2h − 4 +...

Если мы преобразуем $(_{αn})$ последовательность в новую последовательность ${\overset{}{(}}_{} α˜n$ ), определенную

_{..., α–1, 0, α0, 0, α1, 0, α2, 0, ...} это именно

${\overset{}{}}_{}_{} {\overset{}{}}_{} a˜2n=an,a˜2n+1=0$

Тогда

$\underset{}{}_{}_{} \underset{}{} {\overset{}{}}_{}_{∑nanh−2n=∑na˜nh−n}$

и путем продления

$\underset{}{}_{}_{} \underset{}{} {\overset{}{}}_{}_{∑nanhk−2n=∑na˜nhk−n}$

С тех пор

$_{}^{} \underset{}{} {\overset{}{}}_{}_{} \underset{}{} {\overset{}{}}_{}_{ak0=∑na˜nhk−n+∑nδ˜ngk−n}$

этапы реконструкции:

Замените последовательности α и δ увеличенными версиями α˜ и $\overset{δ˜}{}$ вставкой нулей.
Фильтровать по h и g соответственно.
Суммировать полученные последовательности.

1-D Возможности вейвлета

Основные объекты 1-D

	Объекты	Описание
Сигнал в исходное время	s _Ak, 0 ≤ k ≤ j _Dk, 1 ≤ k ≤ j	Исходный сигнал Приближение на уровне k Детализация на уровне k
Коэффициенты во времени, связанном со шкалой	_cAk, 1 ≤ k ≤ j _cDk, 1 ≤ k ≤ j [_cAj, _cDj,..., cD1_]	Коэффициенты аппроксимации на уровне k Коэффициенты детализации на уровне k Вейвлет-декомпозиция на уровне j, j ≥ 1

Объекты

Описание

Сигнал в исходное время

_Ak, 0 ≤ k ≤ j

_Dk, 1 ≤ k ≤ j

Исходный сигнал

Приближение на уровне k

Детализация на уровне k

Коэффициенты во времени, связанном со шкалой

_cAk, 1 ≤ k ≤ j

_cDk, 1 ≤ k ≤ j

[_cAj, _cDj,..., cD1_]

Коэффициенты аппроксимации на уровне k

Коэффициенты детализации на уровне k

Вейвлет-декомпозиция на уровне j, j ≥ 1

Возможности анализа-декомпозиции

Цель	Вход	Продукция	Файл
Одноуровневая декомпозиция	s	cA1, cD1	`dwt`
Одноуровневая декомпозиция	_cAj	_cAj ₊ 1, _cDj + 1	`dwt`
Разложение	s	[_cAj, _cDj,..., cD1_]	`wavedec`

Возможности синтеза-реконструкции

Цель	Вход	Продукция	Файл
Одноуровневая реконструкция	cA1, cD1	s или A0	`idwt`
Одноуровневая реконструкция	_cAj ₊ 1, _cDj + 1	_cAj	`idwt`
Полная реконструкция	[_cAj, _cDj,..., cD1_]	s или A0	`waverec`
Выборочная реконструкция	[_cAj, _cDj,..., cD1_]	_Аль, _Дм	`wrcoef`

Утилиты структуры декомпозиции

Цель	Вход	Продукция	Файл
Извлечение коэффициентов детализации	[_cAj, _cDj,..., cD1_]	_cDk, 1 ≤ k ≤ j	`detcoef`
Извлечение коэффициентов аппроксимации	[_cAj, _cDj,..., cD1_]	_cAk, 0≤ k ≤ j	`appcoef`
Перекомпозиция структуры разложения	[_cAj, _cDj,..., cD1_]	[_cAk, _cDk,..., cD1_] 1 ≤ k ≤ j	`upwlev`

Для иллюстрации режима командной строки для 1-D возможностей см. раздел Анализ 1-D с помощью командной строки..

2-D Возможности вейвлета

Основные объекты 2-D

	Объекты	Описание
Изображение в исходном разрешении	s	Исходное изображение
	A0	Аппроксимация на уровне 0
	_Ak, 1 ≤ k ≤ j	Приближение на уровне k
	_Dk, 1 ≤ k ≤ j	Сведения на уровне k
Коэффициенты в разрешении, связанном с масштабом	_cAk, 1 ≤ k ≤ j	Коэффициенты аппроксимации на уровне k
	_cDk, 1 ≤ k ≤ j	Коэффициенты детализации на уровне k
	[_cAj, _cDj,..., cD1_]	Вейвлет-декомпозиция на уровне j

_Dk означает $[_{Dk}^{(h}),_{}^{Dk} (v_{)}^{,} Dk$ (d)], горизонтальные, вертикальные и диагональные детали на уровне k.

То же самое относится к _cDk, который обозначает $[_{cDk}^{(h}),_{}^{cDk} (v)_{,}^{} cDk$ (d)].

Файлы 2-D аналогичны файлам для 1-D случая, но с 2 добавляется в конце команды.

Например, idwt становится idwt2. Дополнительные сведения см. в разделе 1-D вейвлет-возможностей.

Для иллюстрации режима командной строки для 2-D возможностей см. Анализ и сжатие вейвлетного изображения.

Ссылки

[1] Маллат, С. Г. «Теория декомпозиции сигналов с множественным разрешением: вейвлет-представление», транзакции IEEE по анализу шаблонов и машинному интеллекту. Том 11, выпуск 7, июль 1989 года, стр. 674-693.

Документация