Масштабирование до частоты
В этом примере показано изменение псевдочастоты при удвоении масштаба.
Постройте вектор весов с 10 голосами на октаву в течение пяти октав.
vpo = 10; no = 5; a0 = 2^(1/vpo); ind = 0:vpo*no; sc = a0.^ind;
Убедитесь, что диапазон шкал охватывает пять октав.
log2(max(sc)/min(sc))
ans = 5.0000
При построении шкалы можно использовать курсор данных, чтобы подтвердить, что шкала с индексом 10 в два раза больше шкалы с n. Установите y-галочки, чтобы отметить каждую октаву.
plot(ind,sc) title('Scales') xlabel('Index') ylabel('Scale') grid on set(gca,'YTick',2.^(0:5))
Преобразуйте шкалы в псевдопереходы для действительного вейвлета Морле. Во-первых, предположим, что период выборки равен 1.
pf = scal2frq(sc,"morl"); T = [sc(:) pf(:)]; T = array2table(T,'VariableNames',{'Scale','Pseudo-Frequency'}); disp(T)
Scale Pseudo-Frequency
______ ________________
1 0.8125
1.0718 0.75809
1.1487 0.70732
1.2311 0.65996
1.3195 0.61576
1.4142 0.57452
1.5157 0.53605
1.6245 0.50015
1.7411 0.46666
1.8661 0.43541
2 0.40625
2.1435 0.37904
2.2974 0.35366
2.4623 0.32998
2.639 0.30788
2.8284 0.28726
3.0314 0.26803
3.249 0.25008
3.4822 0.23333
3.7321 0.2177
4 0.20313
4.2871 0.18952
4.5948 0.17683
4.9246 0.16499
5.278 0.15394
5.6569 0.14363
6.0629 0.13401
6.498 0.12504
6.9644 0.11666
7.4643 0.10885
8 0.10156
8.5742 0.094761
9.1896 0.088415
9.8492 0.082494
10.556 0.07697
11.314 0.071816
12.126 0.067006
12.996 0.062519
13.929 0.058332
14.929 0.054426
16 0.050781
17.148 0.047381
18.379 0.044208
19.698 0.041247
21.112 0.038485
22.627 0.035908
24.251 0.033503
25.992 0.03126
27.858 0.029166
29.857 0.027213
32 0.025391
Предположим, что данные дискретизируются на частоте 100 Гц. Создайте таблицу с масштабами, соответствующими псевдочастотами и периодами. Так как на октаву приходится 10 голосов, отображайте каждую десятую строку в таблице. Обратите внимание, что для каждого удвоения шкалы псевдочастотность разрезается пополам.
Fs = 100; DT = 1/Fs; pf = scal2frq(sc,"morl",DT); T = [sc(:)/Fs pf(:) 1./pf(:)]; T = array2table(T,'VariableNames',{'Scale','Pseudo-Frequency','Period'}); T(1:vpo:end,:)
ans=6×3 table
Scale Pseudo-Frequency Period
_____ ________________ ________
0.01 81.25 0.012308
0.02 40.625 0.024615
0.04 20.313 0.049231
0.08 10.156 0.098462
0.16 5.0781 0.19692
0.32 2.5391 0.39385
Обратите внимание на наличие коэффициента Δt = 1Fs вscal2frq. Это необходимо для достижения надлежащего преобразования масштаба в частоту. Δt необходим для правильной регулировки необработанных шкал. Например, с:
f = scal2frq(1,'morl',0.01);Вы действительно спрашиваете, что происходит с центральной частотой материнского вейвлета Морле, если вы расширяете вейвлет на 0,01. Другими словами, каково влияние на центральную частоту, если вместо (смотреть на (). Δt обеспечивает правильный поправочный коэффициент для шкал.
Вы могли бы получить те же результаты, сначала преобразовав шкалы в их скорректированные размеры, а затем используя scal2frq without specifying .
scadjusted = sc.*0.01;
pf2 = scal2frq(scadjusted,'morl');
max(pf-pf2)ans = 0
В примере показано, как создать контурный график CWT с использованием приблизительных частот в Гц.
Создайте сигнал, состоящий из двух синусоидальных волн с непересекающейся поддержкой аддитивного шума. Предположим, что сигнал дискретизирован на частоте 1 кГц.
Fs = 1000; t = 0:1/Fs:1-1/Fs; x = 1.5*cos(2*pi*100*t).*(t<0.25)+1.5*cos(2*pi*50*t).*(t>0.5 & t<=0.75); x = x+0.05*randn(size(t));
Получите CWT входного сигнала и постройте график результата.
[cfs,f] = cwt(x,Fs); contour(t,f,abs(cfs).^2); axis tight; grid on; xlabel('Time'); ylabel('Approximate Frequency (Hz)'); title('CWT with Time vs Frequency');
Существует только приблизительный ответ на связь между масштабом и частотой.
При вейвлет-анализе способ соотнести масштаб с частотой состоит в том, чтобы определить центральную частоту вейвлета, Fc, и использовать следующее соотношение:
Fca
где
a - масштаб.
Fc - центральная частота импульса в Гц.
Fa - псевдочастота, соответствующая шкале а, в Гц.
Идея состоит в том, чтобы связать с данным вейвлетом чисто периодический сигнал частоты Fc. Частота, максимизирующая преобразование Фурье модуля импульса, равна Fc. centfrq функция вычисляет центральную частоту для заданного вейвлета. Из приведенного выше соотношения можно видеть, что масштаб обратно пропорционален псевдочастоте. Например, если масштаб увеличивается, вейвлет становится более распределенным, что приводит к более низкой псевдочастоте.
Некоторые примеры соответствия между центральной частотой и вейвлетом показаны на следующем рисунке.
Центральные частоты для реальных и сложных вейвлетов
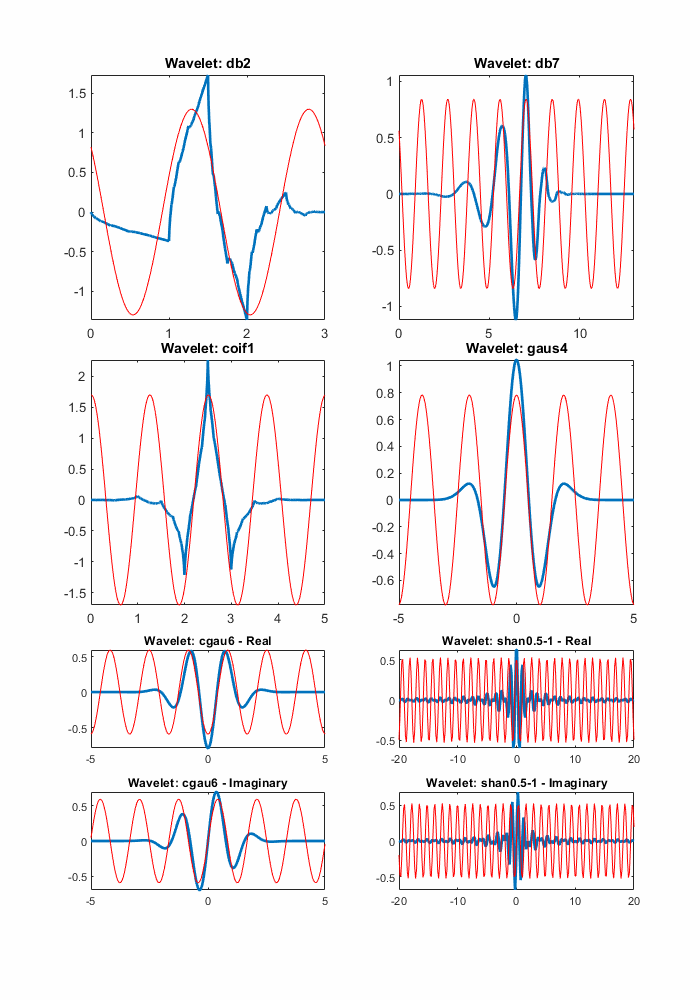
[1] Абри, П. Онделеттс и турбулентность. Multirésolutions, алгоритмы décomposition, инварианс d 'échelles et signaux de pression. Дидро, Editeurs des sciences et des arts, Париж, 1997.