Одноуровневое дискретное 2-D вейвлет-преобразование
dwt2 вычисляет одноуровневую 2-D вейвлет-декомпозицию. Выдержать сравнение dwt2 с wavedec2 что может быть более полезным для вашего приложения. Разложение выполняется по отношению к конкретному вейвлету (см. wfilters для получения дополнительной информации) или конкретных фильтров вейвлет-декомпозиции.
[ вычисляет одноуровневую 2-ю дискретную небольшую волну преобразовывает (DWT) входных данных cA,cH,cV,cD] = dwt2(X,wname)X с использованием wname вейвлет. dwt2 возвращает матрицу коэффициентов аппроксимации cA и матрицы коэффициентов детализации cH, cV, и cD (горизонтальный, вертикальный и диагональный соответственно).
[ вычисляет одноуровневый 2-D DWT с режимом расширения cA,cH,cV,cD] = dwt2(___,'mode',extmode)extmode. Включить этот аргумент после всех остальных аргументов.
Примечание
Для gpuArray входы, поддерживаемые режимы: 'symh' ('sym') и 'per'. Все 'mode' варианты, за исключением 'per' преобразуются в 'symh'. См. пример одноуровневого 2-D дискретного вейвлет-преобразования на графическом процессоре.
Загрузка и отображение изображения.
load woman
imagesc(X)
colormap(map)
Получить одноуровневое 2-D дискретное вейвлет-преобразование изображения с использованием порядка 4 symlet и периодического расширения.
[cA,cH,cV,cD] = dwt2(X,'sym4','mode','per');
Отображение коэффициентов детализации по вертикали и коэффициентов аппроксимации.
imagesc(cV)
title('Vertical Detail Coefficients')
imagesc(cA)
title('Approximation Coefficients')
Загрузка и отображение изображения.
load sculpture imagesc(X) colormap gray
Создайте фильтры разложения нижних и верхних частот для вейвлета Хаара.
[LoD,HiD] = wfilters('haar','d');
Используйте фильтры для одноуровневой 2-D вейвлет-декомпозиции. Используйте симметричное удлинение в половине точки. Отображение коэффициентов аппроксимации и детализации.
[cA,cH,cV,cD] = dwt2(X,LoD,HiD,'mode','symh'); subplot(2,2,1) imagesc(cA) colormap gray title('Approximation') subplot(2,2,2) imagesc(cH) colormap gray title('Horizontal') subplot(2,2,3) imagesc(cV) colormap gray title('Vertical') subplot(2,2,4) imagesc(cD) colormap gray title('Diagonal')
Сведения о поддерживаемых графических процессорах см. в документе Поддержка графического процессора по выпуску (Панель инструментов параллельных вычислений).
Загрузите изображение. Поместите изображение на графический процессор с помощью gpuArray. Сохраните текущий режим расширения.
load mask imgg = gpuArray(X); origMode = dwtmode('status','nodisp');
Использовать dwtmode для изменения режима расширения на заполнение нулем. Получение одноуровневого 2-D DWT изображения на графическом процессоре с помощью db2 вейвлет.
dwtmode('zpd','nodisp') [cA,cH,cV,cD] = dwt2(imgg,'db2');
Текущий режим расширения zpd не поддерживается для gpuArray вход. Поэтому DWT вместо этого выполняется с помощью sym режим расширения. Подтвердите это, взяв DWT из imgg с установленным режимом расширения sym и сравните с предыдущим результатом.
[cAsym,cHsym,cVsym,cDsym] = dwt2(imgg,'db2','mode','sym'); [max(abs(cA(:)-cAsym(:))) max(abs(cH(:)-cHsym(:))) ... max(abs(cV(:)-cVsym(:))) max(abs(cD(:)-cDsym(:)))]
ans =
0 0 0 0
Неподдерживаемый режим расширения, указанный в качестве входного аргумента, преобразуется в 'sym'. Подтвердите, что получение DWT из imgg с 'mode' установить в неподдерживаемый режим также по умолчанию sym режим расширения.
[cA,cH,cV,cD] = dwt2(imgg,'db2','mode','spd'); [max(abs(cA(:)-cAsym(:))) max(abs(cH(:)-cHsym(:))) ... max(abs(cV(:)-cVsym(:))) max(abs(cD(:)-cDsym(:)))]
ans =
0 0 0 0
Измените текущий режим расширения на периодический. Получение одноуровневого DWT изображения на графическом процессоре с помощью db2 вейвлет.
dwtmode('per','nodisp') [cA,cH,cV,cD] = dwt2(imgg,'db2');
Подтверждение текущего режима внутреннего абонента per поддерживается для gpuArray вход.
[cAper,cHper,cVper,cDper] = dwt2(imgg,'db2','mode','per'); [max(abs(cA(:)-cAper(:))) max(abs(cH(:)-cHper(:))) ... max(abs(cV(:)-cVper(:))) max(abs(cD(:)-cDper(:)))]
ans =
0 0 0 0
Восстановите режим расширения в исходное значение.
dwtmode(origMode,'nodisp')Алгоритм 2-D вейвлет-декомпозиции для изображений аналогичен одномерному случаю. Двумерные вейвлет-функции и функции масштабирования получают, принимая тензорные произведения одномерных вейвлет-функций и функций масштабирования. Такой вид двумерного DWT приводит к разложению коэффициентов аппроксимации на уровне j в четырёх компонентах: аппроксимация на уровне j + 1, а детали в трёх ориентациях (горизонтальной, вертикальной и диагональной). Следующая диаграмма описывает основные шаги разложения для изображений.
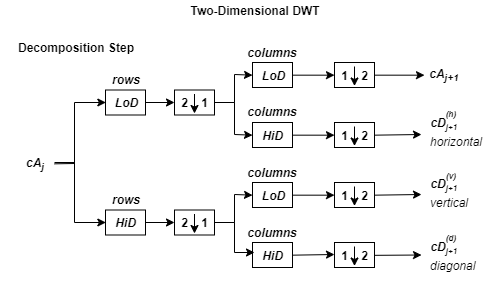
где
- Столбцы с пониженной выборкой: сохранить столбцы с четной индексацией
- Строки с пониженной выборкой: сохранить строки с четным индексом
- Свернуть с фильтром X строки записи
- Свернуть с фильтром X столбцы записи
Разложение инициализируется установкой коэффициентов аппроксимации, равных изображению s: cA0 = s.
Примечание
Чтобы справиться с эффектами конца сигнала, введенными алгоритмом на основе свертки, 1-D и 2-D DWT используют глобальную переменную, управляемую dwtmode. Эта переменная определяет тип используемого режима расширения сигнала. Возможные опции включают заполнение нулем и симметричное расширение, которое является режимом по умолчанию.
[1] Даубехии, Ингрид. Десять лекций по вейвлетам. Серия региональных конференций CBMS-NSF по прикладной математике 61. Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1992.
[2] Маллат, С.Г. «Теория разложения сигнала с множественным разрешением: вейвлет-представление». IEEE Transactions on Pattern Analysis and Machine Intelligence 11, No. 7 (июль 1989 года): 674-93. https://doi.org/10.1109/34.192463.
[3] Мейер, Я. Вейвлетс и Операторы. Перевёл Д. Х. Сэлинджер. Кембридж, Великобритания: Cambridge University Press, 1995.