Приложение 2-D непрерывного вейвлет-преобразования (CWT) позволяет анализировать данные изображения и экспортировать результаты этого анализа в рабочую область MATLAB ®. Приложение предоставляет все функциональные возможности функций командной строкиcwtft2 и cwtftinfo2. Доступ к приложению 2-D CWT в галерее приложений путем выбора Wavelet Design & Analysis в разделе Signal Processing and Communications или ввода
cwtfttool2
в командной строке MATLAB.
2-D непрерывное вейвлет-преобразование является представлением 2-D данных (данных изображения) в 4 переменных: расширение, поворот и положение. Расширение и вращение - вещественные скаляры, а положение - 2-D вектор с вещественными элементами. Пусть x обозначает двухэлементный вектор вещественных чисел. Если
ℝ2)
интегрируемо квадратом в самолете, 2-й CWT определен как
a∈ℝ+, x,b∈ℝ2
где штрих обозначает комплексный сопряженный, а r, является матрицей вращения 2-D
0,2π)
2-й CWT - космическое масштабное изображение изображения. Можно просмотреть инверсию масштаба и угла поворота, взятые вместе как пространственно-частотная переменная, что дает 2-D CWT интерпретацию как пространственно-частотное представление. Для всех допустимых 2-х небольших волн 2-й CWT действует как местный фильтр для изображения по своим масштабам и положения. Если вейвлет изотропен, в анализе нет зависимости от угла. Мексиканский шляпочный вейвлет является примером изотропного вейвлета. Изотропные вейвлеты пригодны для точечного анализа изображений. Если вейвлет анизотропен, то в анализе существует зависимость от угла, и 2-D CWT действует как локальный фильтр для изображения по масштабу, положению и углу. Вейвлет Коши является примером анизотропного вейвлета. В области Фурье это означает, что пространственной частотной опорой вейвлета является выпуклый конус с вершиной в начале координат. Анизотропные вейвлеты пригодны для обнаружения направленных признаков в изображении. Пример различия между изотропными и анизотропными вейвлетами см. в разделе Двухмерный CWT шумного шаблона.
В этом примере показано, как анализировать изображение с помощью приложения 2-D CWT.
Загрузите треугольное изображение в рабочую область MATLAB.
imdata = imread('triangle.jpg');Запустите приложение 2-D CWT, выбрав Wavelet Design & Analysis в разделе Signal Processing and Communications галереи приложений. В разделе 2-D выберите Непрерывное вейвлет-преобразование 2-D. Либо введите
cwtfttool2
в командной строке MATLAB.
Выберите Файл - > Импорт данных для импорта imdata переменная.
От Wavelet выберите кошистый вейвлет.
Для параметров «Углы» и «Масштаб» выберите параметр «Вручную».
Щелкните Задать (Define), чтобы задать вектор углов. Выберите Ручной (Manual) в меню Type раскрывающийся список и укажите вектор углов от 0 до 7*pi/8 радианы с приращениями pi/8 радианы, 0:pi/8:(7*pi)/8. Нажмите кнопку Применить (Apply), чтобы применить выбранные углы.
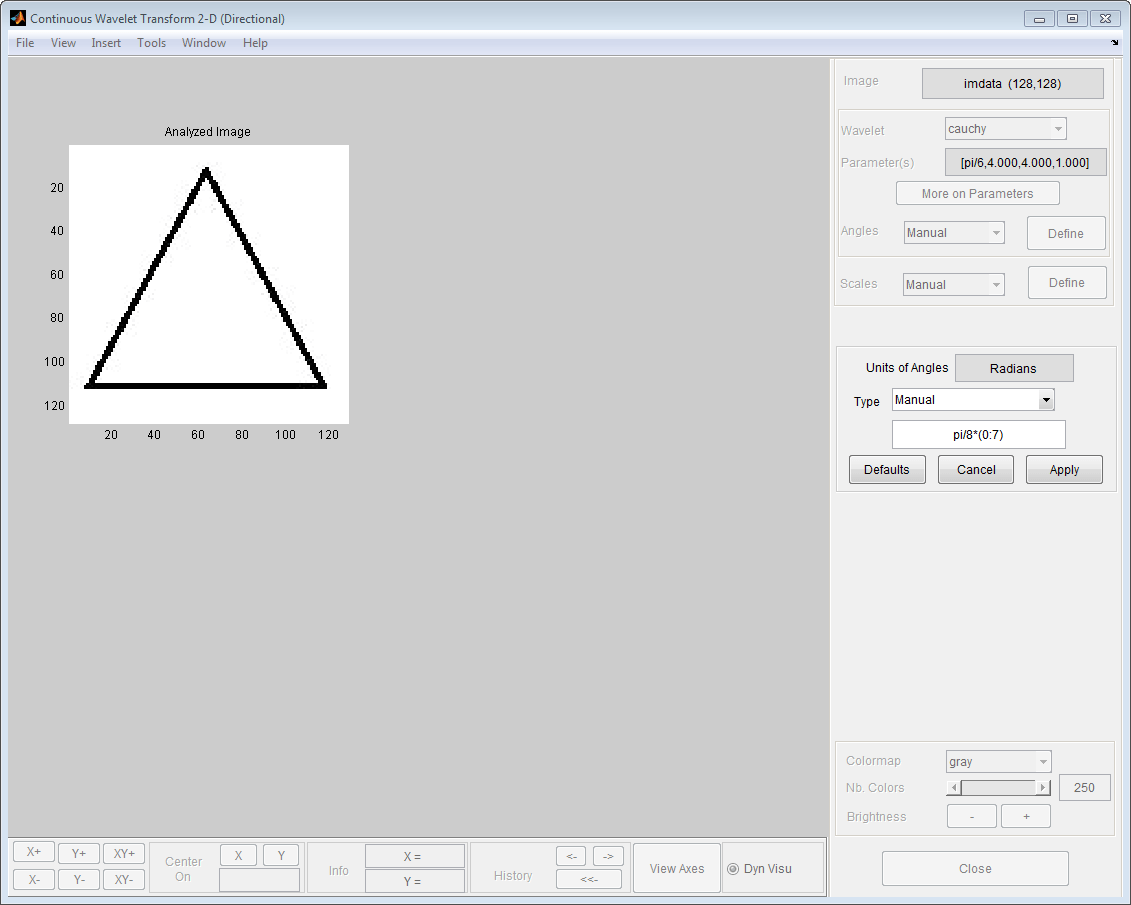
Щелкните Задать (Define), чтобы задать вектор масштаба от 0,5 до 4 с шагом 0,5. Выберите Линейный (Linear) из списка Type раскрывающийся список. Установите первую шкалу равной 0,5, зазор между двумя шкалами равной 0,5 и число шкал равной 8. Эквивалентно, можно выбрать Вручную (Manual) из Type раскрывающийся список и укажите вектор масштабов как 0.5:0.5:4. Нажмите кнопку Применить (Apply), чтобы применить выбранный масштаб.
Щелкните Анализ (Analyze), чтобы получить 2-D CWT.
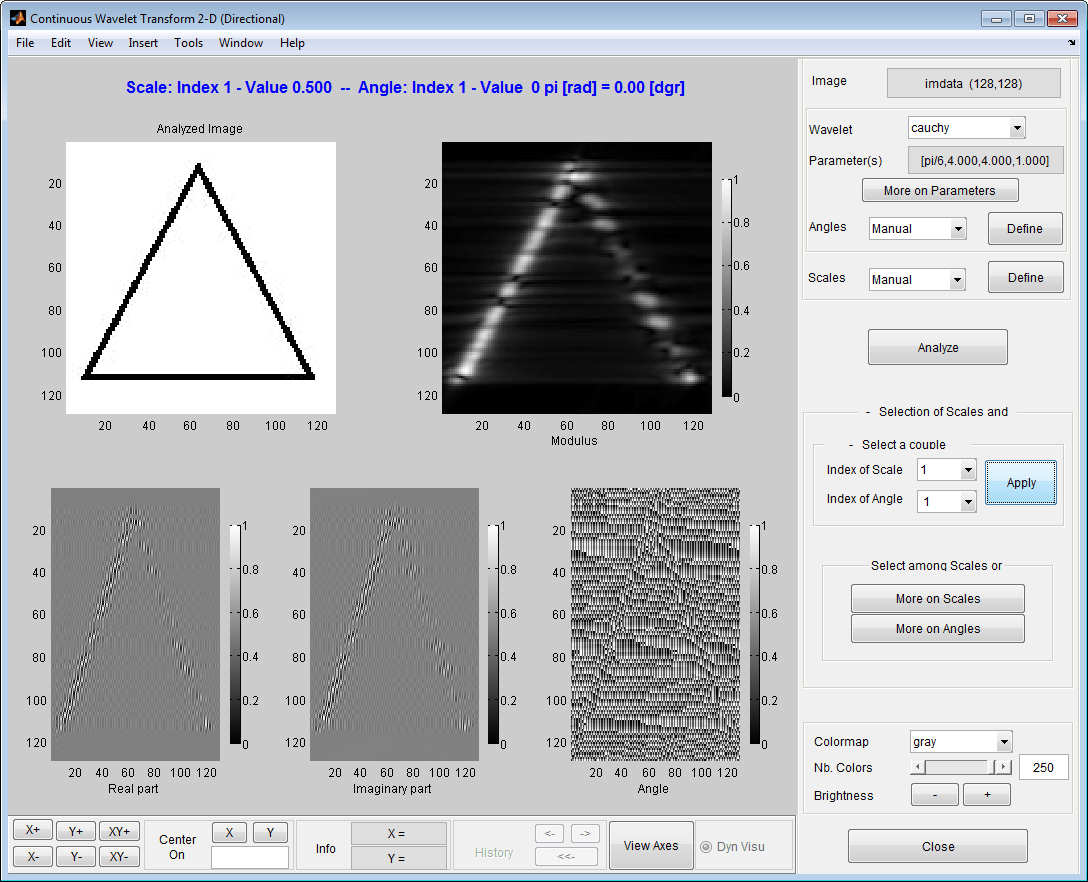
Установите Index of Scale Чтобы стать 1, щелкните Дополнительно на углах (More on Angles). Щелкните Фильм (Movie), чтобы перейти к заданным вручную углам для 2-D коэффициентов CWT в масштабе 0,5.
Выберите Файл - > Экспорт данных - > Экспорт структуры CWTFT в рабочую область для экспорта анализа в рабочую область MATLAB. Описание полей структуры можно найти в ссылке на функцию дляcwtft2.