Пограничные эффекты

Классически DWT определяется для последовательностей с длиной некоторой степени 2, и необходимы различные способы расширения выборок других размеров. Способы расширения сигнала включают заполнение нулем, гладкое заполнение, периодическое расширение и репликацию граничных значений (симметризацию).

Базовый алгоритм для DWT не ограничен диадической длиной и основан на простой схеме: свертка и понижающая дискретизация. Как обычно, при выполнении свертки по сигналам конечной длины возникают граничные искажения.

Расширения сигналов: заполнение нулем, симметризация и гладкое заполнение

Чтобы справиться с искажениями границ, граница должна рассматриваться иначе, чем другие части сигнала.

Для решения этой проблемы доступны различные способы, называемые «вейвлетами на интервале» [1]. Эти интересные конструкции эффективны в теории, но не вполне удовлетворительны с практической точки зрения.

Часто предпочтительно использовать простые схемы, основанные на расширении сигнала на границах. Это включает в себя вычисление нескольких дополнительных коэффициентов на каждой стадии процесса разложения, чтобы получить совершенную реконструкцию. Следует отметить, что расширение необходимо на каждой стадии процесса разложения.

Подробная информация об обосновании этих схем приведена в главе 8 книги «Вейвлеты и банки фильтров» (Strang and Nguyen) [2].

Доступны следующие режимы расширения сигналов (см. dwtmode):

Заполнение нулем ('zpd'): Этот метод используется в версии DWT, приведенной в предыдущих разделах, и предполагает, что сигнал равен нулю за пределами исходной поддержки.
Недостатком заполнения нулем является то, что на границе искусственно создаются разрывы.
Симметризация ('sym'): Этот метод предполагает, что сигналы или изображения могут быть восстановлены за пределами их первоначальной поддержки путем симметричной репликации граничных значений.
Это режим вейвлет-преобразования по умолчанию на панели инструментов.
Симметризация имеет недостаток искусственного создания разрывов первой производной на границе, но этот метод хорошо работает в целом для изображений.
Плавное заполнение порядка 1 ('spd'или 'sp1'): Этот метод предполагает, что сигналы или изображения могут быть восстановлены за пределами их первоначальной поддержки с помощью простой экстраполяции производной первого порядка: заполнение с использованием линейного расширения, соответствующего первым двум и последним двум значениям.
Гладкое заполнение хорошо работает в целом для гладких сигналов.
Плавное заполнение порядка 0 ('sp0'): Этот метод предполагает, что сигналы или изображения могут быть восстановлены за пределами их первоначальной поддержки с помощью простой постоянной экстраполяции. Для расширения сигнала это повторение первого значения слева и последнего значения справа.
Периодическое заполнение (1) ('ppd'Этот метод предполагает, что сигналы или изображения могут быть восстановлены за пределами их первоначальной поддержки посредством периодического расширения.
Недостатком периодического заполнения является то, что на границе искусственно создаются разрывы.

DWT, связанный с этими пятью режимами, слегка избыточен. Однако IDWT обеспечивает идеальную реконструкцию любого из пяти предыдущих режимов независимо от режима расширения, используемого для DWT.

Периодическое заполнение (2) ('per'Если длина сигнала нечетная, сигнал сначала расширяется путем добавления дополнительной выборки, равной последнему значению справа. Затем выполняют минимальное периодическое удлинение с каждой стороны. Для изображений существует такое же правило. Этот режим расширения используется для SWT (1-D & 2-D).

Этот последний режим создает вейвлет-декомпозицию наименьшей длины. Но режим расширения, используемый для IDWT, должен быть таким же, чтобы обеспечить идеальную реконструкцию.

Прежде чем рассматривать иллюстративный пример, сравним некоторые свойства теоретического дискретного вейвлет-преобразования с фактическим DWT.

Теоретический DWT применяется к сигналам, которые определены на интервале времени бесконечной длины (Z). Для ортогонального вейвлета это преобразование имеет следующие желательные свойства:

Консервация нормы
Пусть cA и cD - приближение и детализация коэффициентов DWT сигнала бесконечной длины X. Тогда сохраняется l2-норма:
‖ ^X‖2 = ‖ ^cA‖2 + ‖ ^cD‖2
Ортогональность
Пусть A и D - восстановленное приближение и деталь. Затем A и D ортогональны и
‖ ^X‖2 = ‖ ^A‖2 + ‖ D‖2
Идеальная реконструкция
X = A + D

Поскольку DWT применяется к сигналам, которые определены в интервале времени конечной длины, для разложения необходимо расширение, а для реконструкции необходимо усечение.

Обеспечить решающее свойство 3 (идеальная реконструкция) для произвольного выбора

Длина сигнала
Небольшая волна
Режим внутренней линии

свойства 1 и 2 могут быть потеряны. Эти свойства имеют значение true для расширенного сигнала, длина которого обычно превышает длину исходного сигнала. Так что всегда сохраняется только идеальное свойство реконструкции. Тем не менее, если DWT выполняется с использованием периодического режима расширения ('per') и если длина сигнала делится на ^2J, где J - максимальное разложение уровня, свойства 1, 2 и 3 остаются истинными.

Практические соображения

Открыть сценарий

Итеративный шаг DWT состоит из фильтрации с последующим понижением дискретизации:

Для получения коэффициентов аппроксимации примените фильтр нижних частот, а затем уменьшите выборку на два.
Для получения коэффициентов детализации примените фильтр верхних частот, а затем уменьшите выборку на два.

Таким образом, концептуально, число коэффициентов аппроксимации составляет половину числа выборок, и аналогично для коэффициентов детализации.

В реальном мире мы имеем дело с сигналами конечной длины. С желанием применить теоретический алгоритм DWT к практическому, должен быть решен вопрос граничных условий: как должен быть расширен сигнал?

Перед изучением различных сценариев сохраните текущий режим удлинения границы.

origmodestatus = dwtmode('status','nodisplay');

Периодический, мощность 2

Рассмотрим следующий пример. Загрузить noisdopp данные. Сигнал имеет 1024 выборки, что является мощностью 2. Использовать dwtmode для установки режима расширения на периодический. Затем использовать wavedec для получения DWT уровня 3 сигнала с использованием ортогонального db4 вейвлет.

load noisdopp;
x = noisdopp;
lev = 3;
wav = 'db4';
dwtmode('per','nodisp')
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         128         128         256         512        1024

Вектор бухгалтерского учета bk содержит число коэффициентов по уровням. На каждом этапе количество коэффициентов детализации уменьшается точно в 2 раза. В конце находятся $1024/2^3 = 128$ коэффициенты аппроксимации.

Сравните $l^2$ -norms.

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))

l2-norm difference: 9.0658e-09

Получение восстановленных аппроксимаций и деталей путем установки в 0 соответствующих сегментов вектора коэффициентов c и принимают обратный DWT.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

Проверьте ортогональность.

fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))

Orthogonality difference 1.816e-08

Проверьте идеальную реконструкцию.

fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

Perfect reconstruction difference: 1.674e-11

Сохраняются три теоретических свойства DWT.

Периодическая, не мощность 2

Теперь получите трехуровневый DWT сигнала с 1026 выборками. Используйте тот же самый вейвлет и режим расширения, что и выше. Число коэффициентов на этапе n не разделяет равномерно длину сигнала.

x = [0 0 noisdopp];
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         129         129         257         513        1026

Проверьте сохранение $l^2$ -norm, ортогональность и совершенную реконструкцию.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))
fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))
fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

l2-norm difference: -1.4028
Orthogonality difference -0.3319
Perfect reconstruction difference: 1.6858e-11

Идеальная реконструкция удовлетворена, но $l^2$ -норм и ортогональность не сохранены.

Непериодический, мощность 2

Получите трехуровневый DWT сигнала с помощью 1024. Используйте тот же самый вейвлет, что и выше, но на этот раз измените режим расширения на плавное расширение порядка 1. Число коэффициентов на этапе n не разделяет равномерно длину сигнала.

dwtmode('sp1','nodisp')
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         134         134         261         516        1026

Проверьте сохранение $l^2$ -norm, ортогональность и совершенную реконструкцию.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))
fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))
fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

l2-norm difference: -113.58
Orthogonality difference -2.678
Perfect reconstruction difference: 1.6372e-11

Опять же, удовлетворена только идеальная реконструкция.

Восстановите исходный режим расширения.

dwtmode(origmodestatus,'nodisplay');

Для поддержки идеальной реконструкции для произвольного выбора длины сигнала, вейвлета и режима расширения мы используем кадры вейвлетов.

Кадр - это набор функций $\{\phi_k\}$ , удовлетворяющих следующему условию: существуют константы $0 < A \leq B$ , такие, что для любой функции $f$ рамочное неравенство держится: $A{\|f\|}^2 \leq \Sigma_k {|\langle f,\phi_k\rangle|}^2 \leq B {\|f\|}^2.$

Функции в кадре обычно не являются линейно независимыми. Это означает, что функция $f$ не имеет уникального расширения в. $\phi_k$ Daubechies [3] показывает, что если является $\{\tilde{\phi}_k\}$ двойственным кадром и для $f = \Sigma_{k\in K} c_k\phi_k$ некоторых, а $c = \left(c_k\right)\in l^2(K)$ если не все равны $c_k$ , то. $\langle f,\tilde{\phi}_k\rangle$ $\Sigma_{k\in K}{|c_k|}^2 \geq \Sigma_{k\in K}{|\langle f,\tilde{\phi}_k\rangle|}^2$

Если, $A = B$ кадр называется плотным кадром. Если $A = B = 1$ и $\|\phi_k\|^2 = 1$ для всех, $\phi_k$ кадр является ортонормированным базисом. Если, $A \neq B$ то энергия не обязательно сохраняется, и общее число коэффициентов может превышать длину сигнала. Если режим расширения является периодическим, вейвлет является ортогональным, и длина сигнала делится на, $2^J$ где - $J$ максимальный уровень вейвлет-разложения, удовлетворяются все три теоретических свойства DWT.

Произвольные расширения

Открыть сценарий в реальном времени

Интересно заметить, что если используется произвольное расширение, и разложение выполняется с использованием схемы свертки-понижающей дискретизации, идеальная реконструкция восстанавливается с использованием idwt или idwt2.

Создайте сигнал и получите фильтры, связанные с db9 вейвлет.

x = sin(0.3*[1:451]);
w = 'db9';
[LoD,HiD,LoR,HiR] = wfilters(w);

Добавить и добавить length(LoD) случайные числа к сигналу. Постройте график исходного и расширенного сигналов.

lx = length(x);
lf = length(LoD);
ex = [randn(1,lf) x randn(1,lf)];
ymin = min(ex);
ymax = max(ex);
subplot(2,1,1)
plot(lf+1:lf+lx,x)
axis([1 lx+2*lf ymin ymax]);
title('Original Signal')
subplot(2,1,2)
plot(ex)
title('Extended Signal')
axis([1 lx+2*lf ymin ymax])

Figure contains 2 axes. Axes 1 with title Original Signal contains an object of type line. Axes 2 with title Extended Signal contains an object of type line.

Используйте фильтры низкочастотной и высокочастотной вейвлет-декомпозиции для получения одноуровневой вейвлет-декомпозиции расширенного сигнала.

la = floor((lx+lf-1)/2);
ar = wkeep(dyaddown(conv(ex,LoD)),la);
dr = wkeep(dyaddown(conv(ex,HiD)),la);

Подтвердите идеальную реконструкцию сигнала.

xr = idwt(ar,dr,w,lx);
err0 = max(abs(x-xr))

err0 = 5.4700e-11

Сравнение внутренних различий

Теперь рассмотрим различия между первыми тремя способами как для 1-D, так и для 2-D сигналов.

Заполнение нулями

С помощью приложения Wavelet Analysis мы рассмотрим эффекты заполнения нулем.

В подсказке MATLAB ® введите
```
dwtmode('zpd')
```
В приглашении MATLAB введите waveletAnalyzer.
Появится вейвлет-анализатор.
Выберите пункт меню Wavelet 1-D. Появляется инструмент дискретного вейвлет-анализа для 1-D данных сигнала.
В меню Файл выберите опцию Пример анализа и выберите Основные сигналы > с db2 на уровне 5 > Два близлежащих разрыва.
Выберите Режим отображения: Показать и прокрутить.
Коэффициенты детализации ясно показывают конечные эффекты сигнала.
Симметричное расширение
В приглашении MATLAB введите
```
dwtmode('sym')
```
Выберите пункт меню Wavelet 1-D.
Появляется инструмент дискретного вейвлет-анализа для 1-D данных сигнала.
В меню Файл выберите опцию Пример анализа и выберите Основные сигналы > с db2 на уровне 5 > Два близлежащих разрыва .
Выберите Режим отображения: Показать и прокрутить.
Коэффициенты детализации ясно показывают конечные эффекты сигнала.
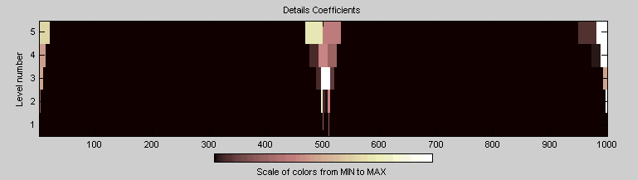
Гладкое заполнение
В приглашении MATLAB введите
```
dwtmode('spd')
```
Выберите пункт меню Wavelet 1-D.
Появляется инструмент дискретного вейвлет-анализа для 1-D данных сигнала.
В меню Файл выберите опцию Пример анализа и выберите Основные сигналы > с db2 на уровне 5 > Два близлежащих разрыва.
Выберите Режим отображения: Показать и прокрутить.
Коэффициенты детализации показывают, что конечные эффекты сигнала отсутствуют, и разрывы хорошо обнаружены.

Расширения изображения

Открыть сценарий в реальном времени

Рассмотрим пример изображения. Сохраните текущий режим расширения. Загрузить и отобразить geometry изображение.

origmodestatus = dwtmode('status','nodisplay');
load geometry
nbcol = size(map,1);
colormap(pink(nbcol))
image(wcodemat(X,nbcol))

Figure contains an axes. The axes contains an object of type image.

Заполнение нулями

Установите режим расширения на нуль и выполните разложение изображения на уровень 3 с помощью sym4 вейвлет. Затем реконструируйте приближение уровня 3.

lev = 3;
wname = 'sym4';
dwtmode('zpd','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Figure contains an axes. The axes contains an object of type image.

Симметричное расширение

Установите режим расширения на симметричное расширение и выполните разложение изображения на уровень 3 с помощью sym4 вейвлет. Затем реконструируйте приближение уровня 3.

dwtmode('sym','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Figure contains an axes. The axes contains an object of type image.

Гладкое заполнение

Установите режим расширения для сглаживания заполнения и выполните разложение изображения до уровня 3 с помощью sym4 вейвлет. Затем реконструируйте приближение уровня 3.

dwtmode('spd','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Figure contains an axes. The axes contains an object of type image.

Восстановите исходный режим расширения.

dwtmode(origmodestatus,'nodisplay')

Ссылки

[1] Коэн, А., И. Даубехис, Б. Джаверт и П. Виал. «Анализ множественных решений, вейвлеты и быстрые алгоритмы на интервале». Comptes Rendus Acad. Sci. Paris Sér. A, том 316, стр. 417-421, 1993.

[2] Странг, G. и Т. Нгуен. Вейвлеты и банки фильтров. Уэлсли, Массачусетс: Уэлсли-Кембридж Пресс, 1996.

[3] Daubechies, I. Десять лекций по вейвлетам, серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: SIAM Ed, 1992.

См. также

dwtfilterbank | wavedec

Документация