Exponenta Banner
exponenta event banner

wavedec

1-D вейвлет-декомпозиция

свернуть все на странице

Синтаксис

[c, l] = wavedec (x, n, wname)
[c, l] = wavedec (x, n, LoD, HiD)

Описание

пример

[c,l] = wavedec(x,n,wname) возвращает вейвлет-декомпозицию 1-D сигнала x на уровне n использование вейвлета wname. Структура выходной декомпозиции состоит из вектора вейвлет-декомпозиции c и вектор бухгалтерского учета l, который содержит количество коэффициентов по уровню.

Примечание

Для gpuArray входы, поддерживаемые режимы: 'symh' ('sym') и 'per'. Если входным значением является gpuArray, режим расширения дискретного вейвлет-преобразования, используемый wavedec по умолчанию: 'symh' если текущий режим расширения не 'per'. См. пример многоуровневого дискретного вейвлет-преобразования на графическом процессоре.

[c,l] = wavedec(x,n,LoD,HiD) возвращает вейвлет-декомпозицию с использованием указанных фильтров низкочастотной и высокоскоростной вейвлет-декомпозиции LoD и HiDсоответственно.

Примеры

свернуть все

Открыть сценарий в реальном времени

Загрузите и постройте график одномерного сигнала.

load sumsin 
plot(sumsin)
title('Signal')

Figure contains an axes. The axes with title Signal contains an object of type line.

Выполните 3-уровневую вейвлет-декомпозицию сигнала, используя вейвлет порядка 2 Daubechies. Извлеките коэффициенты приближения грубого масштаба и коэффициенты детализации из разложения.

[c,l] = wavedec(sumsin,3,'db2');
approx = appcoef(c,l,'db2');
[cd1,cd2,cd3] = detcoef(c,l,[1 2 3]);

Постройте график коэффициентов.

subplot(4,1,1)
plot(approx)
title('Approximation Coefficients')
subplot(4,1,2)
plot(cd3)
title('Level 3 Detail Coefficients')
subplot(4,1,3)
plot(cd2)
title('Level 2 Detail Coefficients')
subplot(4,1,4)
plot(cd1)
title('Level 1 Detail Coefficients')

Figure contains 4 axes. Axes 1 with title Approximation Coefficients contains an object of type line. Axes 2 with title Level 3 Detail Coefficients contains an object of type line. Axes 3 with title Level 2 Detail Coefficients contains an object of type line. Axes 4 with title Level 1 Detail Coefficients contains an object of type line.

В этом примере используются:

Открыть сценарий в реальном времени

Сведения о поддерживаемых графических процессорах см. в документе Поддержка графического процессора по выпуску (Панель инструментов параллельных вычислений).

Загрузите шумный доплеровский сигнал. Поставьте сигнал на ГП с помощью gpuArray. Сохраните текущий режим расширения.

load noisdopp
noisdoppg = gpuArray(noisdopp);
origMode = dwtmode('status','nodisp');

Использовать dwtmode для изменения режима расширения на заполнение нулем. Получение трехуровневого DWT сигнала на GPU с помощью db4 вейвлет.

dwtmode('zpd','nodisp')
[c,l] = wavedec(noisdoppg,3,'db4');

Текущий режим расширения zpd не поддерживается для gpuArray вход. Поэтому DWT вместо этого выполняется с помощью sym режим расширения. Для подтверждения установите режим внутреннего абонента в значение sym и принять DWT из noisdoppg, затем сравните с предыдущим результатом.

dwtmode('sym','nodisp')
[csym,lsym] = wavedec(noisdoppg,3,'db4');
[max(abs(c-csym)) max(abs(l-lsym))]
ans =

     0     0

Установить текущий режим расширения в значение per и получить трехуровневый DWT noisdopp. Режим внутренней линии per поддерживается для gpuArray вход. Подтвердите, что результат отличается от sym результаты.

dwtmode('per','nodisp')
[cper,lper] = wavedec(noisdoppg,3,'db4');
[length(csym) ; length(cper)]
ans = 2×1

        1044
        1024


[lsym ; lper]
ans = 2×5

         134         134         261         515        1024
         128         128         256         512        1024

Восстановите режим расширения в исходное значение.

dwtmode(origMode,'nodisp')

Входные аргументы

свернуть все

Входной сигнал, заданный как вектор.

Типы данных: single | double
Поддержка комплексного номера: Да

Уровень разложения, заданный как положительное целое число. wavedec не применяет ограничение максимального уровня. Использовать wmaxlev чтобы гарантировать, что вейвлет-коэффициенты свободны от граничных эффектов. Если граничные эффекты не являются проблемой в приложении, необходимо установить правильное правило n меньше или равно fix(log2(length(x))).

Типы данных: single | double

Анализ вейвлета, заданного как вектор символа или скаляр строки.

Примечание

wavedec поддерживает только вейвлеты типа 1 (ортогональные) или типа 2 (биортогональные). Посмотрите wfilters для списка ортогональных и биоргональных вейвлетов.

Фильтры вейвлет-декомпозиции, задаваемые как пара действительных векторов чётной длины. LoD является фильтром разложения нижних частот, и HiD - фильтр разложения верхних частот. Длины LoD и HiD должно быть равным. Посмотрите wfilters для получения дополнительной информации.

Типы данных: single | double

Выходные аргументы

свернуть все

Вектор вейвлет-разложения, возвращаемый как вектор. Вектор бухгалтерского учета l содержит число коэффициентов по уровням. Вектор разложения и вектор учета организованы, как на этой диаграмме разложения уровня 3.

Типы данных: single | double

Вектор учета, возвращаемый как вектор положительных целых чисел. Вектор учета используется для синтаксического анализа коэффициентов в векторе вейвлет-разложения. c по уровню.

Типы данных: single | double

Алгоритмы

Учитывая сигнал s длиной N, DWT состоит максимум из log2 N шагов. Начиная с s, первый шаг производит два набора коэффициентов: коэффициенты аппроксимации cA1 и коэффициенты детализации cD1. Свертывание s с фильтром нижних частот LoD и фильтр верхних частот HiD, с последующим диадическим прореживанием (понижающей дискретизацией), приводит к коэффициентам аппроксимации и детализации соответственно.

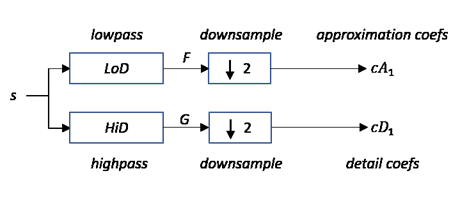
где

  • - Свернуть с фильтром X

  • ↓2 - Понижение (сохранить четные элементы)

Длина каждого фильтра равна 2n. Если N = длина (длины), сигналы F и G имеют длину N + 2n − 1, а коэффициенты cA1 и cD1 имеют длину

пол (N − 12) + n.

Следующий шаг разбивает коэффициенты аппроксимации, cA1 на две части, используя одну и ту же схему, заменяя s на cA1 и производя cA2 и cD2 и так далее.

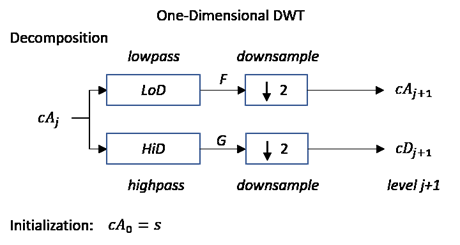
Вейвлет-разложение сигнала s, анализируемого на уровне j, имеет следующую структуру: [cAj, cDj,..., cD1].

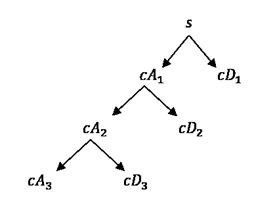
Эта структура содержит для j = 3 конечные узлы следующего дерева:

Ссылки

[1] Daubechies, I. Десять лекций по вейвлетам, серия региональных конференций CBMS-NSF по прикладной математике. Филадельфия, Пенсильвания: SIAM Ed, 1992.

[2] Маллат, С. Г. «Теория разложения сигнала с множественным разрешением: вейвлет-представление», транзакции IEEE по анализу шаблонов и машинному интеллекту. Том 11, выпуск 7, июль 1989 года, стр. 674-693.

[3] Мейер, Я. Вейвлетс и Операторы. Перевёл Д. Х. Сэлинджер. Кембридж, Великобритания: Cambridge University Press, 1995.

Расширенные возможности

..

См. также

| | | | | | |

Представлен до R2006a

Документация инструментария вейвлет

Поддержка