В Wavelet Data Compression мы рассмотрели аспекты, конкретно связанные со сжатием с использованием вейвлетов. Однако в дополнение к алгоритмам, связанным с вейвлетами, такими как DWT и IDWT, необходимо использовать другие ингредиенты, относящиеся к режиму квантования и типу кодирования, чтобы иметь дело с истинным сжатием.
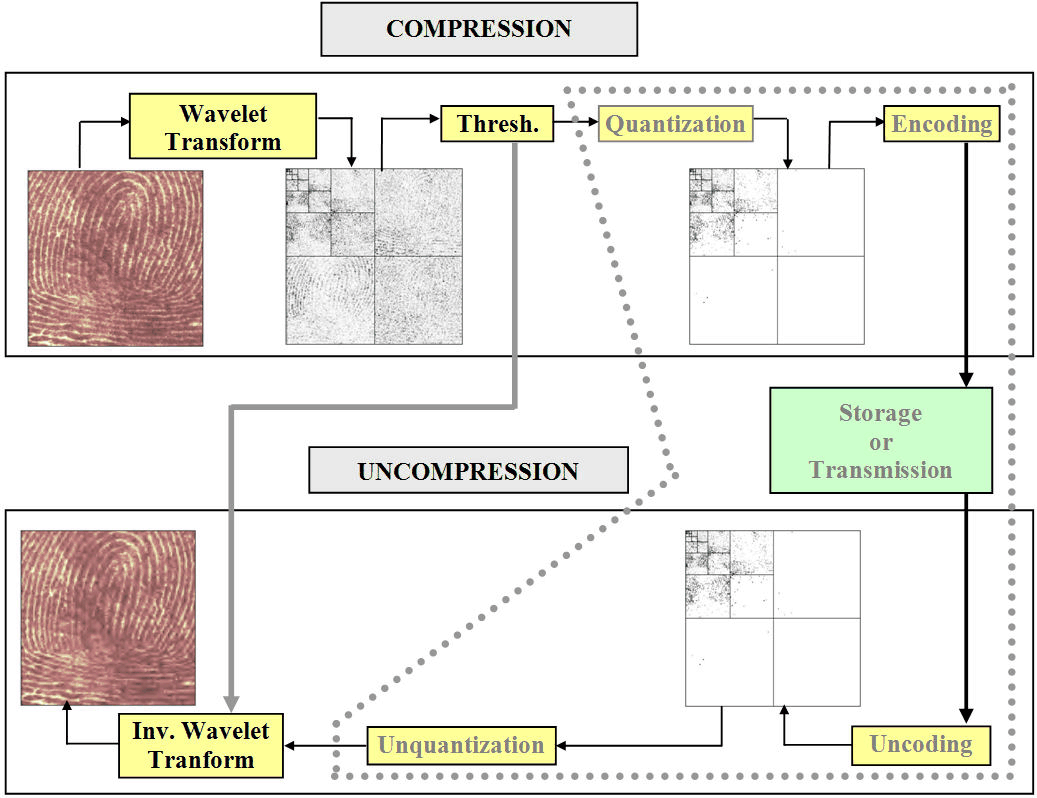
Этот более сложный процесс может быть представлен на следующем рисунке.
Покажем влияние квантования на визуализацию изображения отпечатка пальца. Это индексированное изображение соответствует матрице целых чисел в диапазоне от 0 до 255. Посредством квантования мы можем уменьшить количество цветов, которое здесь равно 256.
На следующем рисунке показано, как уменьшить число цветов с 256 до 16, используя значения исходного изображения.
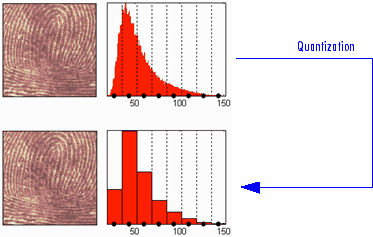
Мы можем видеть на этой фигуре:
Наверху
Слева: исходное изображение
Справа: соответствующая гистограмма значений
Внизу
Слева: реконструированное изображение
Справа: соответствующая гистограмма квантованных значений
Это квантование приводит к сжатию изображения. Действительно, с двоичным кодом фиксированной длины 8 бит на пиксель необходимы для кодирования 256 цветов и 4 бит на пиксель для кодирования 16 цветов. Мы отмечаем, что изображение, полученное после квантования, имеет хорошее качество. Однако в рамках истинного сжатия квантование используется не на исходном изображении, а на его вейвлет-декомпозиции.
Разложим изображение отпечатка пальца на уровне 4 вейвлетом Хаара. Гистограмма вейвлет-коэффициентов и квантованная гистограмма нормируются так, что значения изменяются между -1 и + 1. 15 интервалов квантования не имеют одинаковой длины.
На следующем рисунке показано, как уменьшить информацию путем привязки к значениям вейвлет-коэффициентов исходного изображения.
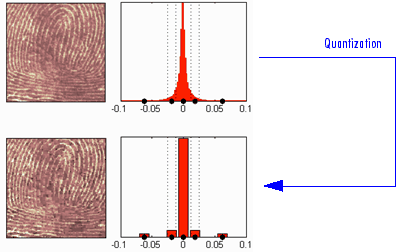
Мы можем видеть на этой фигуре:
Наверху
Слева: исходное изображение
Справа: соответствующая гистограмма (центральная часть) значений коэффициентов
Внизу
Слева: реконструированное изображение
Справа: соответствующая гистограмма (центральная часть) квантованных значений коэффициентов
Ключевой момент состоит в том, что гистограмма квантованных коэффициентов массово концентрируется в классе, центрированном в 0. Отметим, что вновь полученное изображение имеет хорошее качество.
Основные идеи, представленные выше, используются тремя способами, которые каскадируются в один этап, пороговое значение коэффициента (глобальное или по уровню) и кодирование квантованием. Фиксированное кодирование или кодирование Хаффмана может использоваться для квантования в зависимости от способа.
В следующей таблице обобщаются эти методы, часто называемые методами порогов коэффициентов (CTM), и приводится имя MATLAB ®, используемое истинными инструментами сжатия для каждого из них .
Имя MATLAB | Имя метода сжатия |
|---|---|
'gbl_mmc_f' | Глобальное пороговое значение коэффициентов и фиксированное кодирование |
'gbl_mmc_h' | Глобальное пороговое значение коэффициентов и кодирование Хаффмана |
'lvl_mmc' | Пороговое значение поддиапазона коэффициентов и кодирование Хаффмана |
Доступны более сложные способы, которые сочетают вейвлет-декомпозицию и квантование. Это основной принцип прогрессивных методов.
С одной стороны, прогрессивность дает возможность во время декодирования получать изображение, разрешение которого постепенно увеличивается. Кроме того, можно получить набор коэффициентов сжатия на основе длины сохраненного кода. Это сжатие обычно связано с потерей информации, но этот тип алгоритма также обеспечивает сжатие без потерь.
Такие методы основаны на трех идеях. Двумя первыми, уже упомянутыми, являются использование вейвлет-разложения для обеспечения разреженности (большое количество нулевых коэффициентов) и классические методы кодирования. Третья идея, решающая для использования вейвлетов при сжатии изображения, состоит в том, чтобы использовать в основном древовидную структуру вейвлет-разложения. Определённые коды, разработанные с 1993 по 2000 год, используют эту идею, в частности, введённый Шапиро алгоритм кодирования EZW. См. [Sha93] в разделе Ссылки.
EZW объединяет пошаговое пороговое значение и прогрессивное квантование, фокусируясь на более эффективном способе кодирования коэффициентов изображения, чтобы минимизировать степень сжатия. Два варианта SPIHT и STW (см. следующую таблицу) являются уточненными версиями основополагающего алгоритма EZW.
Следуя несколько другой цели, WDR (и уточнение ASWDR) фокусируется на том факте, что в целом некоторые части данного изображения требуют более точного кодирования, что приводит к лучшему восприятию результата, даже если обычно существует небольшая цена для оплаты с точки зрения степени сжатия.
Полный обзор этих прогрессивных методов находится в ссылке Уолкера [Wal99] в ссылках.
Следующая таблица суммирует эти методы, часто называемые методами значимости прогрессивных коэффициентов (PCSM), и дает кодированное имя MATLAB, используемое истинными инструментами сжатия для каждого из них.
Имя MATLAB | Имя метода сжатия |
|---|---|
'ezw' | Внедренный вейвлет Zerotree |
'spiht' | Задать разбиение в иерархических деревьях |
'stw' | Вейвлет дерева пространственной ориентации |
'wdr' | Уменьшение разности вейвлетов |
'aswdr' | Адаптивно сканированное уменьшение разности вейвлетов |
'spiht_3d' | Установка 3D секционирования в иерархических деревьях для цветных изображений |
Следующие количественные измерения и показатели качества восприятия полезны для анализа вейвлет-сигналов и изображений.
M S E - среднеквадратическая ошибка (MSE) - квадратичная норма разности между данными и аппроксимацией сигнала или изображения, деленная на количество элементов. MSE определяется следующим образом:
, j) | 2
Макс. погрешность - максимальная погрешность - максимальное абсолютное квадратичное отклонение в приближении сигнала или изображения.
Отношение L2-нормы - отношение L2-нормы - отношение брусковой L2-нормы сигнала или приближения изображения к входному сигналу или изображению. Для изображений изображение изменяется в виде вектора столбца перед выполнением L2-norm
P S N R - пиковое отношение сигнал/шум (PSNR) является мерой пиковой ошибки в децибелах. PSNR имеет значение только для данных, закодированных в терминах битов на выборку или битов на пиксель. Чем выше PSNR, тем лучше качество сжатого или восстановленного изображения. Типичные значения сжатия изображения с потерями находятся в диапазоне от 30 до 50 дБ. Если PSNR больше 40 дБ, то два изображения неотличимы. PSNR определяется следующим образом:
)
B P - отношение битов к пикселям (BPP) - количество битов, необходимое для хранения одного пикселя изображения. BPP представляет собой степень сжатия, умноженную на 8, предполагая один байт на пиксель (8 битов).
Comp Ratio - коэффициент сжатия - отношение количества элементов в сжатом изображении, деленное на количество элементов в исходном изображении, выраженное в процентах.
Примеры, иллюстрирующие режим командной строки и инструменты приложения для истинного сжатия, можно найти в Wavelet Compression for Images и на справочной странице для wcompress.
Более подробная информация о истинном сжатии для изображений и более точно о способах сжатия находится в [Wal99], [Sha93], [Sai96], [StrN96] и [Chr06]. См. раздел Ссылки.