Эта модель, doc_gray_code, показывает ссылку связи, использующую Серую 8-PSK модуляцию. Серое кодирование является методом, часто используемым в многоуровневых схемах модуляции, чтобы минимизировать вероятность битовой ошибки путем упорядочивания символов модуляции так, чтобы двоичные представления смежных символов отличались только на один бит.
Пример модели включает эти блоки:
Блок Random Integer Generator служит источником, создавая последовательность целых чисел.
Блок Integer to Bit Converter преобразует каждое целое число в соответствующее двоичное представление.
Блок AWGN Channel добавляет белый Гауссов шум к модулированным данным.
Блок M-PSK Demodulator Baseband демодулирует поврежденные данные.
Блок Bit to Integer Converter преобразует каждое двоичное представление в соответствующее целое число.
Одна копия блока Error Rate Calculation (с меткой Error Rate Calculation1 в этой модели) сравнивает демодулированные целочисленные данные с исходными исходными данными, получая статистику ошибок символов. Выход блока Error Rate Calculation является трехэлементным вектором, содержащим вычисленную частоту ошибок, количество наблюдаемых ошибок и объем обработанных данных.
Другая копия Error Rate Calculation библиотечного блока (маркированная Error Rate Calculation2 в этой модели) сравнивает демодулированные двоичные данные с двоичными представлениями исходных данных, получая статистику битовой ошибки.
В этой модели M-PSK Modulator Baseband блок:
Принимает двоичные входы, которые представляют целые числа от 0 до M − 1, где M является размером алфавита
Сопоставляет двоичные представления с точками созвездия с помощью Gray-кодированного упорядоченного расположения
Формирует комплексные выходные параметры фазора с единичной величиной, с равномерно расположенными фазами между 0 и 2 π (M − 1 )/ M
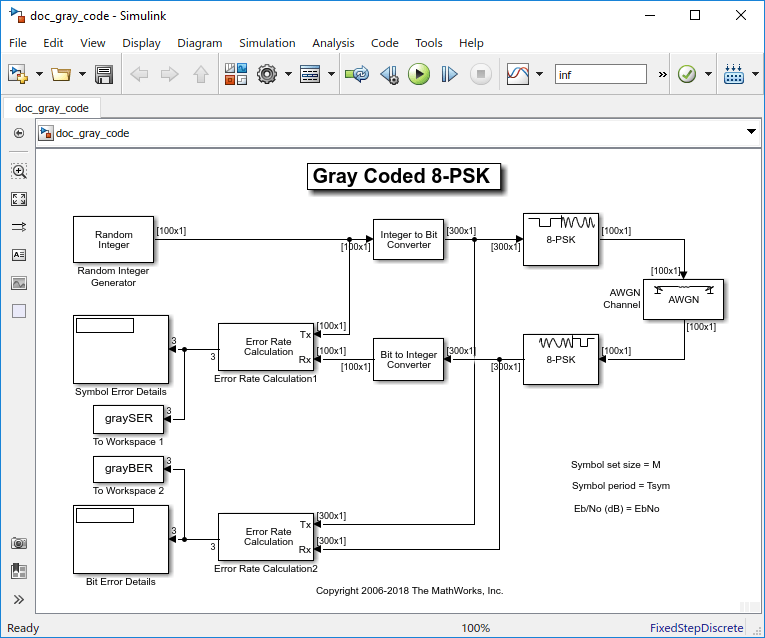
Таблица указывает, какие двоичные представления во входе соответствуют каким фазорам в выходе. Второй столбец таблицы является промежуточным представлением, которое блок использует в своих расчетах.
| Вход модулятора | Серокодированные Упорядоченные расположения | Выход модулятора |
|---|---|---|
000 | 0 | exp(0) = 1 |
001 | 1 | exp(jπ/4) |
010 | 3 | exp(j 3 <reservedrangesplaceholder0>/4) |
011 | 2 | exp(j 2 <reservedrangesplaceholder1>/4) = exp(jπ/2) |
100 | 7 | exp(j 7 <reservedrangesplaceholder0>/4) |
101 | 6 | exp(j 6 <reservedrangesplaceholder1>/4) = exp(j 3 <reservedrangesplaceholder0>/2) |
110 | 4 | exp(j 4 <reservedrangesplaceholder1>/4) = exp(<reservedrangesplaceholder0>) |
111 | 5 | exp(j 5 <reservedrangesplaceholder0>/4) |
Таблица ниже сортирует первые два столбца таблицы выше в соответствии с выходом значениями. Эта сортировка делает более ясным, что общий эффект этой подсистемы является отображением кода Грея, как показано на рисунке ниже. Заметьте, что числа во втором столбце таблицы ниже отображаются на рисунке в порядке против часовой стрелки.
| Выход модулятора | Вход модулятора |
|---|---|
exp(0) | 000 |
exp(j <reservedrangesplaceholder0>/4) | 001 |
exp(j 2 <reservedrangesplaceholder1>/4) = exp(jπ/2) | 011 |
exp(j 3 <reservedrangesplaceholder0>/4) | 010 |
exp(j 4 <reservedrangesplaceholder1>/4) = exp(<reservedrangesplaceholder0>) | 110 |
exp(j 5 <reservedrangesplaceholder0>/4) | 111 |
exp(j 6 <reservedrangesplaceholder1>/4) = exp(j 3 <reservedrangesplaceholder0>/2) | 101 |
exp(j 7 <reservedrangesplaceholder0>/4) | 100 |
Можно анализировать данные, которые приводит пример, чтобы сравнить теоретическую эффективность с эффективностью симуляции.
Теоретическая вероятность ошибки символа MPSK
где erfc является комплементарной функцией ошибки, Es/N0 является отношением энергии в спектральной плотности символа к степени шума, и M является количеством символов.
Чтобы определить вероятность битовой ошибки, вероятность символьной ошибки, PE, должна быть преобразована в эквивалентную ей битовую ошибку. Нет общей формулы для преобразования символа в битовую ошибку. Тем не менее, верхние и более низкие пределы легко установить. Фактическая вероятность битовой ошибки, Pb, может быть показана ограниченной
Нижний предел соответствует случаю, когда символы подверглись кодированию Грея. Верхний предел соответствует случаю чистого двоичного кодирования.
Чтобы протестировать схему модуляции кода Грея в этой модели, симулируйте модель грейкода для области значений Eb/N0 значений. Если вы хотите изучить частоты битовых ошибок, но не частоты символьных ошибок, то вы можете использовать bertool графический пользовательский интерфейс, как описано в Use Bit Error Rate Analysis App.
Остальная часть этого раздела исследует как бит, так и символьной ошибок и, следовательно, не использует bertool.
Поскольку увеличение значения Eb/N0 снижает количество произведенных ошибок, длина каждой симуляции должна быть увеличена, чтобы гарантировать, что статистика ошибок остается стабильной.
Использование sim (Simulink) для запуска Simulink® симуляция из MATLAB® Командное окно, следующий код генерирует данные для кривых частоты ошибок символа и частоты битовой ошибки. Он рассматривает Eb/N0 значения в области значений от 0 дБ до 12 дБ, в шагах 2 дБ.
M = 8; Tsym = 0.2; BERVec = []; SERVec = []; EbNoVec = [0:2:12]; for n = 1:length(EbNoVec); EbNo = EbNoVec(n); sim('doc_gray_code') ; SERVec(n,:) = graySER; BERVec(n,:) = grayBER; end;
После симуляции для полного набора Eb/N0 значений можно построить график результатов с помощью этих команд:
semilogy( EbNoVec,SERVec(:,1), 'o', EbNoVec, BERVec(:,1), '*' ); legend ( 'Symbol error rate', 'Bit error rate' ); xlabel ( 'Eb/No (dB)' ); ylabel( 'Error Probability' ); title ( 'Symbol and Bit Error Probability' );
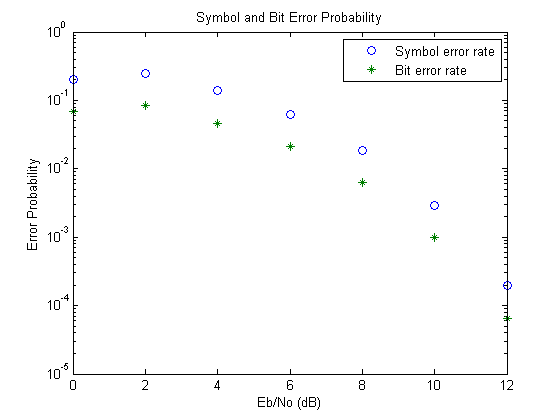
В качестве следующего упражнения, используя данные, полученные из berawgnможно построить график теоретических кривых на тех же осях с результатами симуляции. Можно также сравнить кодирование Грея с чистым двоичным кодированием, изменив блоки M-PSK Modulator Baseband и M-PSK Demodulator Baseband так, чтобы их параметры Constellation ordering Binary вместо Gray.