Поскольку тулбокс может обрабатывать сплайны с векторными коэффициентами, легко реализовать интерполяцию или приближение к сетчатым данным с помощью тензорных сплайнов продукта, как это должно быть показано на следующем рисунке. Можно также запустить пример «Двухфазные сплайны продукта».
Конечно, большая часть тензорного сплайна продукта приближение к данным с сеткой может быть получена непосредственно с помощью одной из команд конструкции сплайна, таких как spapi или csape, в этом тулбоксе, без беспокойства о деталях, обсуждаемых в этом примере. Скорее этот пример призван проиллюстрировать теорию, лежащую в основе конструкции тензорного продукта, и это будет полезно в ситуациях, не охватываемых конструкторскими командами в этом тулбоксе.
В этом разделе рассматриваются следующие аспекты проблемы тензорного сплайна продукта:
Рассмотрим, например, аппроксимацию методом наименьших квадратов к заданным z данных (i, j) = f (x (i), y (j)), i = 1: Nx, j = 1: Ny. Вы берете данные из функции, широко используемой Франке для проверки схем поверхностных подборов кривой (см. Р. Франке, «Критическое сравнение некоторых методов интерполяции данного , имеющего разброса», Военно-морская аспирантура Techn. Rep. NPS-53-79-003, март 1979). Его областью является модуль квадрат. Вы выбираете несколько более сайтов данных в x -направлении, чем y -направлении; кроме того, для лучшего определения вы используете более высокую плотность данных около контура.
x = sort([(0:10)/10,.03 .07, .93 .97]); y = sort([(0:6)/6,.03 .07, .93 .97]); [xx,yy] = ndgrid(x,y); z = franke(xx,yy);
Обработайте эти данные как поступающие от векторно-оцененной функции, а именно, функции y, значение которой в y (j) является векторной z (:, j), все j. Без особых причин принимайте решение аппроксимировать эту функцию векторным параболическим сплайном с тремя равномерно расположенными внутренними узлами. Это означает, что вы выбираете порядок сплайна и последовательность узлов для этого векторного сплайна как
ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);
а затем используйте spap2 для обеспечения наименьших квадратов, аппроксимированных к данным:
sp = spap2(knotsy,ky,y,z);
В эффекте вы находите одновременно дискретное приближение методом наименьших квадратов из S ky,knotsy каждому из Nx наборы данных
В частности, операторы
yy = -.1:.05:1.1; vals = fnval(sp,yy);
предоставить массив vals, чей вход vals(i,j) может быть взят в качестве приближения к значению f (x (<reservedrangesplaceholder8>), yy (<reservedrangesplaceholder6>)) основной функции f в сетчатой точке x (<reservedrangesplaceholder3>), yy (<reservedrangesplaceholder1>) потому что vals(:,j) - значение в yy (j) аппроксимации сплайн в sp.
Это видно на следующем рисунке, полученной по команде:
mesh(x,yy,vals.'), view(150,50)
Обратите внимание на использование vals.', в mesh команда, необходимая из-за MATLAB® матричный вид при построении графика массива. Это может быть серьезной проблемой в двухмерном приближении, потому что там принято думать о z (i, j) как о значении функции в точке (x (i), y (j)), в то время как MATLAB думает о z (i, j) как значении функции в точке (x (j), y (i)).
Семейство гладких кривых, притворяющихся поверхностью
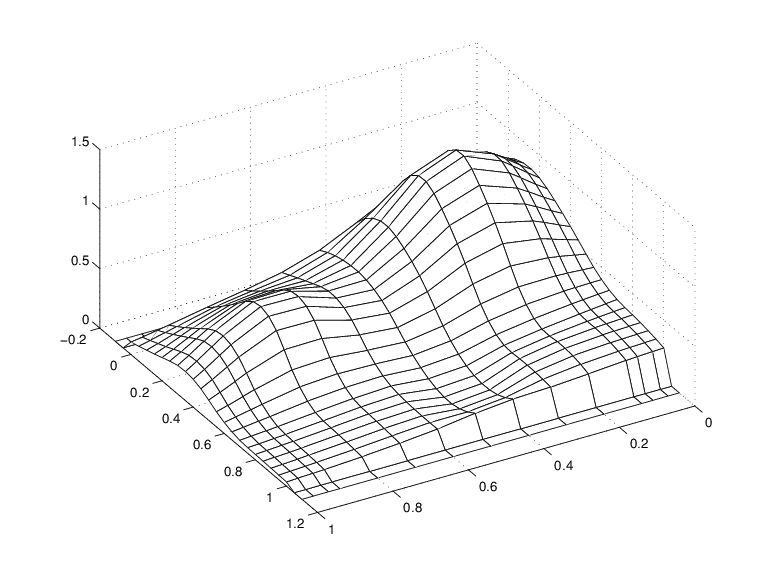
Обратите внимание, что и первые два, и последние два значения на каждой сглаженной кривой на самом деле равны нулю, потому что и первые два, и последние два сайта в yy находятся вне базового интервала для сплайна в sp.
Обратите внимание также на гребни. Они подтверждают, что вы строите графики только в одном направлении.
Чтобы получить фактическую поверхность, вам теперь нужно пройти шаг дальше. Посмотрите на коэффициенты coefsy сплайна в sp:
coefsy = fnbrk(sp,'coefs');
Абстрактно можно думать о сплайне в sp как функцию
с i-й записью coefsy(i,r) коэффициента вектора coefsy(:,r) соответствующий x (i), для всех i. Это предполагает аппроксимацию каждого вектора коэффициентов coefsy(q,:) сплайном того же порядка kx и с той же соответствующей последовательностью узлов knotsx. Без особых причин на этот раз используют кубические сплайны с четырьмя равномерно расположенными внутренними узлами:
kx = 4; knotsx = augknt([0:.2:1],kx); sp2 = spap2(knotsx,kx,x,coefsy.');
Обратите внимание, что spap2(knots,k,x,fx) ожидает fx(:,j) быть опорным элементом в x(j), т.е. ожидает каждый столбец fx быть значением функции. Для соответствия данной величины coefsy(q, :) на x (q), для всех q, настоящее spap2 с транспонированием coefsy.
Теперь рассмотрим транспонирование коэффициентов cxy получившейся сплайн:
coefs = fnbrk(sp2,'coefs').';
Он обеспечивает двухмерный сплайн приближения
к исходным данным
Чтобы построить график поверхности сплайна на сетке, например, сетке
xv = 0:.025:1; yv = 0:.025:1;
Вы можете сделать следующее:
Это приводит к следующему рисунку.
Сплайн Приближения к функции Франке
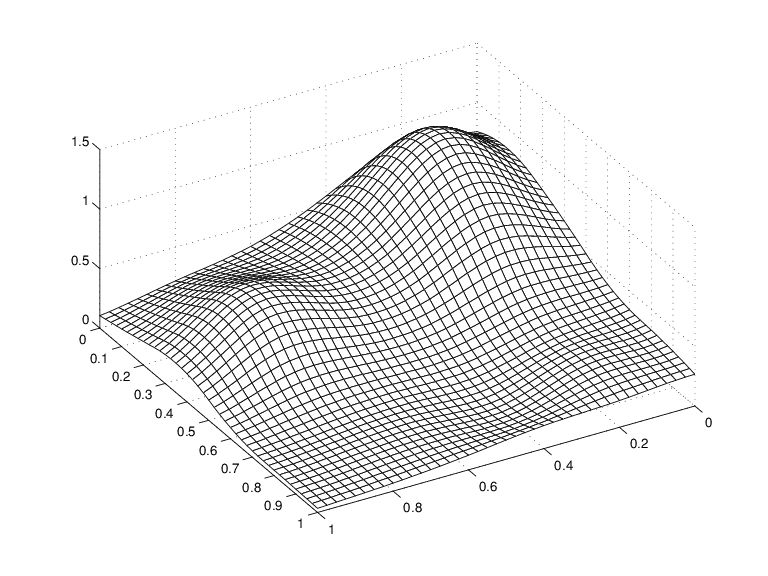
Это имеет хороший смысл, потому что spcol(knotsx,kx,xv) - матрица, чья (i, q) -ая запись равна значению B q, kx (xv (i)) в xv (i) q-го B-сплайна порядка <reservedrangesplaceholder0> для последовательности узлов knotsx.
Потому что матрицы spcol(knotsx,kx,xv) и spcol(knotsy,ky,yv) соединены, это может быть более эффективным, хотя, возможно, более потребляющим память, для больших xv и yv использовать fnval, следующим образом:
value2 = ... fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';
Это, на самом деле, то, что происходит внутри, когда fnval вызывается непосредственно тензорным сплайном продукта, как в
value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});
Вот вычисление относительной погрешностит . е . различия между заданными данными и значением приближения в этих сайтах данных по сравнению с величиной заданных данных:
errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; disp( max(max(abs(errors)))/max(max(abs(z))) )
Выходные выходы 0.0539Возможно, не слишком впечатляюще. Однако массив коэффициентов был только размера 8 6
disp(size(coefs))
для соответствия массиву данных размера 15 11.
disp(size(z))
Применяемый здесь подход кажется предвзятым, следующим образом. Сначала подумайте о заданных данных z как описывающая векторно-оцененную функцию y, а затем обрабатывающая матрицу, образованную векторными коэффициентами аппроксимирующей кривой, как описывающую векторно-оцененную функцию x.
Что происходит, когда вы принимаете вещи в противоположном порядке, то есть думаете о z как описывает векторно-оцененную функцию x, а затем обрабатывает матрицу, составленную из векторных коэффициентов аппроксимирующей кривой, как описывающую векторно-оцененную функцию y?
Возможно, удивительно, что окончательное приближение то же самое, вплоть до округления. Вот численный эксперимент.
Во-первых, подгонка сплайн к данным, но на этот раз с x как независимой переменной, следовательно, это строки z которые теперь становятся значениями данных. Соответственно, вы должны поставить z.', а не z, в spap2,
spb = spap2(knotsx,kx,x,z.');
таким образом получаем сплайн приближения ко всем кривым (x; z (: j)). В частности, оператор
valsb = fnval(spb,xv).';
предоставляет матрицу valsb, чей вход valsb(i, j) может быть принято как приближение к f значений (xv (i), y (j)) базовой функции, f в mesh-точке (xv (i), y (j)). Это очевидно, когда вы строите график valsb использование mesh:
mesh(xv,y,valsb.'), view(150,50)
Другое семейство гладких кривых, притворяющихся поверхностью
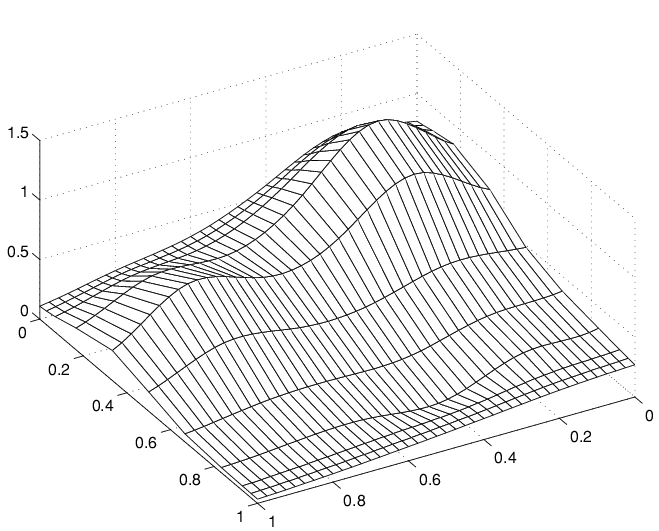
Обратите внимание на гребни. Они подтверждают, что вы, еще раз, строите графики сглаженных кривых только в одном направлении. Но на этот раз кривые бегут в другом направлении.
Теперь наступает второй шаг, чтобы получить фактическую поверхность. Сначала извлеките коэффициенты:
coefsx = fnbrk(spb,'coefs');
Затем подгоняйте каждый вектор коэффициентов coefsx(r,:) сплайном того же порядка ky и с той же соответствующей последовательностью узлов knotsy:
Обратите внимание, что еще раз необходимо транспонировать массив коэффициентов из spb, потому что spap2 принимает столбцы его последнего входного параметра в качестве значений данных.
Соответственно, теперь нет необходимости транспонировать массив коэффициентов coefsb получившейся кривой:
coefsb = fnbrk(spb2,'coefs');
Претензия такова coefsb равен массиву более ранних коэффициентов coefs, вплоть до округления, и вот тест:
disp( max(max(abs(coefs - coefsb))) )
Выходные выходы 1.4433e-15.
Объяснение достаточно простое: Коэффициенты c сплайна s содержащегося в sp = spap2(knots,k,x,y) линейно зависит от входа значений y. Это подразумевает, учитывая, что оба c и y являются матрицами с 1 строкой, что существует некоторая матрица A = A узлов, k x так, что
для любых y данных. Этот оператор выполняется даже тогда, когда y является матрицей, размером d -by- N, скажем, в этом случае каждый опорный y (:, j) принимается точкой в Rd, и полученный сплайн соответственно d -векторно, следовательно, его массив коэффициентов c имеет размер d -by- n, с n = length(knots)-k.
В частности, операторы
sp = spap2(knotsy,ky,y,z); coefsy =fnbrk(sp,'coefs');
предоставьте нам матрицу coefsy который удовлетворяет
Последующие расчеты
sp2 = spap2(knotsx,kx,x,coefsy.'); coefs = fnbrk(sp2,'coefs').';
сгенерировать массив коэффициентов coefs, что, с учетом двух транспозиций, удовлетворяет
Во втором, альтернативном, вычислении, вы сначала вычислили
spb = spap2(knotsx,kx,x,z.'); coefsx = fnbrk(spb,'coefs');
следовательно coefsx= z '.Акноцкс, kx, x. Последующий расчет
spb2 = spap2(knotsy,ky,y,coefsx.'); coefsb = fnbrk(spb,'coefs');
затем предоставлено
Следовательно, coefsb = coefs.
Второй подход более симметричен, чем первый в том, что транспонирование происходит в каждом вызове к spap2 и нигде больше. Этот подход может использоваться для приближения к данным с сеткой в любом количестве переменных.
Если, например, данные по трехмерной сетке содержатся в некотором трехмерном массиве v размера [Nx,Ny,Nz], с v(i,j,k) содержащий f значений (x (i), y (j), z (k)), тогда вы бы начали с
coefs = reshape(v,Nx,Ny*Nz);
Принимая, что nj = knotsj - kj, для j = x,y,zЗатем необходимо выполнить следующие действия:
sp = spap2(knotsx,kx,x,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),Ny,Nz*nx); sp = spap2(knotsy,ky,y,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),Nz,nx*ny); sp = spap2(knotsz,kz,z,coefs.'); coefs = reshape(fnbrk(sp,'coefs'),nx,ny*nz);
См. главу 17 PGS или [C. de Boor, «Эффективная компьютерная манипуляция тензорными продуктами», ACM Trans. Math. Software 5 (1979), 173-182; Исправления, 525] для получения дополнительной информации. Эти же ссылки также дают понять, что здесь нет ничего особенного в использовании приближения методом наименьших квадратов. Любой процесс аппроксимации, включая сплайн интерполяцию, чье результирующее приближение имеет коэффициенты, которые линейно зависят от заданных данных, может быть расширен таким же образом до многомерного процесса аппроксимации к данным с сеткой.
Это именно то, что используется в командах конструкции сплайнов csapi, csape, spapi, spaps, и spap2, при необходимости установки сетчатых данных. Также используется в fnval, когда тензорный сплайн продукта должен быть оценен на сетке.