Тулбокс предоставляет одно- и двух- терминовую экспоненциальную модель, как задано
Экспоненциалов часто используются, когда скорость изменения количества пропорциональна начальной сумме количества. Если коэффициент, сопоставленный с b и/или d, отрицателен, y представляет экспоненциал распад. Если коэффициент положительный, y представляет экспоненциальный рост.
Для примера один режим радиоактивного распада нуклида описывается однократным экспоненциалом. a интерпретируется как начальное количество ядер, b является константой распада, x является временем, и y является количеством оставшихся ядер после определенного времени. Если существуют два режима распада, то необходимо использовать двухсрочную экспоненциальную модель. Для второго режима распада, вы добавляете другой экспоненциальный член к модели.
Примеры экспоненциального роста включают заразные заболевания, при которых лекарство недоступно, и биологические населения, рост которых не сдерживается хищничеством, факторами окружающей среды и так далее.
Откройте приложение Аппроксимирование Кривыми, введя cftool. Также щелкните Аппроксимированием кривыми на вкладке Приложений.
В приложении Аппроксимирование Кривыми выберите данные кривой (X data и Y data, или просто Y data с индексом).
Приложение Аппроксимирование Кривыми создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели из Polynomial на Exponential.
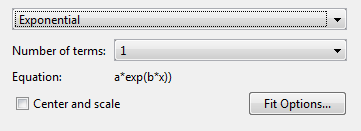
Можно задать следующие опции:
Выберите один или два условия для подгонки exp1 или exp2.
Смотрите на панели Results, чтобы увидеть условия модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Щелкните Fit Options, чтобы задать начальные значения коэффициентов и ограничения, соответствующие вашим данным, или измените настройки алгоритма.
Тулбокс вычисляет оптимизированные начальные точки для экспоненциальных подгонок на основе текущего набора данных. Можно переопределить начальные точки и задать свои собственные значения в диалоговом окне Опции подгонки (Fit Options).
Опции аппроксимации для однократной экспоненциальной показаны далее. Начальные значения коэффициентов и ограничения предназначены для данных переписи.
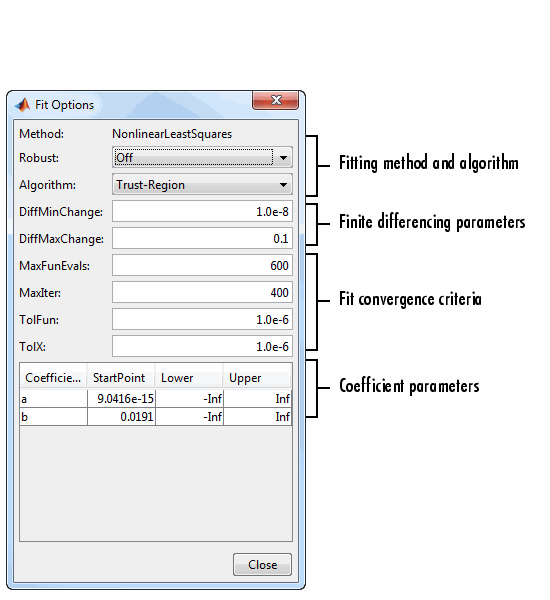
Для примера, задающего стартовые значения, соответствующие данным, смотрите Гауссов подбор кривой с экспоненциальным фоном.
Для получения дополнительной информации о настройках см. Раздел «Задание опций подгонки» и «Оптимизированные начальные точки».
Этот пример показывает аппроксимацию экспоненциальной модели к данным с помощью fit функция.
Экспоненциальная модель библиотеки является входным параметром к fit и fittype функций. Задайте тип модели 'exp1' или 'exp2' .
Подбор однократной экспоненциальной модели
Сгенерируйте данные с экспоненциальным трендом и затем подгоняйте данные с помощью однократного экспоненциального. Постройте график подгонки и данных.
x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.1*randn(size(x));
f = fit(x,y,'exp1')f =
General model Exp1:
f(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 2.021 (1.89, 2.151)
b = -0.1812 (-0.2104, -0.152)
plot(f,x,y)

Подбор двухсрочной экспоненциальной модели
f2 = fit(x,y,'exp2')f2 =
General model Exp2:
f2(x) = a*exp(b*x) + c*exp(d*x)
Coefficients (with 95% confidence bounds):
a = 2443 (-1.229e+12, 1.229e+12)
b = -0.2574 (-1.87e+04, 1.87e+04)
c = -2441 (-1.229e+12, 1.229e+12)
d = -0.2575 (-1.872e+04, 1.872e+04)
plot(f2,x,y)

Задание начальных точек
Тулбокс вычисляет оптимизированные стартовые точки для экспоненциальных подгонок на основе текущего набора данных. Можно переопределить начальные точки и задать свои собственные значения.
Найдите порядок записей для коэффициентов в первой модели (f ) при помощи coeffnames функция.
coeffnames(f)
ans = 2x1 cell
{'a'}
{'b'}
Если вы задаете стартовые точки, выберите значения, соответствующие вашим данным. Установите произвольные начальные точки для коэффициентов a и b в пример целях.
f = fit(x,y,'exp1','StartPoint',[1,2])
f =
General model Exp1:
f(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 2.021 (1.89, 2.151)
b = -0.1812 (-0.2104, -0.152)
plot(f,x,y)

Исследуйте опции экспоненциальной подгонки
Исследуйте опции подгонки, если вы хотите изменить опции подгонки, такие как начальные значения коэффициентов и ограничения, соответствующие вашим данным, или изменить настройки алгоритма. Для получения дополнительной информации об этих опциях смотрите таблицу свойств для NonlinearLastSquares на fitoptions страница с описанием.
fitoptions('exp1')ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Robust: 'Off'
StartPoint: [1x0 double]
Lower: [1x0 double]
Upper: [1x0 double]
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
fit | fitoptions | fittype