Полиномиальные модели для кривых заданы
где n + 1 является порядком полинома, n - степень полинома и 1 ≤ <reservedrangesplaceholder0> ≤ 9. Порядок задает количество коэффициентов, которые будут соответствовать, и степень дает самую высокую степень переменной предиктора.
В этом руководстве полиномы описаны в терминах их степени. Для примера полином третьей степени (кубический) задается как
Полиномы часто используются, когда требуется простая эмпирическая модель. Можно использовать полиномиальную модель для интерполяции или экстраполяции или для характеристики данных с помощью глобальной подгонки. Для примера преобразование температуры в напряжение для термопары типа J в диапазоне от 0 до 760o температурная область значений описана полиномом седьмой степени.
Примечание
Если вы не нуждаетесь в глобальной параметрической подгонке и хотите максимизировать гибкость подгонки, кусочные полиномы могут обеспечить лучший подход. Для получения дополнительной информации см. раздел «Непараметрический подбор кривой».
Основные преимущества аппроксимаций полиномом включают разумную гибкость для данных, которая не слишком сложна, и они линейны, что означает, что процесс подгонки прост. Главный недостаток заключается в том, что подгонки высокой степени могут стать нестабильными. Кроме того, полиномы любой степени могут обеспечить хорошую подгонку в области значений данных, но могут дико различаться вне этой области значений. Поэтому проявляйте осторожность при экстраполяции полиномами.
Когда вы подбираетесь с полиномами высокой степени, процедура аппроксимации использует значения предиктора в качестве базиса для матрицы с очень большими значениями, что может привести к проблемам масштабирования. Чтобы справиться с этим, вы должны нормализовать данные, центрируя их в нулевом среднем и масштабируя их до стандартного отклонения модулей измерения. Нормализуйте данные путем установки флажка Центр и шкалу в приложении Аппроксимирование Кривыми.
Откройте приложение Аппроксимирование Кривыми, введя cftool. Также щелкните Аппроксимированием кривыми на вкладке Приложений.
В приложении Аппроксимирование Кривыми выберите данные кривой или поверхности.
Если вы выбираете данные кривой (X data и Y data, или просто Y data с индексом), приложение Аппроксимирование Кривыми создает подгонку кривой по умолчанию, Polynomial.
Если вы выбираете данные поверхности (X data, Y data и Z data), приложение Аппроксимирование Кривыми создает поверхностную подгонку по умолчанию Interpolant. Измените тип модели из Interpolant на Polynomial.
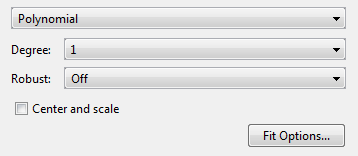
Для кривых, Polynomial модель подходит для полинома в x.
Для поверхностей, Polynomial модель подходит для полинома в x и y.
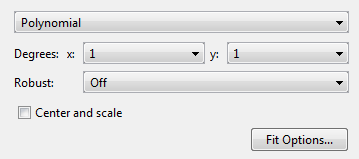
Можно задать следующие опции:
Степень для x и y входов:
Для кривых степень x может быть до 9.
Для поверхностей степень x и y может быть до 5.
Степень полинома является максимальной из x и y степеней. Смотрите Определение Полиномиальных Терминов для Полиномиальных Поверхностных Аппроксимаций.
Устойчивый линейный метод аппроксимации методом наименьших квадратов для использования (Off, LAR, или Bisquare). Для получения дополнительной информации смотрите Robust на fitoptions страница с описанием.
Установите границы или исключить условия нажав Fit Options. Можно исключить любой термин, установив его границы равными 0.
Смотрите на панели Results, чтобы увидеть условия модели, значения коэффициентов и статистику качества подгонки.
Совет
Если переменные входы имеют очень разные шкалы, установите и снимите флажок Center and scale, чтобы увидеть различие в подгонке. Сообщения на панели Results подсказывают, что масштабирование может улучшить вашу подгонку.
Для примера сравнения различных аппроксимаций полиномом см. «Сравнение подгонок в приложении Аппроксимирование Кривыми».
В этом примере показано, как использовать fit функция для аппроксимации полиномов к данным. Шаги строятся и строят полиномы кривых и поверхности, задают опции подгонки, возвращают качество статистики подгонки, вычисляют предсказания и показывают доверительные интервалы.
Модель полиномиальной библиотеки является входным параметром к функциям подгонки и fittype. Задайте тип модели poly далее следует степень x (до 9), или x и y (до 5). Для примера задаете квадратичную кривую с 'poly2' , или кубическая поверхность с 'poly33' .
Создайте и постройте квадратичную полиномиальную кривую
Загрузите некоторые данные и подгоните квадратичный полином. Задайте квадратичный, или полином второй степени, с помощью строки 'poly2' .
load census; fitpoly2=fit(cdate,pop,'poly2') % Plot the fit with the plot method. plot(fitpoly2,cdate,pop) % Move the legend to the top left corner. legend('Location','NorthWest' );
fitpoly2 =
Linear model Poly2:
fitpoly2(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)

Создание кубической кривой
Аппроксимация кубического полинома 'poly3'.
fitpoly3=fit(cdate,pop,'poly3')
plot(fitpoly3,cdate,pop)
Warning: Equation is badly conditioned. Remove repeated data points or try
centering and scaling.
fitpoly3 =
Linear model Poly3:
fitpoly3(x) = p1*x^3 + p2*x^2 + p3*x + p4
Coefficients (with 95% confidence bounds):
p1 = 3.855e-06 (-4.078e-06, 1.179e-05)
p2 = -0.01532 (-0.06031, 0.02967)
p3 = 17.78 (-67.2, 102.8)
p4 = -4852 (-5.834e+04, 4.863e+04)

Настройка опций подгонки
Кубическое соответствие предупреждает, что уравнение плохо обусловлено, поэтому вы должны попробовать центрирование и масштабирование, задав 'Normalize' опция. Подгонка кубического полинома с помощью опций как центра, так и шкалы и устойчивой подгонки. Устойчивые 'on' - ярлык, эквивалентный 'Bisquare' , метод по умолчанию для устойчивого линейного метода аппроксимации методом наименьших квадратов.
fit3=fit(cdate, pop,'poly3','Normalize','on','Robust','on') plot(fit3,cdate,pop)
fit3 =
Linear model Poly3:
fit3(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = -0.4619 (-1.895, 0.9707)
p2 = 25.01 (23.79, 26.22)
p3 = 77.03 (74.37, 79.7)
p4 = 62.81 (61.26, 64.37)

Чтобы узнать, какие параметры можно задать для модели библиотеки 'poly3' , используйте функцию fitoptions.
fitoptions poly3
ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'LinearLeastSquares'
Robust: 'Off'
Lower: [1x0 double]
Upper: [1x0 double]
Получите качество подгонки статистики
Задайте 'gof' выходной аргумент для получения статистики качества подгонки для кубической аппроксимации полиномом.
[fit4, gof]=fit(cdate, pop,'poly3','Normalize','on'); gof
gof =
struct with fields:
sse: 149.7687
rsquare: 0.9988
dfe: 17
adjrsquare: 0.9986
rmse: 2.9682
Постройте график невязок для оценки подгонки
Чтобы построить графики невязок, задайте 'residuals' как тип графика в методе plot.
plot(fit4,cdate, pop,'residuals');

Исследуйте подгонку за пределы области значений данных
По умолчанию подгонка строится в области значений данных. Чтобы построить график подгонки в другой области значений, установите пределы X осей перед построением графика подгонки. Для примера, чтобы увидеть значения, экстраполированные из подгонки, установите верхний предел X равный 2050.
plot( cdate, pop, 'o' ); xlim( [1900, 2050] ); hold on plot( fit4 ); hold off

Постройте границы предсказания
Чтобы построить графики границ предсказания, используйте 'predobs' или 'predfun' как тип графика.
plot(fit4,cdate,pop,'predobs')

Постройте графики границ предсказания для кубического полинома до 2050 года.
plot( cdate, pop, 'o' ); xlim( [1900, 2050] ) hold on plot( fit4, 'predobs' ); hold off

Получите доверительные границы в новых точках запроса
Рассчитать подгонку для некоторых новых точек запроса.
cdateFuture = (2000:10:2020).'; popFuture = fit4( cdateFuture )
popFuture = 276.9632 305.4420 335.5066
Вычислите 95% доверия ограничения на предсказание для населения в будущем, используя метод predint.
ci = predint( fit4, cdateFuture, 0.95, 'observation' )
ci = 267.8589 286.0674 294.3070 316.5770 321.5924 349.4208
Постройте график предсказанного будущего населения с доверительными интервалами относительно подгонки и данных.
plot(cdate, pop, 'o'); xlim([1900, 2040]) hold on plot(fit4) h = errorbar(cdateFuture,popFuture,popFuture-ci(:,1),ci(:,2)-popFuture,'.'); hold off legend('cdate v pop','poly3','prediction','Location','NorthWest')

Построение и построение графика полиномиальной поверхности
Загрузите некоторые данные поверхности и подгоните полином четвертой степени в x и y.
load franke; fitsurface=fit([x,y],z, 'poly44','Normalize','on') plot(fitsurface, [x,y],z)
Linear model Poly44:
fitsurface(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3
+ p21*x^2*y + p12*x*y^2 + p03*y^3 + p40*x^4 + p31*x^3*y
+ p22*x^2*y^2 + p13*x*y^3 + p04*y^4
where x is normalized by mean 1982 and std 868.6
and where y is normalized by mean 0.4972 and std 0.2897
Coefficients (with 95% confidence bounds):
p00 = 0.3471 (0.3033, 0.3909)
p10 = -0.1502 (-0.1935, -0.107)
p01 = -0.4203 (-0.4637, -0.377)
p20 = 0.2165 (0.1514, 0.2815)
p11 = 0.1717 (0.1175, 0.2259)
p02 = 0.03189 (-0.03351, 0.09729)
p30 = 0.02778 (0.00749, 0.04806)
p21 = 0.01501 (-0.002807, 0.03283)
p12 = -0.03659 (-0.05439, -0.01879)
p03 = 0.1184 (0.09812, 0.1387)
p40 = -0.07661 (-0.09984, -0.05338)
p31 = -0.02487 (-0.04512, -0.004624)
p22 = 0.0007464 (-0.01948, 0.02098)
p13 = -0.02962 (-0.04987, -0.009366)
p04 = -0.02399 (-0.0474, -0.0005797)

Все методы аппроксимации имеют свойства по умолчанию Normalize, Exclude, Weights, и Method. Для получения примера смотрите Определение Опций подгонки в командной строке.
Полиномиальные модели имеют Method значение свойства LinearLeastSquares, и дополнительные свойства опций подгонки, показанные в следующей таблице. Для получения дополнительной информации обо всех опциях подгонки, смотрите fitoptions страница с описанием.
Свойство | Описание |
|---|---|
| Задает устойчивый линейный метод аппроксимации методом наименьших квадратов для использования. Значения |
| Вектор с нижними границами коэффициентов, которые будут установлены. Значение по умолчанию является пустым вектором, что указывает на то, что подгонка не ограничена нижними границами. Если ограничения заданы, длина вектора должна равняться количеству коэффициентов. Отдельные без ограничений нижние границы могут быть заданы |
| Вектор верхних границ коэффициентов, которые будут установлены. Значение по умолчанию является пустым вектором, что указывает на то, что подгонка не ограничена верхними границами. Если ограничения заданы, длина вектора должна равняться количеству коэффициентов. Отдельные без ограничений верхние границы могут задаваться |
Можно управлять терминами для включения в модель полиномиальной поверхности, задавая степени для входов x и y. Если i - степень в x, а j - степень в y, общая степень полинома является максимальной из i и j. Степень x в каждом члене меньше или равна i, и степень y в каждом члене меньше или равна j. Максимум и для i, и для j - пять.
Для примера:
poly21 Z = p00 + p10*x + p01*y + p20*x^2 + p11*x*y
poly13 Z = p00 + p10*x + p01*y + p11*x*y + p02*y^2
+ p12*x*y^2 + p03*y^3poly55 Z = p00 + p10*x + p01*y +...+ p14*x*y^4
+ p05*y^5Для примера, если вы задаете степень x 3 и степень y 2, имя модели poly32. Условия модели следуют форме в этой таблице.
| Степень срочности | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | y | y2 |
| 1 | x | xy | xy2 |
| 2 | x2 | x2y | Н/Д |
| 3 | x3 | Н/Д | Н/Д |
Общая степень полинома не может превышать максимума в i и j. В этом примере такие термины, как x3y и x2y2 исключены, потому что их степени равны более 3. В обоих случаях общая степень 4.
fit | fitoptions | fittype | Имена полиномиальных моделей и уравнения