Рациональные модели заданы как отношения полиномов и заданы
где n - степень полинома нумератора и 0 ≤ <reservedrangesplaceholder2> ≤ 5, в то время как m - степень полинома знаменателя и 1 ≤ <reservedrangesplaceholder0> ≤ 5. Обратите внимание, что коэффициент, сопоставленный с xm всегда равен 1. Это делает числитель и знаменатель уникальными, когда полиномиальные степени одинаковы.
В этом руководстве рационалы описаны в терминах степени числителя/степени знаменателя. Для примера квадратичное/кубическое рациональное уравнение задается как
Как и полиномы, рациональы часто используются, когда требуется простая эмпирическая модель. Основным преимуществом рациональных методов является их гибкость с данными, которые имеют сложную структуру. Главный недостаток состоит в том, что они становятся нестабильными, когда знаменатель находится около 0. Для примера, который использует рациональные полиномы различных степеней, смотрите Пример: Рациональная подгонка.
Откройте приложение Аппроксимирование Кривыми, введя cftool. Также щелкните Аппроксимированием кривыми на вкладке Приложений.
В приложении Аппроксимирование Кривыми выберите данные кривой (X data и Y data, или просто Y data с индексом).
Приложение Аппроксимирование Кривыми создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели из Polynomial на Rational.
Можно задать следующие опции:
Выберите степень числителя и полиномов знаменателя. Числитель может иметь степень 0 на 5, и знаменатель от 1 на 5.
Смотрите на панели Results, чтобы увидеть условия модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Щелкните Fit Options, чтобы задать начальные значения коэффициентов и ограничения или изменить настройки алгоритма.
Тулбокс вычисляет случайные начальные точки для рациональных моделей, заданные на интервале [0,1]. Можно переопределить начальные точки и задать свои собственные значения в диалоговом окне Опции подгонки (Fit Options).
Для получения дополнительной информации о настройках см. Раздел «Задание опций подгонки» и «Оптимизированные начальные точки».
Задайте тип модели ratij, где i - степень полинома числителя, а j - степень полинома знаменателя. Для примера, 'rat02', 'rat21' или 'rat55'.
Для примера, чтобы загрузить некоторые данные и соответствовать рациональной модели:
load hahn1; f = fit( temp, thermex, 'rat32') plot(f,temp,thermex)
См. Пример: Рациональная подгонка, чтобы соответствовать этому примеру в интерактивном режиме с различными рациональными моделями.
Если вы хотите изменить опции подгонки, такие как начальные значения коэффициентов и ограничения, соответствующие вашим данным, или изменить настройки алгоритма, смотрите таблицу дополнительных свойств с NonlinearLeastSquares на fitoptions страница с описанием.
Этот пример подходит для измеренных данных с помощью рациональной модели. Данные описывают коэффициент теплового расширения для меди как функцию от температуры в степенях кельвина.
Для этого набора данных вы найдете рациональное уравнение, которое производит лучшую подгонку. Рациональные модели заданы как отношение полиномов как заданное:
где n - степень полинома числителя, а m - степень многочлена знаменателя. Обратите внимание, что рациональные уравнения не связаны с физическими параметрами данных. Вместо этого они обеспечивают простую и гибкую эмпирическую модель, которую вы можете использовать для интерполяции и экстраполяции.
Загрузите данные теплового расширения из файла hahn1.mat, который поставляется с тулбоксом.
load hahn1
Рабочая область содержит две новые переменные:
temp - вектор температур в степенях кельвина.
thermex является вектором коэффициентов теплового расширения для меди.
Откройте приложение Аппроксимирование Кривыми, введя:
cftool
Выберите temp и thermex из X data и Y data списков.
Приложение Аппроксимирование Кривыми подходит и строит графики данных.
Выберите Rational в списке категорий подгонки.
Попробуйте начальный выбор для рациональной модели квадратичного/квадратичного. Выберите 2как для Numerator degree, так и для Denominator degree.

Приложение Аппроксимирование Кривыми подходит для квадратичного/квадратичного рационального.
Исследуйте невязки. Выберите View > Residuals Plot или нажмите кнопку на панели инструментов.
Исследуйте данные, подгонку и невязки. Заметьте, что подгонка пропускает данные для наименьших и самых больших значений предиктора. Кроме того, невязки показывают сильный шаблон во всем наборе данных, что указывает на то, что возможна лучшая подгонка.

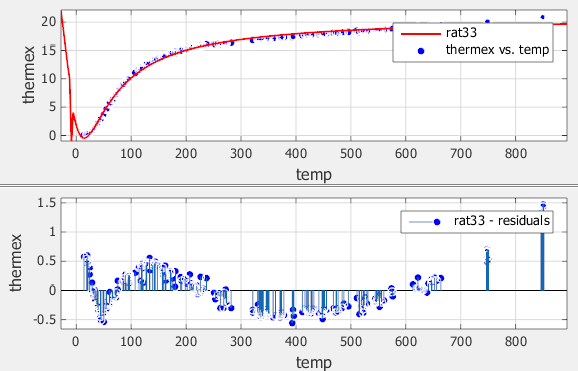
Для следующей подгонки попробуйте кубическое/кубическое уравнение. Выберите 3как для Numerator degree, так и для Denominator degree.
Исследуйте данные, подгонку и невязки. Подгонка показывает несколько разрывов вокруг нулей знаменателя.
Примечание
Ваши результаты зависят от случайных начальных точек и могут отличаться от показанных.
Посмотрите на Results панели. Сообщение и числовые результаты указывают, что подгонка не сходилась.
Fit computation did not converge: Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum.
Несмотря на то, что сообщение на панели Результаты указывает, что вы можете улучшить подгонку, если вы увеличите максимальное количество итераций, лучший выбор на этом этапе процесса подгонки состоит в том, чтобы использовать другое рациональное уравнение, потому что подгонка тока содержит несколько разрывов. Эти разрывы обусловлены взрывом функции при значениях предиктора, которые соответствуют нулям знаменателя.
Попробуйте подгонять данные с помощью кубического/квадратичного уравнения. Выберите 2 для Denominator degree и оставьте набор Numerator degree равным 3.
Входные переменные имеют очень разные шкалы, поэтому выберите опцию Center and scale.
Данные, подгонка и невязки показаны ниже.

Подгонка хорошо себя ведет во всей области значений данных, и невязки случайным образом рассеиваются около нуля. Поэтому можно уверенно использовать эту подгонку для последующего анализа.
fit | fitoptions | fittype