stmak

Соберите функцию в stform

Синтаксис

stmak(centers,coefs) st = stmak(centers,x,type) st = stmak(centers,coefs,type,interv)

Описание

stmak(centers,coefs) возвращает stform функции, f задается как

$f (x) = \sum_{j = 1}^{n} coefs (:, j) \cdot ψ (x - центры (:, j))$

$ψ (x) = {| x |}^{2} \log {| x |}^{2}$

тонкопластинчатый сплайн базиса функции и со |<reservedrangesplaceholder1>|, обозначающими евклидову норму вектора x.

centers и coefs должны быть матрицами с одинаковым числом столбцов.

st = stmak(centers,x,type) магазины в st stform функции f заданная как

$f (x) = \sum_{j = 1}^{n} coefs (:, j) \cdot ψ_{j} (x)$

с ψ j как обозначено вектором символов type, который может быть одним из следующих:

'tp00', для тонкопластинчатого сплайна;
'tp10'для первой производной тонкопластинчатого сплайна относительно его первого аргумента;
'tp01'для первой производной тонкопластинчатого сплайна относительно его второго аргумента;
'tp', значение по умолчанию.

Вот подробности.

`'tp00'`	ψ j (x) = и (\|<reservedrangesplaceholder2> - c j \|²), _{<reservedrangesplaceholder1> <reservedrangesplaceholder0>} with (t) = t журнал (t) <reservedrangesplaceholder3> <reservedrangesplaceholder2>-2 (<reservedrangesplaceholder1>) = x (1) <reservedrangesplaceholder3> <reservedrangesplaceholder2>-1 (<reservedrangesplaceholder1>) = x (2) <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>) = 1
`'tp10'`	ψ j (x) = и (\|<reservedrangesplaceholder2> - c j \|²), _{<reservedrangesplaceholder1> <reservedrangesplaceholder0>} с φ (<reservedrangesplaceholder11>) = (D 1 t) (журнал t + 1), и <reservedrangesplaceholder7> 1 <reservedrangesplaceholder6> частная производная t = t (<reservedrangesplaceholder3>) = \| x - <reservedrangesplaceholder1> <reservedrangesplaceholder0> \|² по отношению к x (1) <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>) = 1
`'tp01'`	ψ j (x) = и (\|<reservedrangesplaceholder2> - c j \|²), _{<reservedrangesplaceholder1> <reservedrangesplaceholder0>} с φ (<reservedrangesplaceholder11>) = (D 2 t) (журнал t + 1), и <reservedrangesplaceholder7> 2 <reservedrangesplaceholder6> частная производная t = t (<reservedrangesplaceholder3>) = \| x - <reservedrangesplaceholder1> <reservedrangesplaceholder0> \|² по отношению к x (2) <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>) = 1
`'tp'` (по умолчанию)	ψ j (x) = и (\|<reservedrangesplaceholder2> - c j \|²), _{<reservedrangesplaceholder1> <reservedrangesplaceholder0>} with (t) = t журнал (t)

st = stmak(centers,coefs,type,interv) также задает основной интервал для формы, с interv{j} указание, в форме [a,b], область значений jth переменная. Значение по умолчанию для interv является наименьшей такой коробкой, которая содержит все заданные центры.

Примеры

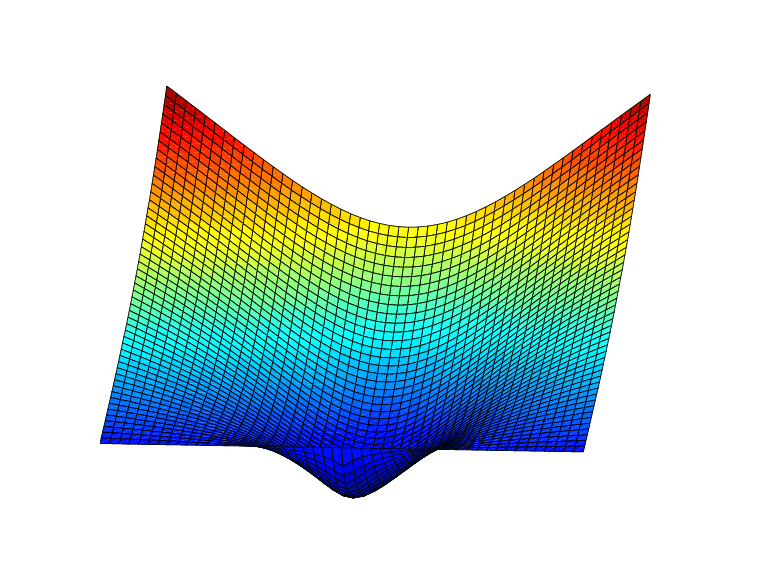
Пример 1. Следующее генерирует рисунок ниже, функции базиса тонкопластинчатых сплайнов, $ψ (x) = {| x |}^{2} \log {| x |}^{2},$ но подходящим образом ограничено, чтобы показать, что эта функция отрицательна около источника. Для этого есть дополнительные линии, чтобы указать нулевой уровень.

inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],1),{inx,iny})
hold on, plot(inx,repmat(linspace(iny(1),iny(2),11),2,1),'r')
view([25,20]),axis off, hold off

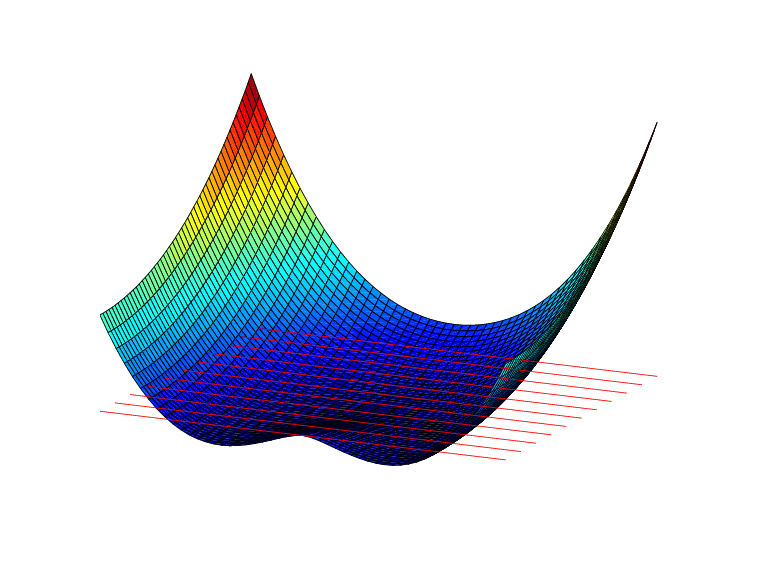
Пример 2. Теперь мы также генерируем и строим на графике, в той же самой области, первую частную производную D 2 ψ функции тонкопластинчатого сплайн-базиса относительно его второго аргумента.

inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],[1 0],'tp01',{inx,iny}))
view([13,10]),shading flat,axis off

Обратите внимание, что на этот раз мы явным образом установили основной интервал для stform.

Полученный рисунок ниже показывает очень сильное изменение около источника. Это отражает тот факт, что вторые производные ψ имеют там логарифмическую особенность.

См. также

stcol

Документация по Curve Fitting Toolbox

Поддержка

Сообщество Экспонента