Сумма модели синусов соответствует периодическим функциям и дается
где a - амплитуда, b - частота, а c - фаза константа для каждого члена синусоиды. n - количество членов в ряду и 1 ≤ n ≤ 8. Это уравнение тесно связано с серией Фурье, описанной в серии Фурье. Основным отличием является то, что сумма уравнений синусов включает в себя фазовую константу и не включает в себя постоянный (перехват) член.
Откройте приложение Аппроксимирование Кривыми, введя cftool. Также щелкните Аппроксимированием кривыми на вкладке Приложений.
В приложении Аппроксимирование Кривыми выберите данные кривой (X data и Y data, или просто Y data с индексом).
Приложение Аппроксимирование Кривыми создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели из Polynomial на Sum of Sine.
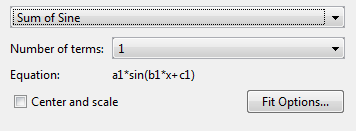
Можно задать следующие опции:
Выберите количество терминов: 1 на 8.
Смотрите на панели Results, чтобы увидеть условия модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Щелкните Fit Options, чтобы задать начальные значения коэффициентов и ограничения или изменить настройки алгоритма.
Тулбокс вычисляет оптимизированные начальные точки для суммы синусоидальных моделей на основе текущего набора данных. Можно переопределить начальные точки и задать свои собственные значения в диалоговом окне Опции подгонки (Fit Options).
Сумма синусоидальной модели имеет нижнее ограничение на c i 0. Нижние границы по умолчанию для большинства библиотечных моделей -Inf.
Для получения дополнительной информации о настройках см. Раздел «Задание опций подгонки» и «Оптимизированные начальные точки».
Задайте тип модели sin далее указывается количество терминов, например 'sin1' на 'sin8'.
Для примера, чтобы загрузить некоторые периодические данные и подогнать шестизначную сумму синусоидальной модели:
load enso; f = fit( month, pressure, 'sin6') plot(f,month,pressure)
Если вы хотите изменить опции подгонки, такие как начальные значения коэффициентов и ограничения, соответствующие вашим данным, или изменить настройки алгоритма, смотрите таблицу дополнительных свойств с NonlinearLeastSquares на fitoptions страница с описанием.
fit | fitoptions | fittype