Совет
Чтобы узнать, как настроить параметры для нейронной сети для глубокого обучения, смотрите Настройте Параметры и Обучите Сверточную Нейронную Сеть.
Одна из проблем, которая возникает во время обучения нейронной сети, называется избыточным обучением. Ошибка на наборе обучающих данных доводится до очень небольшого значения, но при представлении новых данных в сеть ошибка велика. Сеть запомнила обучающие примеры, но не научилась обобщать на новые ситуации.
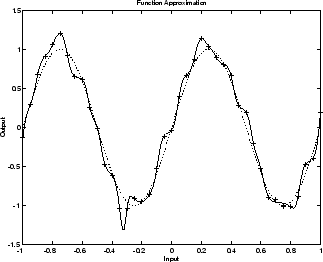
Следующий рисунок показывает реакцию нейронной сети 1-20-1, которая была обучена аппроксимировать шумную функцию синуса. Базовая функция синуса показана пунктирной линией, шумные измерения заданы символами +, а реакция нейронной сети задается сплошной линией. Очевидно, что эта сеть переоборудовала данные и не будет хорошо обобщаться.
Одним из методов улучшения обобщения сети является использование сети, которая просто является достаточно большой, чтобы обеспечить адекватную подгонку. Чем больше сеть вы используете, тем сложнее функции может создать сеть. Если вы используете достаточно маленькую сеть, ей не хватит степени, чтобы перегружать данные. Запустите
пример Neural Network Design nnd11gn [HDB96], чтобы выяснить, как уменьшение размера сети может предотвратить сверхподбор кривой.
К сожалению, заранее трудно узнать, насколько велика должна быть сеть для конкретного приложения. Существует два других метода улучшения обобщения, которые реализованы в программном обеспечении Deep Learning Toolbox™: регуляризация и ранняя остановка. В следующих разделах описываются эти два метода и стандартные программы их реализации.
Обратите внимание, что если количество параметров в сети намного меньше, чем общее число точек в набор обучающих данных, то шансов на сверхподбор кривой мало или его нет. Если можно легко собрать больше данных и увеличить размер набора обучающих данных, то не стоит беспокоиться о следующих методах предотвращения сверхподбора кривой. Остальная часть этого раздела относится только к тем ситуациям, в которых вы хотите максимально использовать ограниченный объем данных.
Обычно каждый сеанс обучения по обратному распространению начинается с различных начальных весов и смещений, а различные деления данных - с обучения, валидации и тестовых наборов. Эти различные условия могут привести к очень разным решениям одной и той же задачи.
Это хорошая идея, чтобы обучить несколько сетей, чтобы гарантировать, что сеть с хорошим обобщением найдена.
Здесь загружается набор данных, разделенный на две части: 90% для проектирования сетей и 10% для проверки всех.
[x, t] = bodyfat_dataset; Q = size(x, 2); Q1 = floor(Q * 0.90); Q2 = Q - Q1; ind = randperm(Q); ind1 = ind(1:Q1); ind2 = ind(Q1 + (1:Q2)); x1 = x(:, ind1); t1 = t(:, ind1); x2 = x(:, ind2); t2 = t(:, ind2);
Затем сетевую архитектуру выбирают и обучают десять раз на первой части набора данных со средней квадратной ошибкой каждой сети на второй части набора данных.
net = feedforwardnet(10);
numNN = 10;
NN = cell(1, numNN);
perfs = zeros(1, numNN);
for i = 1:numNN
fprintf('Training %d/%d\n', i, numNN);
NN{i} = train(net, x1, t1);
y2 = NN{i}(x2);
perfs(i) = mse(net, t2, y2);
endКаждая сеть будет обучаться, начиная с различных начальных весов и смещений, и с различным делением первого набора данных на наборы для обучения, валидации и тестирования. Обратите внимание, что тестовые наборы являются хорошей мерой обобщения для каждой соответствующей сети, но не для всех сетей, потому что данные, которые являются тестовым набором для одной сети, вероятно, будут использоваться для обучения или валидации другими нейронными сетями. Вот почему исходный набор данных был разделен на две части, чтобы гарантировать сохранение полностью независимого тестового набора.
Нейронная сеть с самой низкой эффективностью является той, которая обобщена лучше всего ко второй части набора данных.
Другой простой способ улучшить обобщение, особенно когда это вызвано зашумленными данными или небольшим набором данных, - это обучить несколько нейронных сетей и усреднить их выходы.
Например, здесь 10 нейронных сетей обучаются малой задаче и их средние квадратичные невязки по сравнению со средними квадратичными невязками их среднего значения.
Во-первых, набор данных загружается и разделяется на проект и тестовый набор.
[x, t] = bodyfat_dataset; Q = size(x, 2); Q1 = floor(Q * 0.90); Q2 = Q - Q1; ind = randperm(Q); ind1 = ind(1:Q1); ind2 = ind(Q1 + (1:Q2)); x1 = x(:, ind1); t1 = t(:, ind1); x2 = x(:, ind2); t2 = t(:, ind2);
Затем обучаются десять нейронных сетей.
net = feedforwardnet(10);
numNN = 10;
nets = cell(1, numNN);
for i = 1:numNN
fprintf('Training %d/%d\n', i, numNN)
nets{i} = train(net, x1, t1);
endЗатем каждая сеть тестируется на втором наборе данных с индивидуальными характеристиками и эффективностью для вычисленного среднего выхода.
perfs = zeros(1, numNN);
y2Total = 0;
for i = 1:numNN
neti = nets{i};
y2 = neti(x2);
perfs(i) = mse(neti, t2, y2);
y2Total = y2Total + y2;
end
perfs
y2AverageOutput = y2Total / numNN;
perfAveragedOutputs = mse(nets{1}, t2, y2AverageOutput) Средняя квадратичная невязка для среднего выхода, вероятно, будет ниже, чем большинство отдельных показателей, возможно, не все. Вероятно, он лучше обобщится к дополнительным новым данным.
Для некоторых очень сложных проблем может быть обучена сотня сетей и среднее значение их выходов для любого входа. Это особенно полезно для небольшого, шумного набора данных в сочетании с функцией обучения Регуляризации Байеса trainbr, описанная ниже.
Метод по умолчанию для улучшения обобщения называется ранним остановом. Этот метод автоматически предоставляется для всех контролируемых функций создания сети, включая функции создания сети обратного распространения, такие как feedforwardnet.
В этом методе доступные данные разделяются на три подмножества. Первым подмножеством является набор обучающих данных, который используется для вычисления градиента и обновления весов и смещений сети. Вторым подмножеством является набор валидации. Ошибка на наборе валидации отслеживается в процессе обучения. Ошибка валидации обычно уменьшается на начальной фазе обучения, как и ошибка набора обучающих данных. Однако, когда сеть начинает перегружать данные, ошибка на наборе валидации обычно начинает расти. Когда ошибка валидации увеличивается для заданного количества итераций (net.trainParam.max_fail), обучение останавливается, и возвращаются веса и смещения, минимальные по ошибке валидации.
Ошибка тестового набора не используется во время обучения, но используется для сравнения различных моделей. Также полезно построить график ошибки тестового набора в процессе обучения. Если ошибка в тестовом наборе достигает минимума при значительно отличном количестве итерации от ошибки набора валидации, это может указывать на плохое деление набора данных.
Предусмотрены четыре функции для деления данных на наборы для обучения, валидации и тестирования. Они есть dividerand (по умолчанию), divideblock, divideint, и divideind. Вы можете получить доступ или изменить функцию деления для вашей сети с помощью этого свойства:
net.divideFcn
Каждая из этих функций принимает параметры, которые настраивают ее поведение. Эти значения хранятся и могут быть изменены со следующим свойством сети:
net.divideParam
Создайте простую задачу тестирования. Для полного набора данных сгенерируйте шумную синусоиду с 201 входными точками в диапазоне от − 1 до 1 на шагах 0,01:
p = [-1:0.01:1]; t = sin(2*pi*p)+0.1*randn(size(p));
Разделите данные по индексу, чтобы последовательные выборки назначались набору обучающих данных, набору валидации и тестовому набору последовательно:
trainInd = 1:3:201 valInd = 2:3:201; testInd = 3:3:201; [trainP,valP,testP] = divideind(p,trainInd,valInd,testInd); [trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);
Можно случайным образом разделить входные данные так, чтобы 60% выборок были назначены набором обучающих данных, 20% - набору валидации и 20% - тестовому набору, следующим образом:
[trainP,valP,testP,trainInd,valInd,testInd] = dividerand(p);
Эта функция не только делит входные данные, но и возвращает индексы, так что вы можете разделить целевые данные соответственно используя divideind:
[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);
Можно также разделить входные данные случайным образом, чтобы первые 60% выборок были назначены набором обучающих данных, следующие 20% - набору валидации и последние 20% - тестовому набору, следующим образом:
[trainP,valP,testP,trainInd,valInd,testInd] = divideblock(p);
Разделите целевые данные соответственно с помощью divideind:
[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);
Другой способ разделения входных данных - это циклический цикл выборок между набором обучающих данных, набором валидации и тестовым набором в соответствии с процентами. Можно чередовать 60% выборок с набором обучающих данных, 20% с набором валидации и 20% с тестовым набором следующим образом:
[trainP,valP,testP,trainInd,valInd,testInd] = divideint(p);
Разделите целевые данные соответственно с помощью divideind.
[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);
Другой метод улучшения обобщения называется регуляризацией. Это включает изменение функции эффективности, которая обычно выбирается как сумма квадратов сетевых ошибок на наборе обучающих данных. В следующем разделе объясняется, как можно изменить функцию эффективности, и в следующем разделе описывается стандартная программа, которая автоматически устанавливает оптимальную функцию эффективности, чтобы достичь наилучшего обобщения.
Типичная функция эффективности, используемая для настройки нейронных сетей с feedforward, является средней суммой квадратов сетевых ошибок.
Возможно улучшить обобщение, если вы измените функцию эффективности, добавив термин, который состоит из средней суммы квадратов весов и смещений сети , где - коэффициент эффективности, и
Использование этой функции эффективности заставляет сеть иметь меньшие веса и смещения, и это заставляет сетевой ответ быть более плавным и с меньшей вероятностью избыточным.
Следующий код повторно инициализирует предыдущую сеть и переобучает ее с помощью алгоритма BFGS с регуляризованной функцией эффективности. Здесь коэффициент эффективности установлен на 0,5, что дает равный вес средним квадратным ошибкам и средним квадратным весам.
[x,t] = simplefit_dataset; net = feedforwardnet(10,'trainbfg'); net.divideFcn = ''; net.trainParam.epochs = 300; net.trainParam.goal = 1e-5; net.performParam.regularization = 0.5; net = train(net,x,t);
Проблема регуляризации состоит в том, что трудно определить оптимальное значение для параметра коэффициента эффективности. Если вы сделаете этот параметр слишком большим, вы можете получить сверхподбор кривой. Если коэффициент слишком мал, сеть неадекватно соответствует обучающим данным. В следующем разделе описывается стандартная программа, которая автоматически устанавливает параметры регуляризации.
Желательно определить оптимальные параметры регуляризации автоматическим способом. Одним из подходов к этому процессу является байесовская среда Дэвида Маккея [MacK92]. В этой среда веса и смещения сети приняты как случайные переменные с заданными распределениями. Параметры регуляризации связаны с неизвестными отклонениями, связанными с этими распределениями. Затем можно оценить эти параметры с помощью статистических методов.
Подробное обсуждение байесовской регуляризации выходит за рамки возможностей этого руководства пользователя. Подробное обсуждение использования байесовской регуляризации в сочетании с обучением Левенберга-Марквардта можно найти в [FoHa97].
Байесовская регуляризация была реализована в функции trainbr. Следующий код показывает, как можно обучить сеть 1-20-1 с помощью этой функции, чтобы аппроксимировать шумную синусоиду, показанную на рисунке в Улучшении Обобщения Неглубокой Нейронной Сети и Избегайте Избыточной Подгонки. (Разделение данных отменяется путем установки net.divideFcn так, чтобы эффекты trainbr изолированы от ранней остановки.)
x = -1:0.05:1; t = sin(2*pi*x) + 0.1*randn(size(x)); net = feedforwardnet(20,'trainbr'); net = train(net,x,t);
Одной из функций этого алгоритма является то, что он предоставляет меру того, сколько сетевых параметров (веса и смещения) эффективно используются сетью. В этом случае конечная обученная сеть использует приблизительно 12 параметров (обозначенных #Par в распечатке) из 61 общих весов и смещений в 1-20-1 сети. Это эффективное количество параметров должно оставаться примерно неизменным, независимо от того, насколько большим становится количество параметров в сети. (Это предполагает, что сеть была обучена достаточному количеству итераций для обеспечения сходимости.)
trainbr алгоритм обычно работает лучше всего, когда входы и цели сети масштабируются так, что они падают приблизительно в области значений [− 1,1]. Так обстоит дело с тестовой проблемой здесь. Если ваши входы и цели не попадают в эту область значений, можно использовать функциюmapminmax или mapstd для выполнения масштабирования, как описано в Choose Neural Network Input-Output Processing Functions. Сети, созданные с feedforwardnet включать mapminmax как функцию входа и выхода обработки по умолчанию.
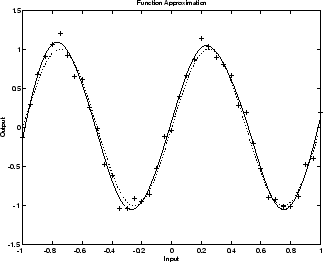
Следующий рисунок показывает ответ обученной сети. В отличие от предыдущего рисунка, на котором сеть 1-20-1 перегружает данные, здесь вы видите, что реакция сети очень близка к базовой функции синуса (пунктирная линия), и, следовательно, сеть хорошо обобщает новые входы. Можно было попробовать еще большую сеть, но сетевой ответ никогда не перегружал бы данные. Это устраняет догадки, необходимые для определения оптимального размера сети.
При использовании trainbr, важно позволить алгоритму запускаться до тех пор, пока эффективное количество параметров не сойдется. Обучение может быть остановлено с сообщением «Maximum MU learned». Это типично и является хорошим показателем того, что алгоритм действительно сходился. Можно также сказать, что алгоритм сходился, если суммарная квадратичная невязка (SSE) и суммарные квадратные веса (SSW) являются относительно постоянными в течение нескольких итераций. В этом случае можно нажать кнопку Остановить обучение в окне обучения.
Ранняя остановка и регуляризация могут обеспечить обобщение сети, когда вы применяете их правильно.
Для ранней остановки вы должны быть осторожны, чтобы не использовать алгоритм, который сходится слишком быстро. Если вы используете быстрый алгоритм (например, trainlm), установите параметры обучения так, чтобы сходимость была относительно медленной. Для примера задайте mu к относительно большому значению, такому как 1, и задать mu_dec и mu_inc к значениям, близким к 1, таким как 0,8 и 1,5, соответственно. Функции обучения trainscg и trainbr обычно хорошо работают с ранней остановкой.
С ранней остановкой выбор набора валидации также важен. Набор валидации должен быть показательным для всех точек в набор обучающих данных.
Когда вы используете байесовскую регуляризацию, важно обучать сеть, пока она не достигнет сходимости. Суммарная квадратная ошибка, суммарные квадратные веса и эффективное количество параметров должны достигать постоянных значений, когда сеть сходится.
С ранней остановкой и регуляризацией рекомендуется обучать сеть, начиная с нескольких различных начальных условий. Возможен отказ любого из методов при определенных обстоятельствах. При тестировании нескольких различных начальных условий можно проверить устойчивую эффективность сети.
Когда набор данных является маленьким, и вы обучаете приближение функций сетей, байесовская регуляризация обеспечивает лучшая эффективность обобщения, чем ранняя остановка. Это связано с тем, что байесовская регуляризация не требует, чтобы набор данных валидации был отделен от набора обучающих данных; он использует все данные.
Чтобы дать некоторое представление о эффективности алгоритмов, как ранняя остановка, так и байесовская регуляризация были протестированы на нескольких наборах данных бенчмарка, которые перечислены в следующей таблице.
Заголовок набора данных | Число точек | Сеть | Описание |
|---|---|---|---|
МЯЧ | 67 | 2-10-1 | Калибровка с двумя датчиками для измерения положения мяча |
СИНУС (5% N) | 41 | 1-15-1 | Одноциклическая синусоида с Гауссовым шумом на уровне 5% |
СИНУС (2% N) | 41 | 1-15-1 | Одноциклическая синусоида с Гауссовым шумом на уровне 2% |
ENGINE (ВСЕ) | 1199 | 2-30-2 | Датчик Engine - полный набор данных |
ENGINE (1/4) | 300 | 2-30-2 | Датчик Engine - 1/4 набора данных |
ХОЛЕСТ (ВСЕ) | 264 | 5-15-3 | Измерение холестерина - полный набор данных |
ХОЛЕСТ (1/2) | 132 | 5-15-3 | Измерение холестерина - набор данных 1/2 |
Эти наборы данных имеют различные размеры с различным количеством входов и целей. С двумя наборами данных сети были обучены один раз с использованием всех данных и затем переобучены с использованием только части данных. Это иллюстрирует, как преимущество байесовской регуляризации становится более заметным, когда наборы данных меньше. Все наборы данных получаются из физических систем, за исключением наборов данных SINE. Эти два были искусственно созданы путем добавления различных уровней шума к одному циклу синусоиды. Эффективность алгоритмов на этих двух наборах данных иллюстрирует эффект шума.
В следующей таблице обобщены эффективность ранней остановки (ES) и байесовской регуляризации (BR) на семи тестовых наборах. (The trainscg алгоритм использовался для ранних остановочных тестов. Другие алгоритмы обеспечивают аналогичную эффективность.)
Средняя квадратичная ошибка набора тестов
| Метод | Мяч | Engine (все) | Engine (1/4) | Холз (Все) | Холл (1/2) | Синус (5% N) | Синус (2% N) |
|---|---|---|---|---|---|---|---|
| ES | 1.2e-1 | 1.3e-2 | 1.9e-2 | 1.2e-1 | 1.4e-1 | 1.7e-1 | 1.3e-1 |
| BR | 1.3e-3 | 2.6e-3 | 4.7e-3 | 1.2e-1 | 9.3e-2 | 3.0e-2 | 6.3e-3 |
| ES/BR | 92 | 5 | 4 | 1 | 1.5 | 5.7 | 21 |
Вы можете увидеть, что байесовская регуляризация работает лучше, чем ранняя остановка в большинстве случаев. Улучшение эффективности наиболее заметно, когда набор данных небольшой, или если в наборе данных мало шума. Набор данных МЯЧ, например, был получен с датчиков, которые имели очень мало шума.
Несмотря на то, что обобщающая эффективность байесовской регуляризации часто лучше, чем ранняя остановка, это не всегда так. В сложение, форма байесовской регуляризации, реализованная в тулбоксе, не так хорошо работает с задачами распознавания шаблона, как с приближением функций задачами. Это потому, что приближение к Гессиану, которое используется в алгоритме Левенберга-Марквардта, не так точно, когда выход сети насыщен, как в случае с задачами распознавания шаблонов. Другой недостаток байесовского метода регуляризации заключается в том, что сходимость обычно занимает больше времени, чем ранняя остановка.
Эффективность обученной сети может в некоторой степени измеряться ошибками на наборах обучения, валидации и тестах, но часто полезно исследовать сетевую реакцию более подробно. Одним из опций является выполнение регрессионного анализа между сетевым ответом и соответствующими целями. Рутинная regression предназначен для выполнения этого анализа.
Следующие команды иллюстрируют, как выполнить регрессионный анализ в обученной сети.
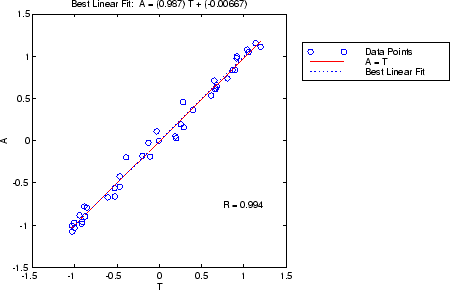
x = [-1:.05:1]; t = sin(2*pi*x)+0.1*randn(size(x)); net = feedforwardnet(10); net = train(net,x,t); y = net(x); [r,m,b] = regression(t,y)
r =
0.9935
m =
0.9874
b =
-0.0067
Выходы сети и соответствующие цели передаются в regression. Это возвращает три параметра. Первые два, m и b, соответствуют наклону и свободный член наилучшей линейной регрессии, относящейся к выходам сети. Если бы была идеальная подгонка (выходы точно равны целям), наклон был бы равен 1, а свободный член был бы равен 0. В этом примере можно увидеть, что цифры очень близки. Третья переменная, возвращенная regression - коэффициент корреляции (R-значение) между выходами и целевыми объектами. Это мера того, насколько хорошо изменение выхода объясняется целями. Если это число равно 1, тогда существует идеальная корреляция между целями и выходами. В примере число очень близко к 1, что указывает на хорошую подгонку.
Следующий рисунок иллюстрирует графический выход, предоставляемый regression. Выходы сети строятся по сравнению с целями как открытые круги. Лучшая линейная подгонка обозначена штриховой линией. Идеальная подгонка (выход, равный целям) обозначается сплошной линией. В этом примере трудно отличить лучшую линейную линию подгонки от идеальной линии подгонки, потому что подгонка так хороша.