Документация

Проектирование временных рядов нейронных сетей с задержкой по времени

Начните с самой простой динамической сети, которая состоит из сети прямого распространения с выделенной линией задержки на входе. Это называется сфокусированной нейронной сетью с задержкой по времени (FTDNN). Это часть общего класса динамических сетей, называемых сфокусированными сетями, в которых динамика появляется только на входном слое статической многослойной сети прямого распространения. Следующий рисунок иллюстрирует двухуровневый FTDNN.

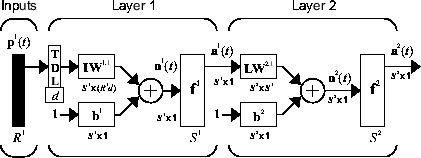
Эта сеть хорошо подходит для предсказания timeseries. Следующий пример - использование FTDNN для предсказания классических временных рядов.

Следующий рисунок является графиком нормализованных данных о интенсивности, записанных с дальнего инфракрасного лазера в хаотическом состоянии. Это часть одного из нескольких наборов данных, используемых для конкурса временных рядов Santa Fe [WeGe94]. В конкурсе цель состояла в том, чтобы использовать первые 1000 точек временных рядов, чтобы предсказать следующие 100 очков. Поскольку наша цель состоит в том, чтобы просто проиллюстрировать, как использовать FTDNN для предсказания, сеть обучена здесь, чтобы выполнить одноэтапные прогнозы. (Можно использовать получившуюся сеть для многоступенчатых предсказаний, отправляя предсказания назад на вход сети и продолжая итерацию.)

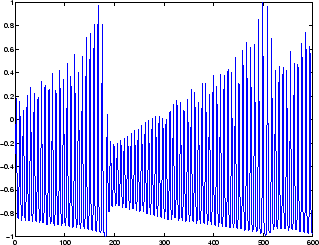
Первым шагом является загрузка данных, их нормализация и преобразование во временную последовательность (представленную массивом ячеек):

y = laser_dataset;
y = y(1:600);

Теперь создайте сеть FTDNN, используя timedelaynet команда. Эта команда аналогична команде feedforwardnet Команда с дополнительным входом вектора линии задержки (первый вход). В данном примере используйте выделенную линию задержки с задержками от 1 до 8 и используйте десять нейронов в скрытом слое:

ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';

Организуйте входы сети и целевые параметры для обучения. Поскольку сеть имеет выделенную линию задержки с максимальной задержкой 8, начните с предсказания девятого значения временных рядов. Вы также должны загрузить выделенную линию задержки с восемью начальными значениями временных рядов (содержащимися в переменной Pi):

p = y(9:end);
t = y(9:end);
Pi=y(1:8);
ftdnn_net = train(ftdnn_net,p,t,Pi);

Заметьте, что вход в сеть аналогичен целевому. Поскольку сеть имеет минимальную задержку в один временной шаг, это означает, что вы выполняете одноэтапное предсказание.

Во время обучения появляется следующее окно обучения.

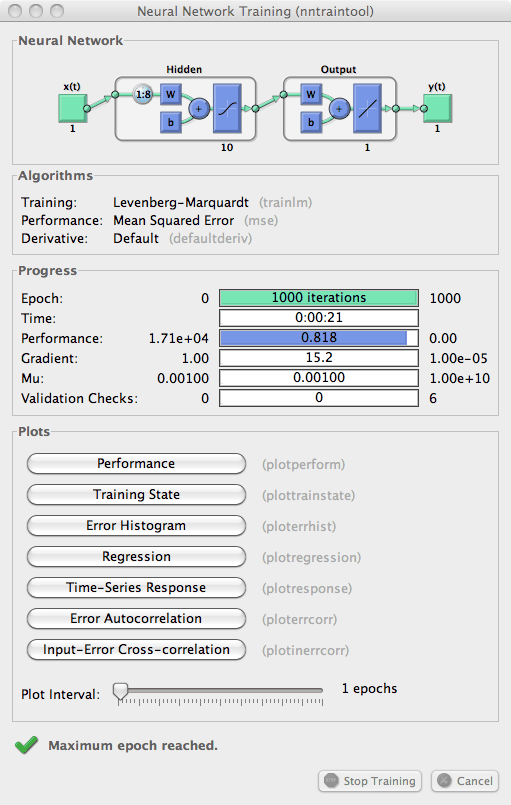
Обучение остановилось, потому что была достигнута максимальная эпоха. В этом окне можно отобразить ответ сети, нажав на Time-Series Response. Появится следующий рисунок.

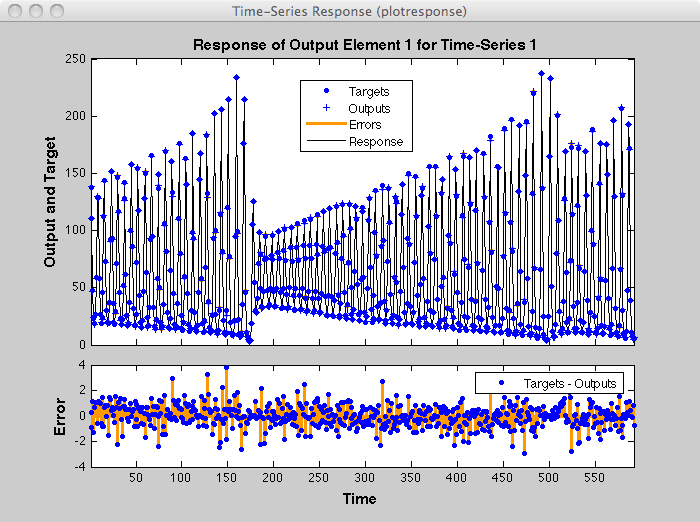
Теперь симулируйте сеть и определите ошибку предсказания.

yp = ftdnn_net(p,Pi);
e = gsubtract(yp,t);
rmse = sqrt(mse(e))

rmse =
    0.9740

(Обратите внимание, что gsubtract является общей функцией вычитания, которая может работать с массивами ячеек.) Этот результат намного лучше, чем вы могли бы получить с помощью линейного предиктора. Можно проверить это с помощью следующих команд, которые проектируют линейный фильтр с тем же входом линии задержки, что и предыдущий FTDNN.

lin_net = linearlayer([1:8]);
lin_net.trainFcn='trainlm';
[lin_net,tr] = train(lin_net,p,t,Pi);
lin_yp = lin_net(p,Pi);
lin_e = gsubtract(lin_yp,t);
lin_rmse = sqrt(mse(lin_e))

lin_rmse =
	21.1386

The rms ошибка 21.1386 для линейного предиктора, но 0.9740 для нелинейного предиктора FTDNN.

Одной из приятных функций FTDNN является то, что для вычисления сетевого градиента не требуется динамическая обратная реализация. Это связано с тем, что выделенная линия задержки появляется только на входе сети и не содержит циклов обратной связи или регулируемых параметров. По этой причине вы обнаружите, что эта сеть обучается быстрее, чем другие динамические сети.

Если у вас есть приложение для динамической сети, сначала попробуйте линейную сеть (linearlayer) и далее FTDNN (timedelaynet). Если ни одна из сетей не является удовлетворительной, попробуйте одну из более сложных динамических сетей, обсуждаемых в оставшейся части этой темы.

Каждый раз, когда нейронная сеть обучается, может привести к другому решению из-за различных начальных значений веса и смещения и различных делений данных в наборы для обучения, валидации и тестирования. В результате различные нейронные сети, обученные одной и той же задаче, могут выдавать различные выходы для одного и того же входа. Чтобы убедиться, что нейронная сеть с хорошей точностью была найдена, переобучите несколько раз.

Существует несколько других методов улучшения начальных решений, если желательна более высокая точность. Для получения дополнительной информации см. «Улучшение обобщения неглубоких нейронных сетей» и «Избегайте избыточного оснащения».

p = y(9:end);
t = y(9:end);
Pi = y(1:8);

[p,Pi,Ai,t] = preparets(ftdnn_net,y,y);

[X,Xi,Ai,T,EW,shift] = preparets(net,inputs,targets,feedback,EW)