Определите коэффициенты линейных предикторов N-го порядка
Оценка/линейное предсказание
dsplp
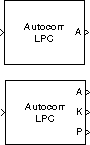
Блок Автокорреляция LPC определяет коэффициенты N-шага прямого линейного предиктора для timeseries в каждом M по длине входном канале, u, путем минимизации ошибки предсказания в смысле наименьших квадратов. Линейный предиктор является конечная импульсная характеристика, который предсказывает следующее значение в последовательности из настоящего и прошлого входов. Этот метод имеет приложения в создании фильтра, кодировании речи, спектральном анализе и системе идентификации.
Блок Автокорреляция LPC может вывести ошибку предсказания для каждого канала как полиномиальные коэффициенты, коэффициенты отражения или оба. Это также может вывести степень ошибки предсказания для каждого канала. Вход u может быть неориентированным вектором, вектором-столбцом или матрицей. Векторы-строки не являются допустимыми входами. Блок обрабатывает все входные M -by N матрицы как N канала M длины.
Когда вы выбираете Inherit prediction order from input dimensions, порядок предсказания, N, наследуется от входа размерностей. В противном случае можно использовать параметр Prediction order, чтобы задать значение N. Обратите внимание, что N должен быть скаляром со значением, меньше длины входных каналов, или блок вызывает ошибку.
Когда Output(s) установлено на A, порт А включен. Для каждого канала порт A выводит (N + 1) вектор-на-1 столбец, a = [1
a2 a3... aN+1]T, содержащий коэффициенты линейного процесса скользящего среднего значения (MA) N-го порядка, который предсказывает следующее значение, ûM+1, во входном timeseries.
Когда Output(s) установлено на K, порт K включен. Для каждого канала порт K выводит вектор- N столбец, элементами которого являются коэффициенты отражения ошибки предсказания. Когда Output(s) установлено на A and Kоба порта А и K активизированы, и каждый порт выводит свой соответствующий набор коэффициентов предсказания для каждого канала.
Когда вы выбираете Output prediction error power (P), порт P включен. Степень ошибки предсказания выводится в порт P как вектор, длина которого является количеством входа каналов.
Блок Автокорреляция LPC вычисляет решение методом наименьших квадратов
где указывает на 2-норму и
Решение задачи наименьших квадратов через нормальные уравнения
приводит к системе уравнений
где r = [r1 r2 r3... rn+1] T является оценкой автокорреляции для u, вычисленных с использованием блока Autocorrelation, и * указывает на комплексную сопряженную транспозицию. Нормальные уравнения решены в O (n2) операции блоком Левинсона-Дурбина.
Обратите внимание, что решение задачи LPC очень тесно связано с методом AR Юла-Уокера спектральной оценки. В этом контексте нормальные уравнения выше называются уравнениями AR Юла-Уокера.
Тип коэффициентов предсказания, выводимых блоком. Блок может выводить полиномиальные коэффициенты (A), коэффициенты отражения (K), или и то и другое (A and K).
Когда выбран, включает P портов, который выводит выходную степень ошибки предсказания.
При выборе блок наследует порядок предсказания от входа измерений.
Задайте порядок предсказания, N, который должен быть скаляром. Этот параметр отключен, когда вы выбираете параметр Inherit prediction order from input dimensions.
Haykin, S. Adaptive Filter Theory. 3-й эд. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1996.
Ljung, L. Система идентификации: Теория для пользователя. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1987. PGS. 278-280.
Проакис, Дж. и Д. Манолакис. Цифровая обработка сигналов. 3-й эд. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1996.
Плавающая точка двойной точности
Плавающая точка с одной точностью
| Autocorrelation | DSP System Toolbox |
| Levinson-Durbin | DSP System Toolbox |
| Yule-Walker Method | DSP System Toolbox |
lpc | Signal Processing Toolbox |