Levinson-Durbin

Решите линейную систему уравнений, используя рекурсию Левинсона-Дурбина

Библиотека

Математические функции/матрицы и линейная алгебра/линейные системные решатели

dspsolvers

Описание

Блок Левинсона-Дурбина решает систему линейных уравнений n-го порядка

Ra = b

в случаях, когда:

R - эрмитова, положительно-определенная, матрица Теплица.
b идентично первому столбцу R со сдвигом на один элемент и с противоположным знаком.

$[\begin{matrix} r (1) & r^{*} (2) & \dots & r^{*} (n) \\ r (2) & r (1) & \dots & r^{*} (n - 1) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ r (n) & r (n - 1) & \dots & r (1) \end{matrix}] [\begin{matrix} a (2) \\ a (3) \\ ⋮ \\ a (n + 1) \end{matrix}] = [\begin{matrix} - r (2) \\ - r (3) \\ ⋮ \\ - r (n + 1) \end{matrix}]$

Вход в блок, r = [r(1) r(2) ... r(n+1)], может быть вектором или матрицей. Если вход является матрицей, блок обрабатывает каждый столбец как независимый канал и решает его отдельно. Каждый канал входа содержит лаги, 0 через n автокорреляционной последовательности, которые появляются в матричном R.

Блок может выводить полиномиальные коэффициенты, A, коэффициенты отражения, K и степень ошибки предсказания, P, в различных комбинациях. Параметр Output(s) позволяет включать A и K выходов путем выбора одной из следующих настроек:

A - Для каждого канала порт А выводит A = [1 a(2) a(3) ... a(n+1)], решение уравнения Левинсона-Дурбина. A имеет ту же размерность, что и вход. Можно также просмотреть элементы каждого выходного канала как коэффициенты процесса авторегрессии n-го порядка (AR).
K - Для каждого канала порт K выводит K = [k(1) k(2) ... k(n)], который содержит n коэффициентов отражения и имеет ту же размерность, что и вход, меньше одного элемента. Скалярный входной канал вызывает ошибку, когда вы выбираете K. Можно использовать коэффициенты отражения, чтобы реализовать представление решетки процесса AR, описанного ниже на этой странице.
A and K - Блок выводит оба представления в соответствующих портах. Скалярный входной канал вызывает ошибку, когда вы выбираете A and K.

Установите флажок Output prediction error power (P), чтобы вывести степень ошибки предсказания для каждого канала, P. Для каждого канала P представляет степень выхода конечной импульсной характеристики с отводами A и входной автокорреляцией, описанной r, где A представляет фильтр ошибки предсказания, и r является входом в блок. В этом случае A является отбеливающим фильтром. P имеет по одному элементу на входной канал.

Когда вы устанавливаете флажок If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0 (по умолчанию), канал входа, r которого (1) элемент с нулем генерирует нулевой выход. Когда вы снимаете этот флажок, вход с r (1) = 0 производит NaNs в выходах. В целом вход с r (1) = 0 недопустим, поскольку он не создает положительно-определенную матричную R. Часто, однако, блоки получают нулевые входы в начале симуляции. Флажок позволяет избегать распространения NaNs в течение этого периода.

Приложения

Одно из применений композиции Левинсона-Дурбина, реализованное этим блоком, находится в задаче AR Юла-Уокера, которая касается моделирования неизвестной системы как авторегрессивного процесса. Вы бы смоделировали такой процесс, как выход полнополюсного БИХ с белым Гауссовым шумом. В задаче Юле-Уокера использование автокорреляционной последовательности сигнала для получения оптимальной оценки приводит к уравнению R a = b типа, показанного выше, которое наиболее эффективно решается рекурсией Левинсона-Дурбина. В этом случае вход в блок представляет автокорреляционную последовательность с r(1) являющийся значением нулевой задержки. Затем выход порта A блока содержит коэффициенты авторегрессивного процесса, которые оптимально моделируют систему. Коэффициенты упорядочены в нисходящих степенях z, и процесс AR является минимальной фазой. Ошибка предсказания, G, задает коэффициент усиления для неизвестной системы, где $G = \sqrt{P}$ :

$H (z) = \frac{G}{A (z)} = \frac{G}{1 + a (2) z^{- 1} + ... + a (n + 1) z^{- n}}$

Выход в порту K блока содержит соответствующие коэффициенты отражения, [<reservedrangesplaceholder1> <reservedrangesplaceholder0> <reservedrangesplaceholder1> <reservedrangesplaceholder0> <reservedrangesplaceholder1> <reservedrangesplaceholder0>, для решетки реализации этого БИХ. Блок Yule-Walker AR Estimator реализует этот основанный на автокорреляции метод для оценки AR- модели, в то время как блок Метода Юла-Уокера расширяет способ до спектральной оценки.

Другое распространенное применение алгоритма Левинсона-Дурбина - в линейном прогнозирующем кодировании, которое касается нахождения коэффициентов процесса скользящего среднего значения (MA) (или конечная импульсная характеристика), который предсказывает следующее значение сигнала из текущей выборки сигнала и конечное число прошлых выборок. В этом случае вход в блок представляет автокорреляционную последовательность сигнала с r (1) будучи значением нулевой задержки, и выход порта A блока содержит коэффициенты прогнозирующего процесса MA (в нисходящих степенях z).

$H (z) = A (z) = 1 + a (2) z^{- 1} + ... a (n + 1) z^{- n}$

Эти коэффициенты решают следующую задачу оптимизации:

$\overset{\min}{{a_{i}}}$

$E [{| x_{n} - \sum_{i = 1}^{N} a_{i} x_{n - i} |}^{2}]$

Снова, выход в порту K блока содержит соответствующие коэффициенты отражения, [k(1) k(2) ... k(n)], для решетки реализации этой конечной импульсной характеристики. Блок Autocorrelation LPC в библиотеке Linear Prediction реализует этот метод предсказания на основе автокорреляции.

Типы данных с фиксированной точкой

Схемы в этом разделе показывают типы данных, используемые в блоке Левинсона-Дурбина для сигналов с фиксированной точкой.

После инициализации блок выполняет n обновления. При обновлении (j + 1),

$value in accumulator = r (j + 1) + \sum a_{j} (i) \times r (j - i + 1)$

Следующая схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

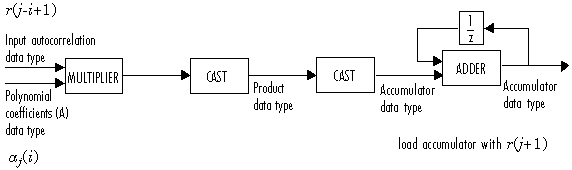
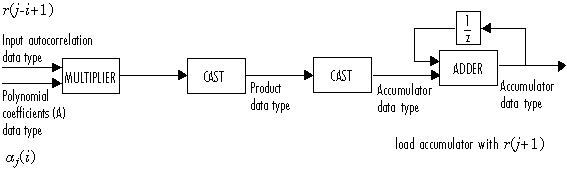
Затем блок обновляет коэффициенты отражения K согласно

$K_{j + 1} = значение в аккумуляторе / P_{j}$

Блок затем обновляет степень ошибки предсказания P согласно

$P_{j + 1} = P_{j} - P_{j} \times K_{j + 1} \times союз (K_{j + 1})$

Следующая схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

Полиномиальные коэффициенты A затем обновляются согласно

$a_{j + 1} (i) = a_{j} (i) + K_{j + 1} \times союз (a_{j} (j - 1 + i))$

Эта схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

Алгоритм

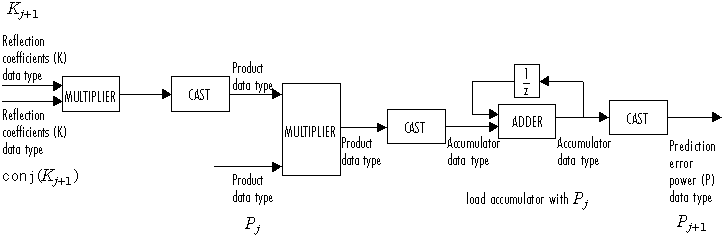
Алгоритм требует O (n²) операции для каждого входного канала. Поэтому эта реализация намного более эффективна для больших n, чем стандартное Гауссовское устранение, которое требует O (n³) операции по каналу.

Параметры

Main Tab

Output(s)

Задайте представление решения R a = b для вывода: коэффициенты модели (A), коэффициенты отражения (K), или и то и другое (A and K). Когда вход является скаляром или вектором-строкой, вы должны задать этот параметр A.

Output prediction error power (P)

Выберите для вывода ошибки предсказания на порт P.

If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0

Когда вы устанавливаете этот флажок и первый элемент входа, r(1), равен нулю, блок выводит, при необходимости, следующие векторы:

A = [1 zeros(1,n)]
K = [zeros(1,n)]
P = 0

Когда вы снимаете этот флажок, блок выводит вектор NaNs для каждого канала, чья r(1) элемент равен нулю.

Data Types Tab

Примечание

Наследование с плавающей точкой имеет приоритет над параметрами типа данных, заданными на этой панели. Когда входы являются плавающими точками, блок игнорирует эти настройки, и все внутренние типы данных являются плавающими точками.

Rounding mode

Задайте режим округления для операций с фиксированной точкой как один из следующих:

Floor
Ceiling
Convergent
Nearest
Round
Simplest
Zero

Для получения дополнительной информации смотрите режим округления.

Saturate on integer overflow

Когда вы выбираете этот параметр, блок насыщает результат своей операции с фиксированной точкой. Когда вы очищаете этот параметр, блок переносит результат своей операции с фиксированной точкой. Для получения дополнительной информации о saturate и wrap, см. Режим переполнения для операций с фиксированной точкой.

Product output

Укажите тип выходных данных продукта. Смотрите Типы данных с фиксированной точкой и Типы данных умножения для рисунков, описывающих использование типа выходных данных продукта в этом блоке. Вы можете установить его на:

Правило, которое наследует тип данных, например Inherit: Same as input
Выражение, которое вычисляет допустимый тип данных, например fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, которая помогает вам задать параметр Product output.

Дополнительные сведения см. в разделе «Установка типов данных с использованием помощника по типам данных» (Simulink).

Accumulator

Задайте тип данных аккумулятора. См. типы данных с фиксированной точкой для рисунков, описывающих использование типа данных аккумулятора в этом блоке. Вы можете установить его на:

Правило, которое наследует тип данных, например Inherit: Same as input
Правило, которое наследует тип данных, например Inherit: Same as product output
Выражение, которое вычисляет допустимый тип данных, например fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, которая помогает вам задать параметр Accumulator.

Polynomial coefficients (A)

Задайте тип данных полиномиальных коэффициентов (A). См. типы данных с фиксированной точкой для рисунков, описывающих использование типа данных A в этом блоке. Можно задать для него выражение, которое вычисляет допустимый тип данных, например fixdt(1,16,15).

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, которая помогает вам задать параметр A.

Reflection coefficients (K)

Задайте тип данных полиномиальных коэффициентов (A). См. типы данных с фиксированной точкой для рисунков, описывающих использование типа данных K в этом блоке. Можно задать для него выражение, которое вычисляет допустимый тип данных, например fixdt(1,16,15).

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, которая помогает вам задать параметр K.

Prediction error power (P)

Задайте тип данных степени (P) ошибки предсказания. См. типы данных с фиксированной точкой для рисунков, описывающих использование типа данных P в этом блоке. Вы можете установить его на:

Правило, которое наследует тип данных, например Inherit: Same as input
Выражение, которое вычисляет допустимый тип данных, например fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, которая помогает вам задать параметр P.

Minimum

Задайте минимальные значения, которые должны иметь полиномиальные коэффициенты, коэффициенты отражения или степень ошибки предсказания. Значение по умолчанию [] (не определено). Simulink^® использует это значение для выполнения:

Проверка области значений параметров (см. «Задание минимальных и максимальных значений для параметров блоков (Simulink)»)
Автоматическое масштабирование типов данных с фиксированной точкой

Maximum

Задайте максимальные значения, которые должны иметь полиномиальные коэффициенты, коэффициенты отражения или степень ошибки предсказания. Значение по умолчанию [] (не определено). Simulink использует это значение для выполнения:

Проверка области значений параметров (см. «Задание минимальных и максимальных значений для параметров блоков (Simulink)»)
Автоматическое масштабирование типов данных с фиксированной точкой

Lock data type settings against changes by the fixed-point tools

Выберите этот параметр, чтобы инструменты с фиксированной точкой не переопределяли типы данных, заданные в маске блока.

Ссылки

Голубь, Г. Х. и К. Ф. Ван Лоун. Секта. 4.7 в матричных расчетах. 3-й эд. Балтимор, доктор медицинских наук: Johns Hopkins University Press, 1996.

Ljung, L. Система идентификации: Теория для пользователя. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1987. PGS. 278–280.

Кей, Стивен М. Современная спектральная оценка: теория и применение. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1988.

Поддерживаемые типы данных

Плавающая точка двойной точности
Плавающая точка с одной точностью
Фиксированная точка (только со знаком)
8-, 16- и 32-битные целые числа со знаком

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Сгенерированный код опирается на memcpy или memset функции (string.h) при определенные обстоятельства.

Преобразование с фиксированной точкой
Разрабатывайте и моделируйте системы с фиксированной точкой с помощью Fixed-Point Designer™.

Если вход является фиксированной точкой, он должен быть подписанным целым числом или подписанной фиксированной точкой с степенью двойки и нулевым смещением.

См. также

Функции

levinson

Блоки

Autocorrelation LPC | Cholesky Solver | LDL Solver | LU Solver | QR Solver | Yule-Walker AR Estimator | Yule-Walker Method

Документация

Levinson-Durbin

Библиотека