dsp.HampelFilter

Фильтруйте выбросы с помощью идентификатора Хампеля

Описание

The dsp.HampelFilter Система object™ обнаруживает и удаляет выбросы входного сигнала с помощью идентификатора Хампеля. Этот Идентификатор Хампеля является изменением правила статистики с тремя сигмами, которое устойчиво к выбросам. Для каждой выборки входного сигнала объект вычисляет медиану окна, состоящего из текущей выборки и $\frac{L e n - 1}{2}$ смежные выборки с каждой стороны токовой выборки. Len - длина окна, заданная вами через WindowLength свойство. Объект также оценивает стандартное отклонение каждой выборки относительно ее медианы окна с помощью медианного абсолютного отклонения. Если выборка отличается от медианы больше, чем порог, умноженный на стандартное отклонение, фильтр заменяет выборку на медиану. Для получения дополнительной информации см. «Алгоритмы».

Для фильтрации входного сигнала с помощью идентификатора Хампеля:

Создайте dsp.HampelFilter Объекту и установите его свойства.
Вызывайте объект с аргументами, как будто это функция.

Дополнительные сведения о работе системных объектов см. в разделе «Что такое системные объекты?».

Создание

Синтаксис

hampFilt = dsp.HampelFilter

hampFilt = dsp.HampelFilter(Len)

hampFilt = dsp.HampelFilter(Len, Lim)

hampFilt = dsp.HampelFilter(Name,Value)

Описание

hampFilt = dsp.HampelFilter возвращает объект фильтра Hampel, hampFilt, с использованием свойств по умолчанию.

пример

hampFilt = dsp.HampelFilter(Len) устанавливает WindowLength свойство к Len.

hampFilt = dsp.HampelFilter(Len, Lim) устанавливает WindowLength свойство к Len и Threshold свойство к Lim.

Пример: hampFilt = dsp.HampelFilter(11,2);

hampFilt = dsp.HampelFilter(Name,Value) задает свойства используя Name,Value пар. Неопределенные свойства имеют значения по умолчанию.

Свойства

расширить все

Если не указано иное, свойства являются нетронутыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируются, когда вы вызываете их, и release функция разблокирует их.

Если свойство настраивается, можно изменить его значение в любой момент.

Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Использование Системных объектов.

Если свойство указано как настраиваемое, то можно изменить его значение даже при блокировке объекта.

`WindowLength` - Длина раздвижного окна
`11` (по умолчанию) | положительное нечетное скалярное целое число

Длина скользящего окна, заданная как положительное нечетное скалярное целое число. Окно конечной длины скользит по данным, и объект вычисляет медианное и медианное абсолютное отклонение данных в окне.

Типы данных: single | double

`Threshold` - Порог для определения выбросов
3 (по умолчанию) | положительный действительный скаляр

Порог для определения выбросов, заданное как положительный действительный скаляр. Для получения информации о том, как это свойство используется для обнаружения выбросов, см. Алгоритмы.

Настраиваемый: Да

Типы данных: single | double

Использование

Синтаксис

y = hampFilt(x)

[y,isOutlier] = hampFilt(x)

Описание

пример

y = hampFilt(x) обнаруживает и удаляет выбросы каждого канала входного сигнала, x, независимо с течением времени с использованием фильтра Хэмпеля.

[y,isOutlier] = hampFilt(x) возвращает логический массив, isOutlier, в котором каждый true элемент указывает, что соответствующий элемент во входе является выбросами. isOutlier - тот же размер, что и входной и выходной векторы.

Входные параметры

расширить все

`x` - Вход данных
вектор | матрица

Вход данных, заданный как вектор или матрица. Объект принимает многоканальные входы, то есть m входные входы -by n size, где m ≥ 1 и n > 1. m - количество выборок в каждой системе координат (канале), а n - количество каналов. Объект также принимает входы переменного размера. После того, как объект заблокирован, можно изменить размер каждого входного канала, но вы не можете изменить количество каналов.

Типы данных: single | double

Выходные аргументы

расширить все

`y` - Отфильтрованные данные
вектор | матрица

Отфильтрованные данные, возвращенные в виде вектора или матрицы.

Типы данных: single | double

`isOutlier` - Указать выбросы
`true` | `false`

Логический массив, элементы которого указывают, является ли соответствующий элемент массива входа выбросов. Если элемент в isOutlier является trueсоответствующий элемент массива входа является выбросами.

Типы данных: logical

Функции объекта

Чтобы использовать функцию объекта, задайте системный объект в качестве первого входного параметра. Например, чтобы освободить системные ресурсы системного объекта с именем obj, используйте следующий синтаксис:

release(obj)

расширить все

Общий для всех системных объектов

`step`	Запуск алгоритма системного объекта
`release`	Отпустите ресурсы и допустите изменения в значениях свойств системного объекта и входных характеристиках
`reset`	Сброс внутренних состояний Системного объекта

Примеры

свернуть все

Удаление высокочастотного шума с помощью фильтра Hampel

Открыть скрипт

Фильтруйте высокочастотный шум от сигнала шумовой синусоиды с помощью фильтра Хэмпеля. Сравните эффективность фильтра Хэмпеля с медианным фильтром.

Инициализация

Настройка dsp.HampelFilter и a dsp.MedianFilter объект. Эти объекты используют метод раздвижного окна с длиной окна 7. Создайте временные возможности для просмотра выхода.

Fs = 1000;
hampFilt = dsp.HampelFilter(7);
medFilt = dsp.MedianFilter(7);
scope  = timescope('SampleRate',Fs, ...
    'TimeSpanOverrunAction','Scroll', ...
    'TimeSpanSource','Property',...
    'TimeSpan',1,'ShowGrid',true, ...
    'LayoutDimensions',[3 1], ...
    'NumInputPorts',3);
scope.ActiveDisplay = 1;
scope.Title = 'Signal + Noise';
scope.YLimits = [-1 3];
scope.ActiveDisplay = 2;
scope.Title = 'Hampel Filter Output (Window Length = 7)';
scope.YLimits = [-1 1];
scope.ActiveDisplay = 3;
scope.Title = 'Median Filter Output (Window Length = 7)';
scope.YLimits = [-1 1];

Фильтрация шумного Sine wave с помощью окна длины 7

Сгенерируйте сигнал шумной синусоиды с частотой 10 Гц. Примените фильтр Хэмпела и медианный объект фильтра к сигналу. Просмотр выхода по временным возможностям.

FrameLength = 256;
sine = dsp.SineWave('SampleRate',Fs,'Frequency',10,...
    'SamplesPerFrame',FrameLength);

for i = 1:500
    hfn = 3 * (rand(FrameLength,1) < 0.02);
    x = sine() + 1e-2 * randn(FrameLength,1) + hfn;
    y1 = hampFilt(x);
    y2 = medFilt(x);
    scope(x,y1,y2);
end
release(scope)

Оба фильтра удаляют высокочастотный шум. Однако при увеличении длины окна предпочтительным является фильтр Хэмпеля. В отличие от медианного фильтра, фильтр Хэмпеля сохраняет форму синусоиды даже с большими длинами окон.

Фильтрация шумного Sine wave с помощью окна длины 37

Увеличьте длину окна обоих фильтров до 37. Фильтрация шумной синусоиды и просмотр отфильтрованного выхода на временных возможностях. Чтобы изменить длину окна фильтров, необходимо отпустить объекты фильтра в начале цикла обработки.

release(hampFilt);
release(medFilt);
hampFilt.WindowLength = 37;
medFilt.WindowLength = 37;
scope.ActiveDisplay = 1;
scope.Title = 'Signal + Noise';
scope.ActiveDisplay = 2;
scope.Title = 'Hampel Filter Output (Window Length = 37)';
scope.ActiveDisplay = 3;
scope.Title = 'Median Filter Output (Window Length = 37)';
for i = 1:500
    hfn = 3 * (rand(FrameLength,1) < 0.02);
    x = sine() + 1e-2 * randn(FrameLength,1) + hfn;
    y1 = hampFilt(x);
    y2 = medFilt(x);
    scope(x,y1,y2);
end
release(scope)

Медианный фильтр уплощает гребни и впадины синусоиды из-за медианной операции над большим окном данных. Фильтр Хэмпела сохраняет форму сигнала, в дополнение к удалению выбросов.

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпеля

Открыть скрипт

Удалите высокочастотные выбросы из потокового сигнала с помощью dsp.HampelFilter Системные object™.

Используйте dsp.MatFileReader Системный объект для чтения файла MAT гироскопа. Файл содержит три столбца данных, причем каждый столбец содержит 7140 выборки. Три столбца представляют данные о оси X, оси Y и оси Z от датчика движения гироскопа. Выберите формат кадра 714 выборок, чтобы каждый столбец данных содержал 10 системы координат. The dsp.HampelFilter Системный объект использует длину окна 11. Создайте timescope объект для просмотра отфильтрованных выходов.

reader = dsp.MatFileReader('SamplesPerFrame',714,'Filename','LSM9DSHampelgyroData73.mat', ...
    'VariableName','data');
hampFilt = dsp.HampelFilter(11);
scope = timescope('NumInputPorts',1,'SampleRate',119,'YLimits',[-300 300], ...
    'ChannelNames',{'Input','Filtered Output'},...
    'TimeSpanSource','Property','TimeSpan',60,'ShowLegend',true);

Фильтрация данных гироскопа с помощью dsp.HampelFilter Системный объект. Просмотрите отфильтрованные данные по оси Z в Time Scope.

for i = 1:10
    gyroData = reader();
    filteredData = hampFilt(gyroData);
    scope([gyroData(:,3),filteredData(:,3)]);
end

Фильтр Хэмпела удаляет все выбросы и сохраняет форму сигнала.

Подробнее о

расширить все

Идентификатор Хампеля

Этот Идентификатор Хампеля является изменением правила статистики с тремя сигмами, которое устойчиво к выбросам.

Учитывая последовательность x 1, _x 2, x 3, .._., xn и скользящее окно k длины, задайте медиану «точка-точка» и оценки стандартного отклонения с помощью:

Локальная медиана - $m_{i} = median (x_{i - k}, x_{i - k + 1}, x_{i - k + 2}, \dots, x_{i}, \dots, x_{i + k - 2}, x_{i + k - 1}, x_{i + k})$
Стандартное отклонение - $σ_{i} = κ median (| x_{i - k} - m_{i} |, \dots, | x_{i + k} - m_{i} |),$ где $κ = \frac{1}{\sqrt{2} {erfc}^{- 1} (1 / 2)} \approx 1.4826$

Величина _σi / κ известна как медианное абсолютное отклонение (MAD).

Если выборочный _xi такой, что

$| x_{i} - m_{i} | > n_{σ} σ_{i}$

для заданного порога _nσ, затем Идентификатор Хампеля объявляет _xi выбросов и заменяет его на _mi. Если _nσ равно 0, то фильтр Хэмпела ведет себя как обычный медианный фильтр.

Алгоритмы

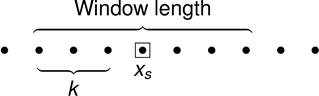
Для заданной выборки данных, _xs, алгоритм:

Центрирует окно нечетной длины в текущей выборке.
Вычисляет локальную медиану, _mi и стандартное отклонение, _σi, над активным окном данных.
Сравнивает текущую выборку с _nσ × _σi, где _nσ - пороговое значение. Если $| x_{s} - m_{i} | > n_{σ} \times σ_{i}$ фильтр идентифицирует текущую выборку, _xs, как выбросы и заменяют ее медианным значением, _mi.

Рассмотрим систему координат данных, которая передается в фильтр Хэмпеля.

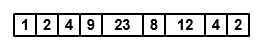
В этом примере фильтр Hampel скользит по данным окном длины 5 (Len). Фильтр имеет порог значение 2 (_nσ). Чтобы иметь полное окно в начале системы координат, алгоритм фильтра готовит систему координат с Len - 1 нулями. Чтобы вычислить первую выборку выхода, окно центрируется на ${[\frac{L e n - 1}{2} + 1]}^{th}$ выборка в добавленной системе координат, третий нуль в этом случае. Фильтр вычисляет медиану, среднее абсолютное отклонение и стандартное отклонение по данным в локальном окне.

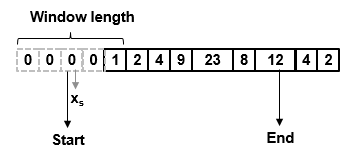
Текущая выборка: _xs = 0.
Окно данных: win = [0 0 0 0 1].
Локальная медиана: _mi = медиана ([0 0 0 0 1]) = 0.
Срединное абсолютное отклонение: $m a d_{i} = median (| x_{i - k} - m_{i} |, \dots, | x_{i + k} - m_{i} |)$ . Для этого окна данных, $m a d = median (| 0 - 0 |, \dots, | 1 - 0 |) = 0$ .
Стандартное отклонение: _σi = κ × _madi = 0, где $κ = \frac{1}{\sqrt{2} {erfc}^{- 1} (1 / 2)} \approx 1.4826$ .
Текущая выборка _xs = 0 не подчиняется отношению для определения выбросов.

$[| x_{s} - m_{i} | = 0] > [(n_{σ} \times σ_{i}) = 0]$
Поэтому фильтр Хэмпела выводит текущую входную выборку, _xs = 0.

Повторите эту процедуру для каждой последующей выборки, пока алгоритм не центрирует окно на ${[E n d - \frac{L e n - 1}{2}]}^{th}$ выборка, отмеченный как End. Потому что окно с центром на последнем $\frac{L e n - 1}{2}$ выборки не могут быть полными, эти выборки обрабатываются следующей системой координат входных данных.

Вот первый выходной кадр, который генерирует фильтр Хэмпеля:

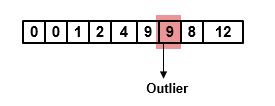
Седьмая выборка добавленного входного кадра 23 является выбросами. Фильтр Хэмпела заменяет эту выборку медианой над локальным окном [4 9 23 8 12].

Ссылки

[1] Боденем, Дин. «Адаптивная фильтрация и обнаружение изменений для потоковых данных». PH.D. Дипломная работа. Имперский колледж, Лондон, 2012.

[2] Лю, Ханьсун, Сириш Шах и Вэй Цзян. «Оперативное определение выбросов и очистка данных». Компьютеры и химическая техника. Том 28, 2004 марта, с. 1635-1647.

[3] Суомела, Юкка. Медианная фильтрация эквивалентна сортировке, 2014.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

Указания и ограничения по применению:

Смотрите Системные объекты в Генерации кода MATLAB (MATLAB Coder).

Документация

dsp.HampelFilter

Описание

Создание

Синтаксис

Описание

Свойства

`WindowLength` - Длина раздвижного окна
`11` (по умолчанию) | положительное нечетное скалярное целое число

`Threshold` - Порог для определения выбросов
3 (по умолчанию) | положительный действительный скаляр

Использование

Синтаксис

Описание

Входные параметры

`x` - Вход данных
вектор | матрица

Выходные аргументы

`y` - Отфильтрованные данные
вектор | матрица

`isOutlier` - Указать выбросы
`true` | `false`

Функции объекта

Общий для всех системных объектов

Примеры

Удаление высокочастотного шума с помощью фильтра Hampel

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпеля

Подробнее о

Идентификатор Хампеля

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

Функции

Объекты

Блоки

Документация DSP System Toolbox

Поддержка

Документация

dsp.HampelFilter

Описание

Создание

Синтаксис

Описание

Свойства

WindowLength - Длина раздвижного окна 11 (по умолчанию) | положительное нечетное скалярное целое число

Threshold - Порог для определения выбросов 3 (по умолчанию) | положительный действительный скаляр

Использование

Синтаксис

Описание

Входные параметры

x - Вход данных вектор | матрица

Выходные аргументы

y - Отфильтрованные данные вектор | матрица

isOutlier - Указать выбросы true | false

Функции объекта

Общий для всех системных объектов

Примеры

Удаление высокочастотного шума с помощью фильтра Hampel

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпеля

Подробнее о

Идентификатор Хампеля

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

Функции

Объекты

Блоки

Документация DSP System Toolbox

Поддержка

`WindowLength` - Длина раздвижного окна
`11` (по умолчанию) | положительное нечетное скалярное целое число

`Threshold` - Порог для определения выбросов
3 (по умолчанию) | положительный действительный скаляр

`x` - Вход данных
вектор | матрица

`y` - Отфильтрованные данные
вектор | матрица

`isOutlier` - Указать выбросы
`true` | `false`

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®