Hampel Filter

Фильтруйте выбросы с помощью идентификатора Хампеля

Библиотека:
DSP System Toolbox/Фильтрация/Проекты фильтров

Описание

Блок Hampel Filter обнаруживает и удаляет выбросы входного сигнала с помощью идентификатора Хампеля. Этот Идентификатор Хампеля является изменением правила статистики с тремя сигмами, которое устойчиво против выбросов. Для каждой выборки входного сигнала блок вычисляет медиану окна, состоящего из текущей выборки и $\frac{L e n - 1}{2}$ смежные образцы на каждой стороне текущей выборки. Len - длина окна, заданная параметром Window length. Блок также оценивает стандартное отклонение каждой выборки относительно ее медианы окна с помощью медианного абсолютного отклонения. Если выборка отличается от медианы больше, чем порог, умноженный на стандартное отклонение, фильтр заменяет выборку на медиану. Для получения дополнительной информации см. «Алгоритмы».

Порты

Вход

расширить все

`x` - Вход данных
вектор | матрица

Блок принимает многоканальные входы, то есть m -by - n входы размера, где m ≥ 1 и n ≥ 1. m - количество выборок в каждой системе координат (канале), а n - количество каналов. Блок также принимает входы переменного размера. То есть можно изменить размер каждого входного канала во время симуляции. Однако количество каналов не может измениться.

Этот порт не называется, пока вы не выберете параметр Specify threshold from input port.

Типы данных: single | double

`T` - Порог
действительный скаляр, больший или равный 0

Порог для определения выбросов, заданное как действительный скаляр, больший или равный 0. Для получения информации о том, как этот параметр используется для обнаружения выбросов, см. Алгоритмы.

Зависимости

Этот порт появляется, когда вы выбираете параметр Specify threshold from input port.

Типы данных: single | double

Выход

расширить все

`y` - Отфильтрованный выход
вектор | матрица

Размер и тип данных этого выхода совпадают с размером и типом данных входа.

Этот порт не называется до тех пор, пока вы не установите флажок Output outlier status.

Типы данных: single | double

`outlier` - Вывод состояния выбросов
вектор | матрица

Значение 1 в этом выходе указывает, что соответствующий элемент во входе является выбросами. Этот выход имеет тот же размер что и вход.

Зависимости

Чтобы включить этот порт, установите флажок Output outlier status.

Типы данных: Boolean

Параметры

расширить все

Если параметр указан как настраиваемый, то можно изменить его значение во время симуляции.

`Window length` - Длина раздвижного окна
`11` (по умолчанию) | положительное нечетное скалярное целое число

Длина скользящего окна, заданная как положительное нечетное скалярное целое число. Окно конечной длины скользит по данным, и блок вычисляет медианное и медианное абсолютное отклонение данных в окне.

`Specify threshold from input port` - Флаг для задания порога
off (по умолчанию) | on

При установке этого флажка порог вводится через порт T. Когда вы снимаете этот флажок, порог задается в диалоговом окне блока посредством параметра Threshold for outlier detection (standard deviations).

`Threshold for outlier detection (standard deviations)` - Порог
3 (по умолчанию) | действительный скаляр, больший или равный 0

Настраиваемый: Да

Зависимости

Этот параметр появляется при снятии флажка Specify threshold from input port.

`Output outlier status` - Флаг для вывода состояния выбросов
off (по умолчанию) | on

Выберите этот параметр, чтобы вывести матрицу boolean значения, которые имеют тот же размер, что и вход. Каждый элемент в этой матрице указывает, является ли соответствующий элемент во входе выбросами. Значение 1 указывает на выбросы.

`Simulate using` - Тип выполняемой симуляции
`Interpreted execution` (по умолчанию) | `Code generation`

Interpreted execution
Симулируйте модель с помощью MATLAB^® интерпретатор. Эта опция сокращает время запуска и обеспечивает более высокую скорость симуляции, чем Code generation.
Code generation
Симулируйте модель с использованием сгенерированного кода C. Первый раз, когда вы запускаете симуляцию, Simulink^® генерирует код С для блока. Код С повторно используется для последующих симуляций, пока модель не меняется. Эта опция требует дополнительного времени запуска и имеет более медленную скорость симуляции, чем Interpreted execution.

Характеристики блоков

Типы данных	`double` \| `single`
Прямое сквозное соединение	`no`
Многомерные сигналы	`no`
Сигналы переменного размера	`yes`
Обнаружение пересечения нулем	`no`

Подробнее о

расширить все

Идентификатор Хампеля

Этот Идентификатор Хампеля является изменением правила статистики с тремя сигмами, которое устойчиво к выбросам.

Учитывая последовательность x 1, _x 2, x 3, .._., xn и скользящее окно k длины, задайте медиану «точка-точка» и оценки стандартного отклонения с помощью:

Локальная медиана - $m_{i} = median (x_{i - k}, x_{i - k + 1}, x_{i - k + 2}, \dots, x_{i}, \dots, x_{i + k - 2}, x_{i + k - 1}, x_{i + k})$
Стандартное отклонение - $σ_{i} = κ median (| x_{i - k} - m_{i} |, \dots, | x_{i + k} - m_{i} |),$ где $κ = \frac{1}{\sqrt{2} {erfc}^{- 1} (1 / 2)} \approx 1.4826$

Величина _σi / κ известна как медианное абсолютное отклонение (MAD).

Если выборочный _xi такой, что

$| x_{i} - m_{i} | > n_{σ} σ_{i}$

для заданного порога _nσ, затем Идентификатор Хампеля объявляет _xi выбросов и заменяет его на _mi. Если _nσ равно 0, то фильтр Хэмпела ведет себя как обычный медианный фильтр.

Алгоритмы

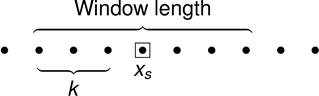
Для заданной выборки данных, _xs, алгоритм:

Центрирует окно нечетной длины в текущей выборке.
Вычисляет локальную медиану, _mi и стандартное отклонение, _σi, над активным окном данных.
Сравнивает текущую выборку с _nσ × _σi, где _nσ - пороговое значение. Если $| x_{s} - m_{i} | > n_{σ} \times σ_{i}$ фильтр идентифицирует текущую выборку, _xs, как выбросы и заменяют ее медианным значением, _mi.

Рассмотрим систему координат данных, которая передается в фильтр Хэмпеля.

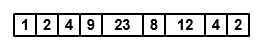
В этом примере фильтр Hampel скользит по данным окном длины 5 (Len). Фильтр имеет порог значение 2 (_nσ). Чтобы иметь полное окно в начале системы координат, алгоритм фильтра готовит систему координат с Len - 1 нулями. Чтобы вычислить первую выборку выхода, окно центрируется на ${[\frac{L e n - 1}{2} + 1]}^{th}$ выборка в добавленной системе координат, третий нуль в этом случае. Фильтр вычисляет медиану, среднее абсолютное отклонение и стандартное отклонение по данным в локальном окне.

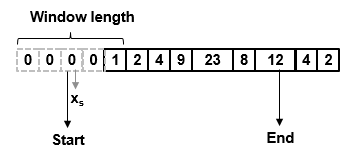
Текущая выборка: _xs = 0.
Окно данных: win = [0 0 0 0 1].
Локальная медиана: _mi = медиана ([0 0 0 0 1]) = 0.
Срединное абсолютное отклонение: $m a d_{i} = median (| x_{i - k} - m_{i} |, \dots, | x_{i + k} - m_{i} |)$ . Для этого окна данных, $m a d = median (| 0 - 0 |, \dots, | 1 - 0 |) = 0$ .
Стандартное отклонение: _σi = κ × _madi = 0, где $κ = \frac{1}{\sqrt{2} {erfc}^{- 1} (1 / 2)} \approx 1.4826$ .
Текущая выборка _xs = 0 не подчиняется отношению для определения выбросов.

$[| x_{s} - m_{i} | = 0] > [(n_{σ} \times σ_{i}) = 0]$
Поэтому фильтр Хэмпела выводит текущую входную выборку, _xs = 0.

Повторите эту процедуру для каждой последующей выборки, пока алгоритм не центрирует окно на ${[E n d - \frac{L e n - 1}{2}]}^{th}$ выборка, отмеченный как End. Потому что окно с центром на последнем $\frac{L e n - 1}{2}$ выборки не могут быть полными, эти выборки обрабатываются следующей системой координат входных данных.

Вот первый выходной кадр, который генерирует фильтр Хэмпеля:

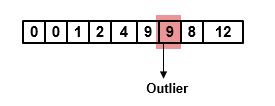
Седьмая выборка добавленного входного кадра 23 является выбросами. Фильтр Хэмпела заменяет эту выборку медианой над локальным окном [4 9 23 8 12].

Ссылки

[1] Боденем, Дин. «Адаптивная фильтрация и обнаружение изменений для потоковых данных». Доктор философии. Дипломная работа. Имперский колледж, Лондон, 2012.

[2] Лю, Ханьсун, Сириш Шах и Вэй Цзян. «Оперативное определение выбросов и очистка данных». Компьютеры и химическая техника. Том 28, 2004 марта, с. 1635-1647.

[3] Суомела, Юкка. Медианная фильтрация эквивалентна сортировке, 2014.

Документация

Hampel Filter

Описание

Порты