Метод скользящего окна и экспоненциальное взвешивание

Движущиеся объекты и блоки вычисляют статистику движения потоковых сигналов, используя один или оба из метода скользящего окна и экспоненциального метода взвешивания. Метод скользящего окна имеет конечную импульсную характеристику, в то время как метод экспоненциального взвешивания имеет бесконечную импульсную характеристику. Чтобы анализировать статистику за конечную длительность данных, используйте метод скользящего окна. Метод экспоненциального взвешивания требует меньшего количества коэффициентов и более подходит для встраиваемых приложений.

Объект, блок	Метод раздвижного окна	Экспоненциальный метод взвешивания
`dsp.MedianFilter`, Median Filter	✓
`dsp.MovingAverage`, Moving Average	✓	✓
`dsp.MovingMaximum`, Moving Maximum	✓
`dsp.MovingMinimum`, Moving Minimum	✓
`dsp.MovingRMS`, Moving RMS	✓	✓
`dsp.MovingStandardDeviation`, Moving Standard Deviation	✓	✓
`dsp.MovingVariance`, Moving Variance	✓	✓

Метод раздвижного окна

В методе раздвижного окна окно заданной длины, Len, перемещается по данным, выборке за выборкой, и статистика вычисляется по данным в окне. Выходом для каждой входной выборки является статистика над окном текущей выборки и Len - 1 предыдущей выборки. На первом этапе, чтобы вычислить первый Len - 1 выходы когда в окне еще не хватает данных, алгоритм заполняет окно нулями. В последующих временных шагах, чтобы заполнить окно, алгоритм использует выборки из предыдущей системы координат данных. Движущиеся статистические алгоритмы имеют состояние и запоминают предыдущие данные.

Рассмотрим пример вычисления скользящего среднего значения потоковых входных данных с помощью метода скользящего окна. Алгоритм использует длину окна 4. С каждой входной выборкой, которая поступает, окно длины 4 перемещается вдоль данных.

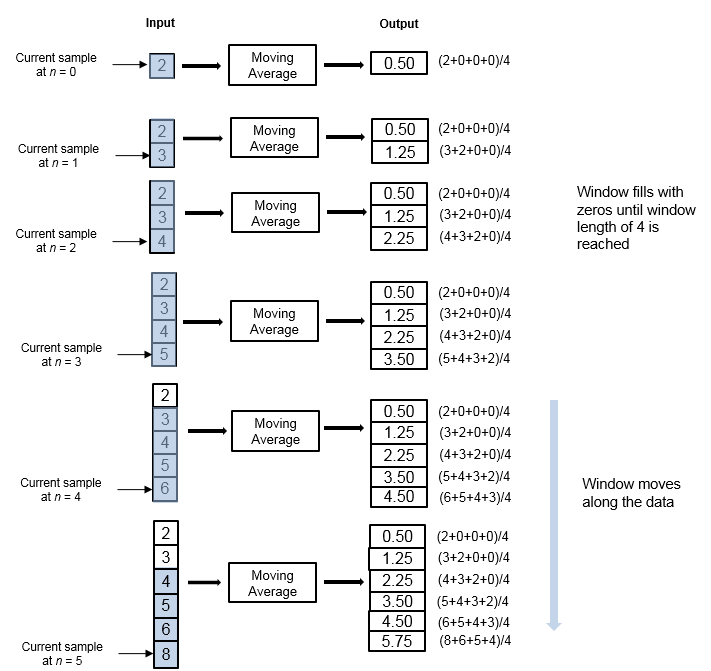
Окно имеет конечную длину, что делает алгоритм фильтром с конечной импульсной характеристикой. Чтобы анализировать статистику за конечную длительность данных, используйте метод скользящего окна.

Эффект длины окна

Длина окна определяет длину данных, над которыми алгоритм вычисляет статистику. Окно перемещается, когда поступают новые данные. Если окно большое, вычисленная статистическая величина ближе к стационарной статистике данных. Для данных, которые не изменяются быстро, используйте длинное окно, чтобы получить более плавную статистику. Для данных, которые изменяются быстро, используйте меньшее окно.

Экспоненциальный метод взвешивания

Экспоненциал взвешивания имеет бесконечную импульсную характеристику. Алгоритм вычисляет набор весов и применяет эти веса к выборкам данных рекурсивно. Когда возраст данных увеличивается, величина весового коэффициента уменьшается экспоненциально и никогда не достигает нуля. Другими словами, последние данные оказывают больше влияния на статистику в текущей выборке, чем более старые данные. Из-за бесконечной импульсной характеристики алгоритм требует меньшего количества коэффициентов, что делает его более подходящим для встраиваемых приложений.

Значение коэффициента забывания определяет скорость изменения коэффициентов взвешивания. Коэффициент забывания 0,9 дает больший вес старшим данным, чем коэффициент забывания 0,1. Чтобы придать больший вес недавним данным, отодвиньте коэффициент забывания ближе к 0. Для обнаружения небольших сдвигов в быстро изменяющихся данных более подходящим является меньшее значение (ниже 0,5). Коэффициент забывания 1,0 указывает на бесконечную память. Всем предыдущим выборкам придают одинаковый вес. Оптимальное значение коэффициента забывания зависит от потока данных. Для данного потока данных, чтобы вычислить оптимальное значение для коэффициента забывания, смотрите [1].

Рассмотрим пример вычисления скользящего среднего значения с помощью экспоненциального метода взвешивания. Коэффициент забывания составляет 0,9.

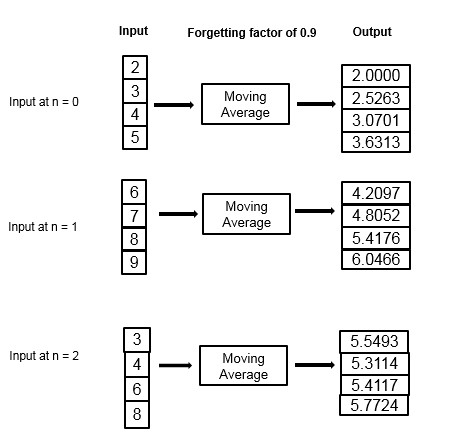
Алгоритм скользящего среднего обновляет вес и вычисляет скользящее среднее значение рекурсивно для каждой выборки данных, которая поступает с помощью следующих рекурсивных уравнений.

$\begin{array}{l} w_{N, λ} = λ w_{N - 1, λ} + 1 \\ {\bar{x}}_{N, λ} = (1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ} + (\frac{1}{w_{N, λ}}) x_{N} \end{array}$

.r- Коэффициент забывания.
$w_{N, λ}$ - Весовой коэффициент, примененный к текущей выборке данных.
$x_{N}$ - Входная выборка текущих данных.
${\bar{x}}_{N - 1, λ}$ - Скользящее среднее значение по предыдущей выборке.
$(1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ}$ - Эффект предыдущих данных на среднее значение.
${\bar{x}}_{N, λ}$ - Скользящее среднее значение в текущей выборке.

Данные	Вес $w_{N, λ} = λ w_{N - 1, λ} + 1$	Среднее значение ${\bar{x}}_{N, λ} = (1 - \frac{1}{w_{N, λ}}) {\bar{x}}_{N - 1, λ} + (\frac{1}{w_{N, λ}}) x_{N}$
Система координат 1
2	1. Для N = 1 это значение равняется 1.	2
3	0.9×1+1 = 1.9	(1– (1/1.9)) ×2 + (1/1.9) ×3 = 2.5263
4	0.9×1.9+1 = 2.71	(1– (1/2.71)) ×2.52 + (1/2.71) ×4 = 3.0701
5	0.9×2.71+1 = 3.439	(1– (1/3.439)) ×3.07 + (1/3.439) ×5 = 3.6313
Система координат 2
6	0.9×3.439+1 = 4.095	(1– (1/4.095)) ×3.6313 + (1/4.095) ×6 = 4.2097
7	0.9×4.095+1 = 4.6855	(1– (1/4.6855)) ×4.2097 + (1/4.6855) ×7 = 4.8052
8	0.9×4.6855+1 = 5.217	(1– (1/5.217)) ×4.8052 + (1/5.217) ×8 = 5.4176
9	0.9×5.217+1 = 5.6953	(1– (1/5.6953)) ×5.4176 + (1/5.6953) ×9 = 6.0466
Система координат 3
3	0.9×5.6953+1 = 6.1258	(1– (1/6.1258)) ×6.0466 + (1/6.1258) ×3 = 5.5493
4	0.9×6.1258+1 = 6.5132	(1– (1/6.5132)) ×5.5493 + (1/6.5132) ×4 = 5.3114
6	0.9×6.5132+1 = 6.8619	(1– (1/6.8619)) ×5.3114 + (1/6.8619) ×6 = 5.4117
8	0.9×6.8619+1 = 7.1751	(1– (1/7.1751)) ×5.4117 + (1/7.1751) ×8 = 5.7724

Алгоритм скользящего среднего имеет состояние и запоминает данные с предыдущего временного шага.

Для первой выборки, когда N = 1, алгоритм выбирает $w_{N, λ}$ = 1. Для следующей выборки весовой коэффициент обновляется, и среднее значение вычисляется с помощью рекурсивных уравнений.

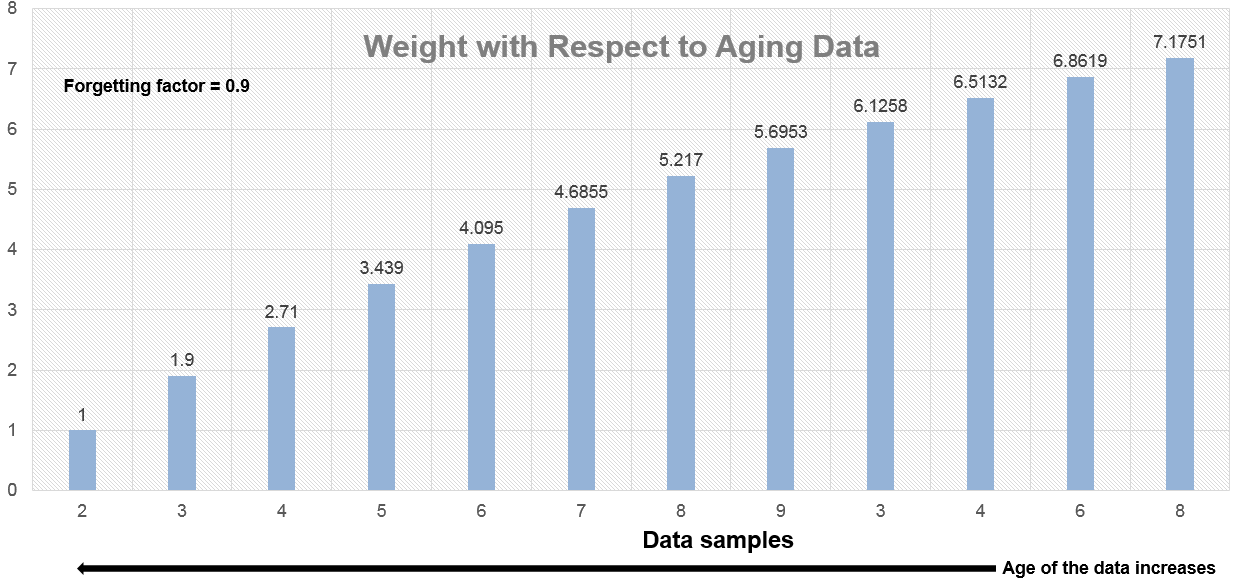
Когда возраст данных увеличивается, величина весового коэффициента уменьшается экспоненциально и никогда не достигает нуля. Другими словами, последние данные оказывают большее влияние на текущее среднее значение, чем более старые данные.

Когда коэффициент забывания равен 0,5, веса, применяемые к более старым данным, ниже, чем когда коэффициент забывания равен 0,9.

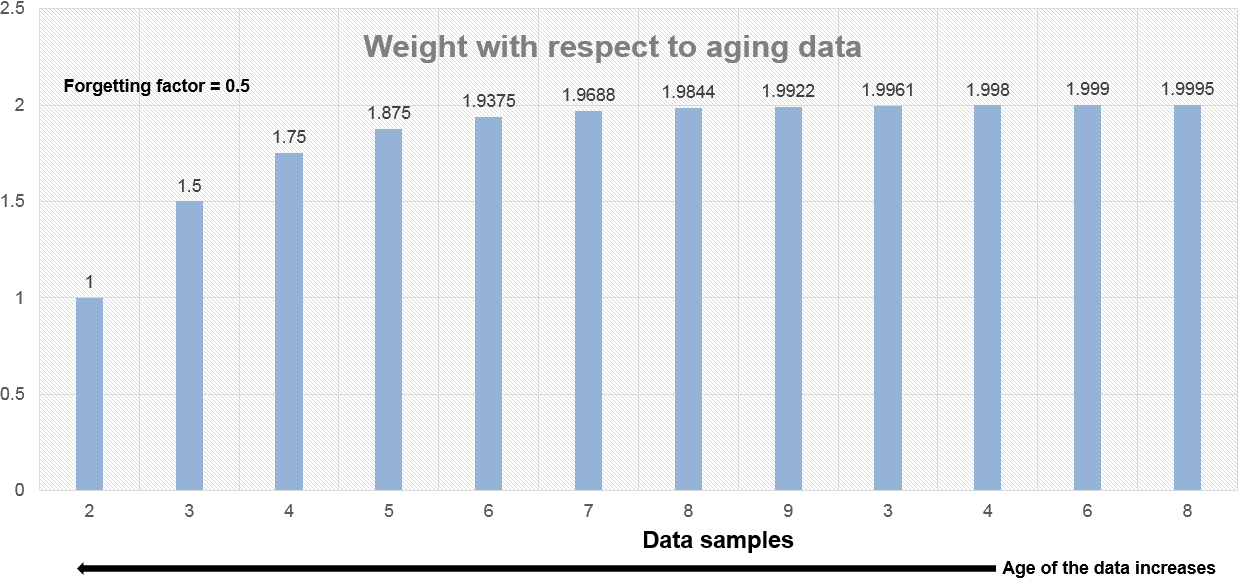
Когда коэффициент забывания равен 1, все выборки данных взвешиваются одинаково. В этом случае экспоненциально взвешенный метод аналогичен методу раздвижного окна с бесконечной длиной окна.

Когда сигнал изменяется быстро, используйте более низкий коэффициент забывания. Когда коэффициент забывания низкий, эффект прошлых данных меньше на текущее среднее значение. Это делает переходный процесс более острым. В качестве примера рассмотрим быстро изменяющийся шумный сигнал шага.

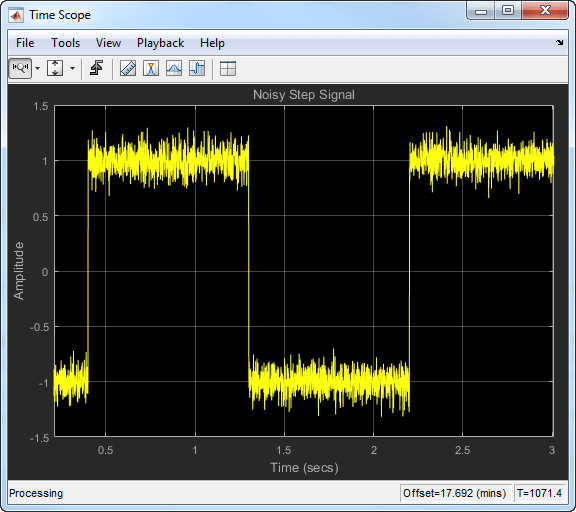
Вычислите скользящее среднее значение этого сигнала с помощью экспоненциально взвешенного метода. Сравните эффективность алгоритма с коэффициентами забывания 0,8, 0,9 и 0,99.

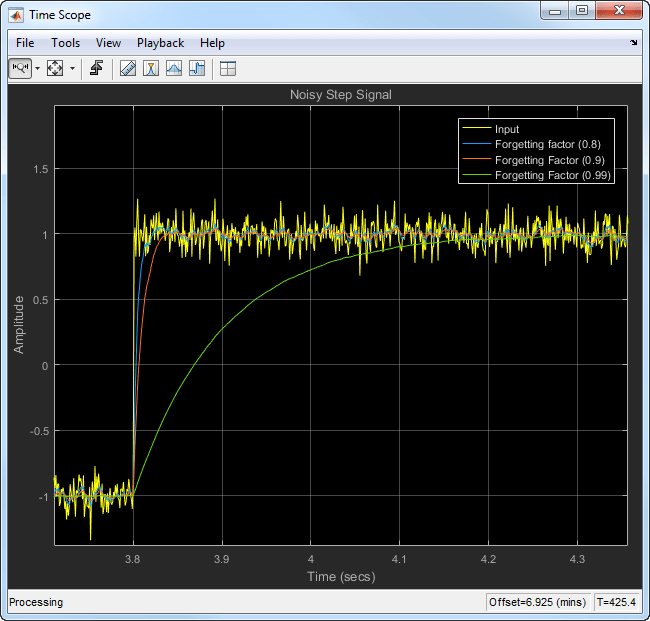
Когда вы масштабируете график, можно увидеть, что переходный процесс в движущемся среднем значении резок, когда коэффициент забывания низкий. Это делает его более подходящим для данных, которые изменяются быстро.

Для получения дополнительной информации об алгоритме скользящего среднего смотрите раздел Алгоритмы в dsp.MovingAverage Системная object™ или Moving Average блочная страница.

Для получения дополнительной информации о других движущихся статистических алгоритмах см. Раздел «Алгоритмы» в соответствующем системном объекте и страницах блоков.

Ссылки

[1] Боденем, Дин. «Адаптивная фильтрация и обнаружение изменений для потоковых данных». PH.D. Дипломная работа. Имперский колледж, Лондон, 2012.

Документация