В этом примере показано, как использовать скользящее окно, чтобы проверить, являются ли параметры модели timeseries инвариантными по времени. В этом примере анализируются два временных рядов:
Timeseries 1: моделируемые данные из известной, инвариантной по времени модели
Timeseries 2: моделируемые данные из известной, изменяющейся во времени модели
Полностью задайте эту модель AR (1) для Time-series 1 :
где является Гауссовым со средним 0 и отклонением 1. Полностью задайте эту изменяющуюся во времени модель для Time-series 2:
где является Гауссовым со средним 0 и отклонением 1.
Mdl1 = arima('AR',0.6,'Constant',0,'Variance',1); Mdl2 = cell(3,1); % Preallocate ARMdl2 = [0.2 0.75 -0.5]; for j = 1:3 Mdl2{j} = arima('AR',ARMdl2(j),'Constant',0,'Variance',1); end
Mdl1 является arima объекты модели. Вы можете получить доступ к его свойствам с помощью записи через точку. Mdl2 - массив ячеек из arima объекты модели. Можно индексировать камеры и запись через точку для доступа к свойствам моделей в Mdl2. Для примера получить доступ к AR- значения параметров третьей модели в Mdl3, введите Mdl2{3}.AR.
Моделируйте T = 200 периодов данных из Mdl1 и Mdl2. Используйте предварительный пример отклика 0 для обеих серий.
rng(1); % For reproducibility T = 200; y1 = simulate(Mdl1,T,'Y0',0); timeMdl2 = [100 50 50]; % Number of observations per model in Mdl2 y2 = 0; for k = 1:numel(Mdl2) y2 = [y2; simulate(Mdl2{k},timeMdl2(k),'Y0',y2(end))]; end Y = [y1 y2(2:end)];
Задайте пустые модели AR (1) для оценки Mdl1, Mdl2, и Mdl3. Оцените все три модели с помощью соответствующих наборов данных и размера окна качения 40 периодов. Кроме того, используйте шаг окна качения в один период. Сохраните авторегрессивные параметры и предполагаемое отклонение инноваций.
Mdl = arima('ARLags',1,'Constant',0); m = 100; % Rolling window size N = T - m + 1; % Number of rolling windows EstParams = cell(2,1); % Preallocate for estimates EstParamsMat = zeros(N,2); EstParamsSE = cell(2,1); EstParamsSEMat = zeros(N,2); for j = 1:2 for k = 1:N idxRW = k:(m + k - 1); % In-sample indices [EstMdl,EstParamCov] = estimate(Mdl,Y(idxRW,j),'Display','off'); EstParamsMat(k,:) = [EstMdl.AR{1} EstMdl.Variance]; EstParamsSEMat(k,:) = sqrt([EstParamCov(2,2) EstParamCov(3,3)]); end EstParams{j} = EstParamsMat; EstParamsSE{j} = EstParamsSEMat; end
Постройте график оценок и их точечных доверительных интервалов по индексу скользящего окна.
titleMdls = {'Mdl1','Mdl2'};
for j = 1:2
figure;
subplot(2,1,1);
Estimates = EstParams{j};
SEs = EstParamsSE{j};
plot(Estimates(:,1),'LineWidth',2);
hold on;
plot(Estimates(:,1) + 2*SEs(:,1),'r:','LineWidth',2);
plot(Estimates(:,1) - 2*SEs(:,1),'r:','LineWidth',2);
title(sprintf('%s - AR at Lag 1 Estimate',titleMdls{j}));
xlabel 'Rolling window index';
axis tight;
hold off;
subplot(2,1,2);
plot(Estimates(:,2),'LineWidth',2);
hold on;
plot(Estimates (:,2) + 2*SEs(:,2),'r:','LineWidth',2);
plot(Estimates(:,2) - 2*SEs(:,2),'r:','LineWidth',2);
title(sprintf('%s - Variance Estimate',titleMdls{j}));
xlabel 'Rolling window index';
axis tight;
hold off;
end

Для Mdl1оценка AR не сильно варьируется от 0,6, и оценки не значительно отличаются друг от друга (парно). Аналогичные результаты происходят для отклонения Mdl1. Оценка AR Mdl2 растет, а затем падает, что указывает на временную зависимость. Кроме того, на основе доверительных интервалов существуют доказательства того, что одни оценки отличаются от других. Хотя отклонение не изменилась во время симуляции, по-видимому, существует гетероскедастичность, возможно вызванная нестабильностью модели.
Этот пример показывает, как задать и оценить модель пространства состояний при проведении анализа окна качения на стабильность. Анализ окна качения для явно заданной модели пространства состояний прост, поэтому этот пример фокусируется на неявно заданных моделях пространства состояний.
Рассмотрим эту модель пространства состояний:
где εt и ut являются Гауссовым процессом со средним 0 и отклонением 1. Создайте функцию rwParamMap.m, который задает, как параметры в params сопоставить с матрицами модели пространства состояний, начальными значениями состояний и типом состояния и сохранить его в рабочей папке.
function [A,B,C,D,Mean0,Cov0,StateType,deflateY] = rwParamMap(params,y,Z) %rwParamMap Parameter-to-matrix mapping function for rolling window example %using ssm and specifying an AR(1) state model % The state space model specified by rwParamMap contains a stationary % AR(1) state, the observation model includes a regression component, and % the variances of the innovation and disturbances are 1. The response y % is deflated by the regression component specified by the predictor % variables x. A = params(1); B = 1; C = 1; D = 1; Mean0 = []; Cov0 = []; StateType = 0; deflateY = y - params(2)*Z; end
Программное обеспечение не поддерживает симуляцию неявных моделей, содержащих регрессионый компонент. Поэтому, чтобы симулировать данные из этой модели, необходимо задать все компоненты модели до компонента регрессии. Это можно сделать явным образом, поскольку в этом примере используется модель простого пространства состояний. В противном случае можно создать другую функцию и неявно задать другую модель пространства состояний (например, для изменяющихся во времени моделей пространства состояний).
Mdl2Sim = ssm(NaN,1,1,1,'StateType',1);Mdl2Sim является неявно заданным ssm объект.
Симулируйте 200-периодический путь случайных стандартных Гауссовых данных. Затем моделируйте ответы от Mdl2Sim, и надувать ответы регрессионным компонентом. В данном примере используйте ϕ = 0,6 и β = 2.
rng(1); % For reproducibility T = 200; Z = randn(T,1); phi = 0.6; beta = 2; deflateY = simulate(Mdl2Sim,T,'Params',phi); y = deflateY + Z*beta;
y - это надутый, симулированный отклик путь и Z - моделируемый ряд предикторов.
Если вы неявно задаете модель пространства состояний и данные отклика и предиктора (т.е. y и Z) существуют в MATLAB® Рабочая область, затем программное обеспечение создает ссылку из функции отображения параметра в матрицу, этой серии. Если данные не существуют в Рабочем пространстве MATLAB, то программное обеспечение создает модель, но вы должны предоставить данные с помощью соответствующих аргументов пары "имя-значение", когда вы, например, оцениваете модель.
Поэтому, чтобы провести анализ окна качения, когда модель пространства состояний неявно задана и существует регрессионый компонент, необходимо задать модель пространства состояний, указывающую индексы данных, которые будут анализироваться для каждого окна. Выполните анализ моделируемых данных в окне качения. Допустим длина окна качения будет 100 периодов для этого примера.
m = 100; N = T - m + 1; % Number of rolling windows EstParams = nan(N,2); % Preallocation EstParamSE = nan(N,2); for j = 1:N; idxRW = j:(m + j - 1); Mdl = ssm(@(c)rwParamMap(c,y(idxRW),Z(idxRW))); [~,EstParams(j,:),EstParamCov] = estimate(Mdl,y(idxRW),[0.5 1]',... 'Display','off'); EstParamSE(j,:) = sqrt(diag(EstParamCov)); end
Постройте график оценок и точечных доверительных интервалов для параметра AR и коэффициента регрессии.
figure; subplot(2,1,1); plot(EstParams(:,1),'LineWidth',2); hold on; plot(EstParams(:,1) + 2*EstParamSE(:,1),':r','LineWidth',2); plot(EstParams(:,1) - 2*EstParamSE(:,1),':r','LineWidth',2); title 'State AR Estimate at Lag 1'; xlabel 'Rolling window index'; axis tight; hold off; subplot(2,1,2); plot(EstParams(:,2),'LineWidth',2); hold on; plot(EstParams(:,2) + 2*EstParamSE(:,2),':r','LineWidth',2); plot(EstParams(:,2) - 2*EstParamSE(:,2),':r','LineWidth',2); title 'Regression Coefficient Estimate'; xlabel 'Rolling window index'; axis tight; hold off;
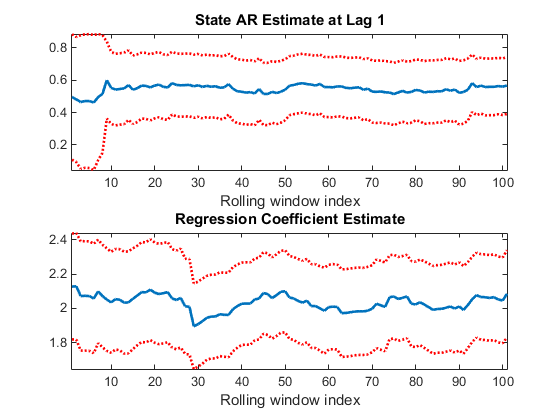
Графики указывают, что модель является стабильной, поскольку оценка AR не сильно отклоняется от ее среднего значения, также как и оценка коэффициента регрессии.