Оконный анализ моделей Timeseries

Анализ скользящего окна модели timeseries оценивает:

Стабильность модели с течением времени. Общим допущением модели timeseries является то, что коэффициенты постоянны относительно времени. Проверка на нестабильность составляет исследование, являются ли коэффициенты инвариантными по времени.
Точность прогноза модели.

Анализ устойчивости параметров в окне качения

Предположим, что у вас есть данные для всех периодов в выборке. Чтобы проверить стабильность модели timeseries с помощью окна качения:

Выберите размер окна качения, m, т.е. количество последовательных наблюдений за окном качения. Размер окна качения будет зависеть от размера, T и периодичности данных. В целом можно использовать короткий размер окна для данных, собранных в коротких интервалах, и больший размер для данных, собранных в более длинных интервалах. Более длинные размеры окна качения, как правило, дают более плавные оценки окна качения, чем более короткие размеры.
Предположим, что количество шагов между последовательными окнами качения составляет 1 период, затем разбейте весь набор данных на N = T - m + 1 подвыборки. Первое окно качения содержит наблюдения за периодом с 1 по m, второе окно качения содержит наблюдения за периодом с 2 по m + 1 и так далее.
Существуют изменения на разбиениях, например, вместо того, чтобы крен одно наблюдение вперед, можно прокрутить четыре наблюдения для ежеквартальных данных.
Оцените модель с помощью каждой подвыборки окна качения.
Постройте график каждой оценки и точечных доверительных интервалов (т.е., $\hat{θ} \pm 2 [\hat{S E} (\hat{θ})]$ ) над индексом окна качения, чтобы увидеть, как изменяется оценка со временем. Вы должны ожидать небольших колебаний для каждого, но большие колебания или тренды указывают на то, что параметр может быть изменяющимся во времени.

Для получения дополнительной информации об оценке устойчивости модели с помощью анализа окна качения, смотрите [1].

Анализ окна качения для прогнозирующей эффективности

Предположим, что у вас есть данные для всех периодов в выборке. Можно backtest проверить прогнозирующую эффективность нескольких моделей timeseries с помощью окна качения. На этих шагах описывается, как выполнить обратную проверку.

Выберите размер окна качения, m, т.е. количество последовательных наблюдений за окном качения. Размер окна качения зависит от размера, T и периодичности данных. В целом можно использовать короткий размер окна для данных, собранных в коротких интервалах, и больший размер для данных, собранных в более длинных интервалах. Более длинные размеры окна качения, как правило, дают более плавные оценки окна качения, чем более короткие размеры.
Выберите горизонт прогноза, h. Горизонт прогноза зависит от применения и периодичности данных. Ниже показано, как окно качения разделяет набор данных.
Если количество шагов между последовательными окнами качения составляет 1 период, то разбейте весь набор данных на N = T - m + 1 подвыборки. Первое окно качения содержит наблюдения за периодом с 1 по m, второе окно качения содержит наблюдения за периодом с 2 по m + 1 и так далее. Рисунок иллюстрирует разделы.

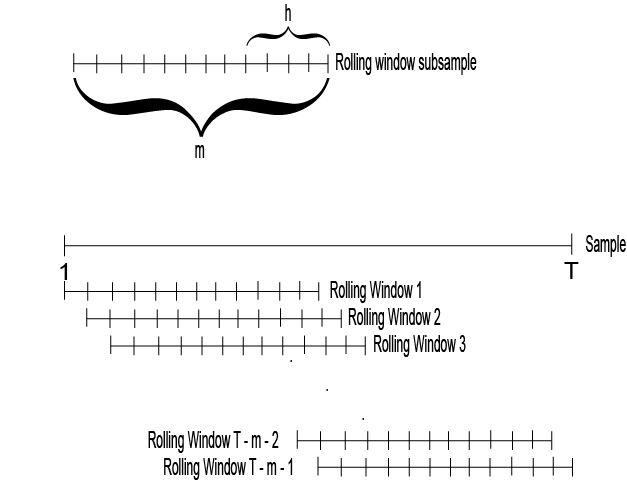
Существуют изменения на разбиениях, например, вместо того, чтобы крен одно наблюдение вперед, можно прокрутить четыре наблюдения для ежеквартальных данных.
Для каждой подвыборки окна качения:
1. Оцените каждую модель.
2. Оценка h -тепловые прогнозы.
3. Вычислите ошибки прогноза для каждого прогноза, то есть $e_{n j} = y_{m - h + n + j} - {\hat{y}}_{n j}$ , где:
  - _enj - ошибка прогноза n скользящего окна для прогноза j -step-award.
  - y - это ответ.
  - ${\hat{y}}_{n j}$ - j -теплового прогноза подвыборки окна качения n.
Вычислите корневые средние квадратичные невязки прогноза (RMSEs), используя ошибки прогноза для каждого типа прогноза с опережением. Другими словами,

$R M S E_{j} = \sqrt{\frac{\sum_{n = 1}^{N} e_{n j}^{2}}{n}} для j = 1, ..., h .$
Сравните RMSE среди моделей. Модель с самым низким набором RMSE имеет лучшую прогнозирующую эффективность.

Для получения дополнительной информации об обратном тестировании см. раздел [1].

Ссылки

[1] Zivot, E., and J. Wang. Моделирование финансовых временных рядов с S_PLUS®. 2nd ed. NY: Springer Science + Business Media, Inc., 2006.

Документация