Введение в методы назначения в системах отслеживания

Фон

В системе сопровождения нескольких целей (MTT) один или несколько датчиков генерируют несколько обнаружений от нескольких целей в скане. Чтобы отслеживать эти цели, одним из важных шагов является правильное назначение этих обнаружений целям или трекам, поддерживаемым в трекере, так что эти обнаружения могут использоваться для обновления этих треков. Если количество целей или обнаружений велико, или существуют конфликты между различными гипотезами назначения, назначение обнаружений является сложным.

В зависимости от размерности присвоения, задачи присвоения можно разделить на следующие категории:

2-D задания назначения - присваивает n цели m наблюдениям. Для примера присвойте 5 дорожек 6 обнаружениям, сгенерированным одним датчиком за один временной шаг.
Задача назначения S-D - присваивает n цели набору (m 1, _m 2, m 3,...) наблюдений. Например, присвойте 5 дорожек 6 обнаружениям от одного датчика и 4 обнаружениям от другого датчика одновременно. Этот пример является типичной задачей присвоения 3-D.

Чтобы проиллюстрировать основную идею задачи присвоения, рассмотрим простой пример 2-D присвоения. Одна компания пытается назначить 3 рабочих места 3 работникам. Из-за различных уровней опыта работников не все работники могут выполнить каждую работу с одинаковой эффективностью. Стоимость (в часах) каждого работника для завершения каждого задания определяется матрицей затрат, показанной в таблице. Правило назначения состоит в том, что каждый работник может взять только одно задание, а одно задание может быть занято только одним работником. Чтобы гарантировать эффективность, объект этого задания состоит в том, чтобы минимизировать общую стоимость.

Рабочий	Работа
Рабочий	1	2	3
1	41	72	39
2	22	29	49
3	27	39	60

Поскольку в этом примере количество рабочих и рабочих мест является маленьким, все возможные назначения могут быть получены путем перечисления, и решение с минимальными затратами подсвечивается в таблице с парами присвоения (1, 3), (2, 2) и (3, 1). На практике, когда размер назначения становится больше, оптимальное решение трудно получить для 2-D назначения. Для задачи S-D назначения оптимальное решение может быть не получено на практике.

2-D назначение при отслеживании нескольких целей

В 2-D задаче назначения MTT трекер пытается назначить несколько треков нескольким обнаружениям. Помимо задачи размерности, упомянутой выше, несколько других факторов могут значительно изменить сложность задания:

Цель или распределение обнаружения - если цели распределены редко, связать цель с соответствующим обнаружением относительно легко. Однако, если цели или обнаружения распределены плотно, назначения становятся неоднозначными, потому что назначение цели обнаружению или другому ближайшему обнаружению редко делает какие-либо различия в стоимости.
Вероятность обнаружения (P d) датчика - _P d описывает вероятность того, что цель обнаруживается датчиком, если цель находится в поле зрения датчика. Если P d датчика маленькая, то истинная цель может не вызвать никакого обнаружения во время скана датчика. В результате дорожка, представленная истинной целью, может красть обнаружения из других дорожек.
Разрешение датчика - Разрешение датчика определяет способность датчика отличать обнаружения от двух целей. Если разрешение датчика низкое, то две близкие цели могут вызвать только одно обнаружение. Это нарушает общее предположение, что каждое обнаружение может быть назначено только одной дорожке, и приводит к неразрешимым конфликтам назначения между дорожками.
Коэффициент загромождения или ложного предупреждения датчика - ложные предупреждения вводят дополнительные возможные назначения и, следовательно, увеличивают сложность назначения данных.

Сложность задачи назначения может определить, какие методы назначения применять. В Sensor Fusion and Tracking Toolbox™ toolbox используются три подхода к назначению 2-D, соответствующих трем различным трекерам:

trackerGNN - принимает глобальный подход к ближайшему присвоению данных
trackerJPDA - принимает совместный подход к ассоциации данных вероятностей
trackerTOMHT - принимает ориентированный на трекер подход отслеживания нескольких гипотез

Обратите внимание, что каждый трекер обрабатывает данные с датчиков последовательно, что означает, что каждый трекер занимается проблемой назначения только с обнаружениями одного датчика за раз. Даже при этом лечении может быть слишком много пар назначения. Чтобы уменьшить количество пар дорожки и обнаружения, рассматриваемых для назначения, часто используется метод стробирования.

Gating

Gating является механизмом скрининга, чтобы определить, какие наблюдения являются допустимыми кандидатами для обновления существующих треков и устранения маловероятных пар «обнаружение-отслеживание», используя информацию распределения предсказанных треков. Чтобы установить ворота валидации для дорожки на текущем скане, оценочная дорожка для текущего шага прогнозируется с предыдущего шага.

Для примера трекер подтверждает дорожку в момент t k и получает несколько обнаружений в момент времени _{t k} + 1. Чтобы сформировать ворота валидации в момент времени t k + 1, трекер сначала должен получить предсказанное измерение как:

${\hat{y}}_{k + 1} = h ({\hat{x}}_{k + 1 | k})$

где является оценкой дорожки, предсказанной из времени t _k и является моделью измерения, которая выводит ожидаемое измерение, заданное состояние дорожки. Вектор невязок наблюдения

$\tilde{y} = y_{k + 1} - {\hat{y}}_{k + 1}$

где y _k + 1 - фактическое измерение. Чтобы установить контур затвора, обнаружение остаточной ковариационной S используется для формирования эллипсоидального затвора валидации. Эллипсоидальные ворота, который устанавливает пространственную эллипсоидальную область в пространстве измерений, заданы в расстоянии Махаланобиса как:

$d^{2} (y_{k + 1}) = {\tilde{y}}^{T} S^{- 1} \tilde{y} \leq G$

где G - порог стробирования, который можно задать на основе требования к присвоению. Увеличение порога может включать больше обнаружений в затвор.

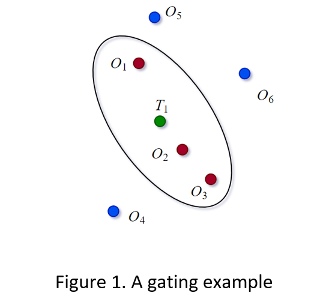
После того, как ворота назначения установлены для каждой дорожки, статус управления каждой y i обнаружения (i = 1,..., n) может быть определен путем сравнения его расстояния Махаланобиса d² (y i) с пороговым G стробирования. Если d² (y i) < G, затем обнаружение y i находится внутри ворот дорожки и будет рассмотрено на ассоциацию. В противном случае возможность обнаружения, связанная с дорожкой, удаляется. На фиг.1 _T 1 представляет предсказанную оценку дорожки, а O 1- O 6 являются шестью обнаружениями. На основе результатов стробирования, O 1, O 2 и O 3 находятся в пределах логики валидации на рисунке.

Глобальный метод ближайшего соседа (GNN)

Метод GNN является единичным методом назначения гипотез. Для каждого нового набора данных цель состоит в том, чтобы назначить глобальные ближайшие наблюдения существующим трекам и создать новые гипотезы о треках для неназначенных обнаружений.

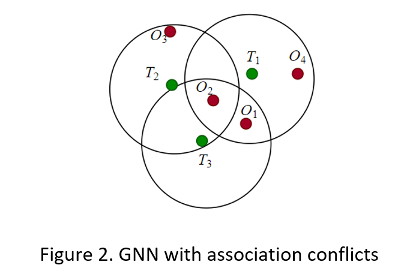
Задача назначения GNN может быть легко решена, если нет конфликтов ассоциации между треками. Трекеру нужно только назначить трек ближайшему соседу. Однако конфликтные ситуации (см. Фигуру 2) происходят, когда существует более одного наблюдения в пределах валидации ворот дорожки или наблюдение находится в воротах более чем одной дорожки. Чтобы разрешить эти конфликты, трекер должен оценить матрицу затрат.

Элементы массива матрицы затрат для метода GNN включают расстояние от треков до обнаружений и другие факторы, которые вы, возможно, захотите учесть. Для примера одним из подходов является определение обобщенного статистического расстояния между j наблюдения для отслеживания i как:

$C_{i j} = d_{i j} + \ln (| S_{i j} |)$

где d _ij - расстояние Махаланобиса и ln (_{|<reservedrangesplaceholder1><reservedrangesplaceholder0>|}), логарифм определяющего матрицы остаточных ковариаций, используется для наказания дорожек с большего предсказания неопределенностью.

Для задачи присвоения, представленной на фигуре 2, следующая таблица показывает гипотетическую матрицу затрат. Неотделенные присвоения, которые не прошли тест стробирования, обозначаются X. (На практике затраты на неотделенные присвоения могут быть обозначены большими значениями, такими как 1000.)

Следы	Наблюдения
Следы	<reservedrangesplaceholder0> 1	<reservedrangesplaceholder0> 2	<reservedrangesplaceholder0> 3	<reservedrangesplaceholder0> 4
<reservedrangesplaceholder0> 1	9	6	X	6
<reservedrangesplaceholder0> 2	X	3	10	X
<reservedrangesplaceholder0> 2	8	4	X	X

Для этой задачи подсвеченное оптимальное решение может быть найдено путем перечисления. Обнаружение O 3 не назначено, поэтому трекер будет использовать его для создания нового ориентировочного трека. Для более сложных задач назначения GNN требуются более точные формулировки и более эффективные алгоритмы для получения оптимального или неоптимального решения.

Общая задача назначения 2-D может быть сформирована следующим образом. Учитывая элемент матрицы затрат C _ij, найдите Z назначения = {_z ij}, которое минимизирует

$J = \sum_{i = 0}^{n} \sum_{j = 0}^{m} C_{i j} z_{i j}$

удовлетворяющее двум ограничениям:

$\begin{array}{l} \sum_{i = 0}^{m} z_{i j} = 1, \forall j \\ \sum_{j = 0}^{n} z_{i j} = 1, \forall i \end{array}$

Если i дорожки назначена j наблюдения, то z _ij = 1. В противном случае _z ij = 0. _z i 0 = 1 представляет гипотезу о том, что i дорожки не назначена никакому обнаружению. Точно так z 0 j = 1 представляет гипотезу, что j наблюдения не назначена ни одному треку. Первое ограничение означает, что каждое обнаружение может быть назначено не более чем одной дорожке. Второе ограничение означает, что каждая дорожка может быть назначена не более чем одному обнаружению.

Sensor Fusion and Tracking Toolbox обеспечивает несколько функций, чтобы решить 2-D задачи назначения GNN:

assignmunkres - Использует алгоритм Мункреса, который гарантирует оптимальное решение, но может потребовать больше операций вычисления.
assignauction - Использует алгоритм аукциона, который требует меньше операций, но может сходиться к оптимальному или неоптимальному решению.
assignjv - Использует алгоритм Джокера-Вольгенанта, который также сходится на оптимальном или неоптимальном решении, но обычно с более высокой скоростью сходимости.

В trackerGNNможно выбрать алгоритм назначения путем определения Assignment свойство.

K Лучшие Решения Задачи Назначения 2-D

Из-за неопределенности характера задач назначения, только получение решения (оптимального или неоптимального) может быть недостаточным. Для расчета нескольких гипотез о присвоении между треками и обнаружениями необходимо несколько неоптимальных решений. Эти неоптимальные решения называются K лучшими решениями задачи назначения.

K лучшие решения обычно получаются путем изменения решения, полученного любой из вышеупомянутых функций назначения. Затем, на следующем шаге, алгоритм K best solution удаляет одну пару track-to-detection в исходном решении и находит следующее лучшее решение. Для примера для этой матрицы затрат:

$[\begin{matrix} 10 & 5 & 8 & 9 \\ 7 & \times & 20 & \times \\ \begin{array}{l} \times \\ \times \end{array} & \begin{array}{l} 21 \\ 15 \end{array} & \begin{array}{l} \times \\ 17 \end{array} & \begin{array}{l} \times \\ \times \end{array} \\ \times & \times & 16 & 22 \end{matrix}]$

каждая строка представляет стоимость, связанную с дорожкой, а каждый столбец представляет стоимость, связанную с обнаружением. Как подсвечено, оптимальным решением является (7,15,16, 9) со стоимостью 47. На следующем шаге удалите первую пару (соответствующую 7), а следующее лучшее решение - (10,15, 20, 22) со стоимостью 67. После этого уберите вторую пару (соответствующую 15), а следующее лучшее решение - (7, 5,16, 9) со стоимостью 51. После нескольких шагов пять лучших решений:

Решение	Стоимость
(7,15,16, 9)	47
(7,5,17, 22)	51
(7,15, 8, 22)	52
(7, 21,16, 9)	53
(7, 21,17, 9)	53

Смотрите пример Найти пять лучших решений используя Assignkbest, который использует assignkbest функция для поиска K лучших решений.

Метод объединенной ассоциации данных вероятностей (JPDA)

В то время как метод GNN делает жесткое назначение обнаружения дорожке, метод JPDA применяет мягкое назначение, так что обнаружения в элементе валидации дорожки все могут вносить взвешенные вклады в дорожку на основе их вероятности ассоциации.

Например, для результатов стробирования, показанных на фиг.1, трекер JPDA вычисляет возможность связи между дорожкой T 1 и наблюдениями _O 1, O 2 и O 3. Предположим, что вероятность ассоциации этих трех наблюдений составляет p ₁₁, p 12 _и p 13, и их невязки относительно _{дорожки} T 1 равны, и, соответственно. Тогда взвешенная сумма невязок, сопоставленной с T 1 дорожки, является:

${\tilde{y}}_{1} = \sum_{j = 1}^{3} p_{1 j} {\tilde{y}}_{1 j}$

В трекере взвешенная невязка используется для обновления T дорожки 1 на шаге коррекции фильтра отслеживания. В фильтре вероятность отмены назначения, _p 10, также требуется для обновления отслеживания T 1. Для получения дополнительной информации смотрите Алгоритм коррекции JPDA для дискретного расширенного фильтра Калмана.

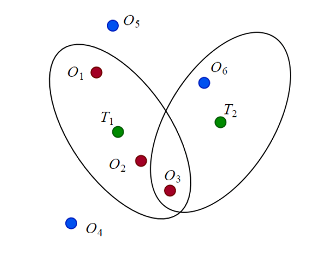
Метод JPDA требует еще одного шага, когда существуют конфликты между назначениями в разных треках. Например, на следующем рисунке дорожка T 2 конфликтует с _T 1 о присвоении O 3 наблюдения. Поэтому, чтобы вычислить вероятность ассоциации p 13, совместная вероятность того, что T 2 не назначена O 3 (то есть T 2 назначена O 6 или не назначена), должна быть рассчитана.

Метод отслеживания нескольких гипотез (TOMHT)

В отличие от метода JPDA, который объединяет все обнаружения в элементе валидации с помощью взвешенной суммы, метод TOMHT генерирует несколько гипотез или ветвей дорожек на основе обнаружений в элементе и распространяет высокоправдоподобные ветви между этапами скана. После распространения эти гипотезы могут быть проверены и сокращены на основе нового набора обнаружений.

Для примера для сценария стробирования, показанного в Фигуру 1, трекер TOMHT рассматривает следующие четыре гипотезы:

Не назначьте обнаружение T 1 приводя к гипотезе _T 10
Присвоение O 1 к _T 1, приводя к гипотезе _T 11
Присвоение O 2 к _T 1, приводя к гипотезе _T 12
Присвоение O 3 к _T 1, приводя к гипотезе _T 13

Учитывая порог назначения, трекер будет вычислять возможность каждой гипотезы и отбрасывать гипотезы с вероятностью ниже порога. Гипотетически, если только p ₁₀ и _p 11 больше порога, то только _T 10 и T 11 распространяются на следующий шаг для обновления обнаружения.

Назначение S-D при отслеживании нескольких целей

В задаче присвоения S-D размерность присвоения S больше 2. Обратите внимание, что все три трекера (trackerGNN, trackerJPDA, и trackerTOMHT) последовательно обрабатывают обнаружения от каждого датчика, что приводит к задаче назначения 2-D. Однако некоторые приложения требуют трекера, который обрабатывает одновременные наблюдения с нескольких сканов датчика все сразу, что требует решения задачи назначения S-D. Между тем, назначение S-D широко используется в приложениях отслеживания, таких как слияние статических данных, которое предварительно обрабатывает данные обнаружения перед подачей на трекер.

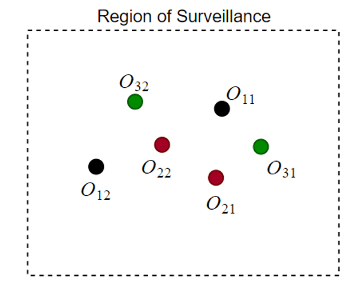
Задача назначения S-D для статического слияния данных имеет S сканы области наблюдения от нескольких датчиков одновременно, и каждое сканирование состоит из нескольких обнаружений. Источниками обнаружения могут быть реальные цели или ложные предупреждения. Объект состоит в том, чтобы обнаружить неизвестное количество целей и оценить их состояния. Для примера, как показано на Фигуре 4, три датчика сканов произвести шесть обнаружений. Обнаружение того же цвета относится к одному и тому же скану. Поскольку каждый скан генерирует два обнаружения, вероятно, в области наблюдения есть две цели. Чтобы выбрать между различными возможностями присвоения или связи, вычислите матрицу затрат.

Вычисление стоимости может зависеть от многих факторов, таких как расстояние между обнаружениями и ковариационное распределение каждого обнаружения. Чтобы проиллюстрировать базовую концепцию, затраты на присвоение для нескольких гипотез гипотетически приведены в таблице [1].

Гипотезы назначения	Наблюдения первого Скана (O _1x )	Наблюдение Скана (O _2x )	Третий Скан наблюдение (O _3x )	Стоимость
1	0	1	1	−10.2
2	1	2	0	−10.9
3	1	1	1	−18.0
4	1	1	2	−14.8
5	1	2	1	−17.0
6	2	0	1	−13.2
7	2	0	2	−10.6
8	2	2	0	−11.1
9	2	1	2	−14.1
10	2	2	2	−16.7

В таблице 0 обозначает дорожку, связанную без обнаружения в этом скане. Предположим, что гипотезы, не показанные в таблице, усекаются стробированием или игнорируются из-за высоких затрат. Чтобы кратко представлять каждую дорожку, используйте c _ijk, чтобы представлять стоимость для ассоциации i наблюдений в скане 1, j в скане 2 и k в скане 3. Для примера, для гипотезы о присвоении 1, _{c 011} = -10.2. Несколько гипотез трека конфликтуют с другими в таблице. Например, два наиболее вероятных назначения, _c 111 и _c 121, несовместимы, потому что они имеют одно и то же наблюдение в сканированиях 1 и 3.

Цель решения задачи назначения S-D состоит в том, чтобы найти наиболее вероятно совместимую гипотезу назначения с учетом всех обнаружений. Однако, когда S ≥ 3, известно, что задача масштабируется с количеством дорожек и обнаружений с экспоненциальной скоростью (NP-hard). Метод релаксации Лагранжа обычно используется, чтобы получить оптимальное или неоптимальное решение для задачи S-D назначения эффективно.

Краткое описание метода релаксации Лагранжа для назначения 3-D

Три сканирования данных имеют количество M 1, _M 2 и M 3 наблюдения, соответственно. Обозначим наблюдения скана 1, 2 и 3 как i, j и k, соответственно. Например, i = 1, 2,.._., M 1. _{Используйте} z ijk, чтобы представлять гипотезу формирования дорожки _O1 i, O ₂j и O 3 k. Если гипотеза верна, то z ijk = 1; _{в противном случае} z ijk = 0. Как _{уже упоминалось}, c ijk используется для представления стоимости z ijk _{ассоциации}. c ijk 0 для ложных предупреждений и отрицательно для возможных ассоциаций. Задача оптимизации S-D может быть сформулирована как:

$J (z) = \min_{i, j, k} \sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} \sum_{k = 0}^{M_{3}} c_{i j k} z_{i j k}$

с учетом трех ограничений:

$\begin{array}{l} \sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} z_{i j k} = 1, \forall k = 1, 2, \dots, M_{3} \\ \sum_{i = 0}^{M_{1}} \sum_{k = 0}^{M_{3}} z_{i j k} = 1, \forall j = 1, 2, \dots, M_{2} \\ \sum_{j = 0}^{M_{2}} \sum_{k = 0}^{M_{3}} z_{i j k} = 1, \forall i = 1, 2, \dots, M_{1} \end{array}$

Оптимизационная функция выбирает ассоциации, чтобы минимизировать общие затраты. Три ограничения гарантируют, что каждое обнаружение учитывается (включено в назначение или рассматривается как ложное предупреждение).

Метод релаксации Лагранжа приближается к этой задаче присвоения 3-D, ослабляя первое ограничение с помощью множителей Лагранжа. Задайте новую L функции (λ):

$L (λ) = \sum_{k = 0}^{M_{3}} λ_{k} [\sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} z_{i j k} - 1]$

где λ k, k = 1, 2,..., M 3 являются множителями Лагранжа. Вычесть L из исходной функции объекта J (z), чтобы получить новую функцию объекта, и первое ограничение в k ослаблено. Поэтому задача присвоения 3-D сводится к задаче присвоения 2-D, которая может быть решена любым из методов присвоения 2-D. Для получения дополнительной информации см. раздел [1].

Метод релаксации Лагранжа позволяет мягко нарушать первое ограничение, а потому может только гарантировать неоптимальное решение. Однако для большинства приложений этого достаточно. Чтобы задать точность решения, метод использует погрешность решения, которая определяет различие между текущим решением и потенциально оптимистичным решением. Погрешность неотрицательна, и меньшая погрешность решения соответствует решению ближе к оптимальному решению.

Sensor Fusion and Tracking Toolbox обеспечивает assignsd решить для назначения S-D с помощью метода Лагрангианской релаксации. Аналогично решателю K наилучшего 2-D назначения assignkbest, тулбокс также обеспечивает K лучший решатель назначения S-D, assignkbestsd, который используется для предоставления нескольких неоптимальных решений для задачи назначения S-D.

Смотрите Отслеживание с использованием распределенных синхронных пассивных датчиков для применения назначения S-D в статическом слиянии обнаружения.

См. также

Ссылки

[1] Блэкмен, С. и Р. Пополи. Проект и анализ современных систем слежения. Artech House Radar Library, Бостон, 1999.

[2] Мусицки, Д. и Р. Эванс. Joint Integrated Probabilistic Data Association: JIPDA (неопр.) (недоступная ссылка). Транзакции IEEE по аэрокосмическим и электронным системам. Том 40, № 3, 2004, стр 1093 -1099.

Документация