Нечеткий вывод - это процесс формулировки отображения от заданного входа до выхода с использованием нечеткой логики. Затем отображение предоставляет базис, из которого можно принимать решения или различать шаблоны. Процесс нечеткого вывода включает все части, которые описаны в Membership Functions, Logical Operations и If-Then Rules.
В этом разделе описывается процесс нечеткого вывода и используется пример задачи расчета чаевых с двумя входами, одним выходом и тремя правилами из The Базовой задачи расчета чаевых. Система нечеткого вывода для этой задачи принимает обслуживание и качество пищи в качестве входов и вычисляет процент советов с помощью следующих правил.
Если сервис плохой, или еда - тухлая, то чаевые будут маленькими.
Если сервис хороший, то чаевые средние.
Если сервис превосходен, или еда восхитительна, тогда чаевые будут большими
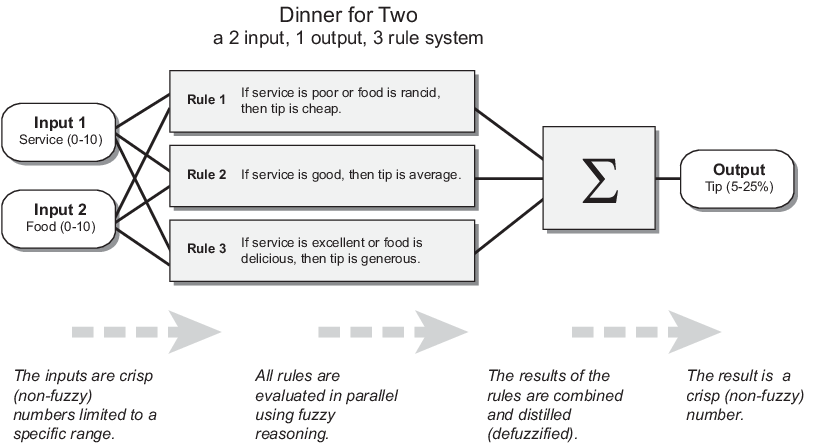
Параллельный характер правил является важным аспектом нечетких логических систем. Вместо резкого переключения между режимами, основанными на точках останова, логика плавно вытекает из областей, где доминирует то или иное правило.
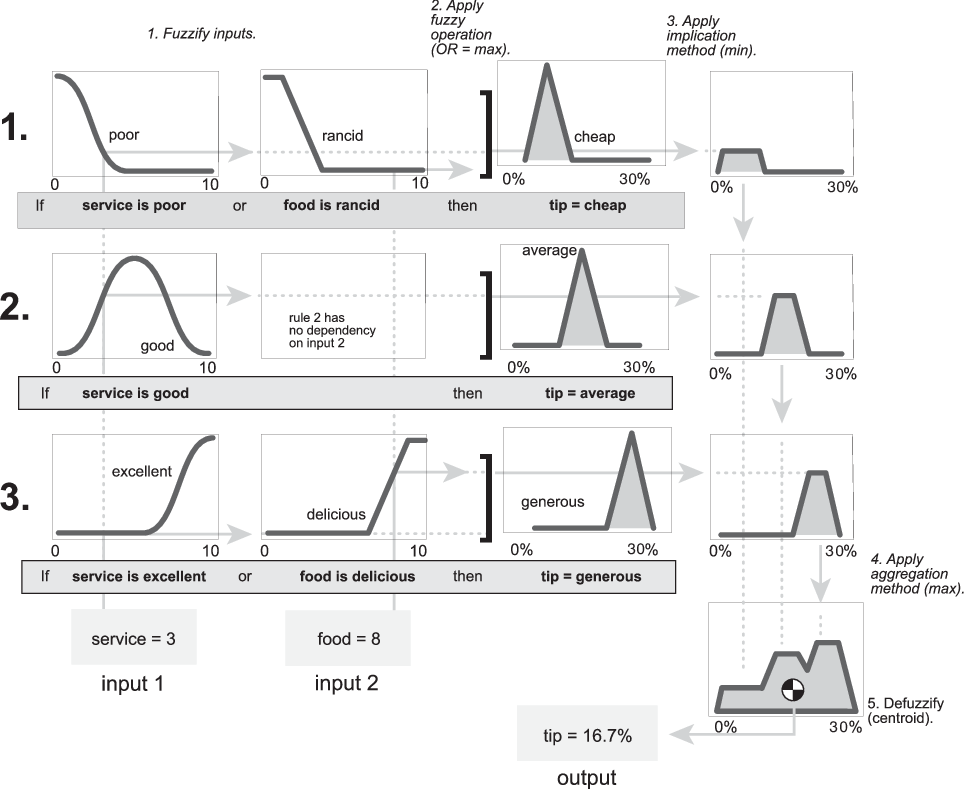
Процесс нечеткого вывода имеет следующие шаги.
Схема нечеткого вывода отображает все части процесса нечеткого вывода - от нечеткости до дефаззификации.
Первый шаг состоит в том, чтобы взять входы и определить степень их принадлежности к каждому из соответствующих нечетких наборов с помощью функций принадлежности (fuzzification). В программном обеспечении Fuzzy Logic Toolbox™ вход всегда является четким числовым значением, ограниченным вселенной дискурса входной переменной (в этом случае интервал от 0 до 10). Выходы являются нечеткой степенью принадлежности к определяющему языковому набору (всегда интервал от 0 до 1). Нечеткость входов определяется либо поиском по таблице, либо вычислением функции.
Этот пример построен на трех правилах, и каждый из правил зависит от разрешения входов в несколько различных нечетких языковых наборов: сервис плох, сервис хорош, еда - тухлая, еда восхитительна и так далее. Прежде чем правила могут быть оценены, входы должны быть нечеткими в соответствии с каждым из этих языковых наборов. Для примера, в какой степени еда восхитительна? Следующий рисунок показывает, насколько хорошо еда в гипотетическом ресторане (оценивается по шкале от 0 до 10) классифицируется как лингвистическая переменная, вкусная с помощью функции принадлежности. В этом случае мы оцениваем еду как 8, что, учитывая графическое определение вкусной, соответствует µ = 0,7 для вкусной функции членства.
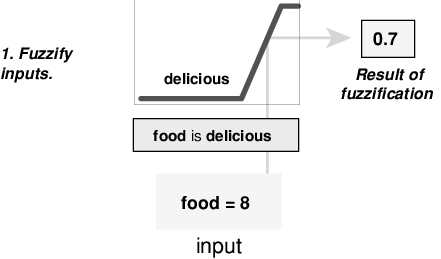
Таким образом, каждый вход нечеткий по всем определяющим функциям членства, требуемым правилами.
После того, как входы будут нечеткими, вы знаете, в какой степени каждая часть предшествующего элемента удовлетворяется для каждого правила. Если предшествующий элемент правила имеет более чем одну часть, нечеткий оператор применяется, чтобы получить одно число, которое представляет результат предшествующего правила. Затем это число применяется к выходной функции. Вход нечеткого оператора является двумя или более значениями принадлежности от нечетких входных переменных. Выходные выходы - одно значение истинности.
Как описано в Логических операциях, любое количество четко определенных методов может заполнить для операции И или операции ИЛИ. В тулбоксе поддерживаются два встроенных метода AND: min (минимум) и prod (продукт). Также поддерживаются два встроенных метода OR: max (максимум) и probor (вероятностный OR). Вероятностный метод OR (также известный как алгебраическая сумма) вычисляется согласно уравнению:
| probor (a, b) = a + b - ab |
В дополнение к этим встроенным методам можно создать свои собственные методы для AND и OR, написав любую функцию и установив, что будет вашим методом выбора. Для получения дополнительной информации см. «Создание нечетких систем с использованием пользовательских функций».
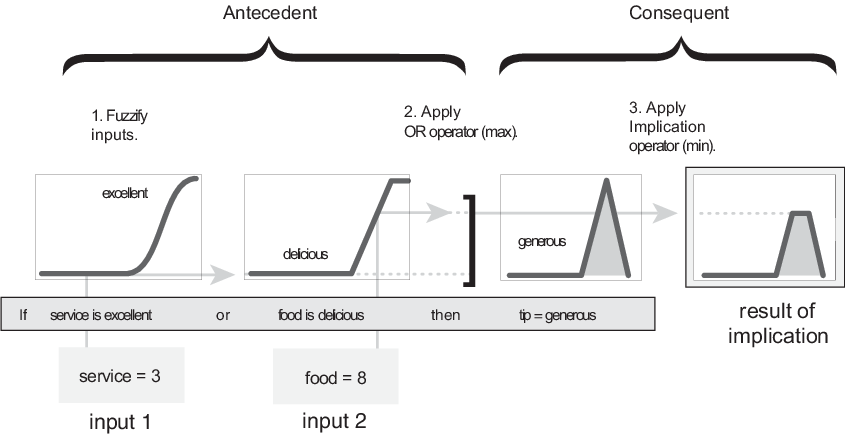
Следующий рисунок демонстрирует оператор OR max путем оценки предшествующего значения третьего правила вычисления чаевых. Для заданных рейтингов услуг и продуктов питания два элемента предшествующего (сервис превосходен, а еда восхитительна) производят нечеткие значения принадлежности 0,0 и 0,7, соответственно. Оператор fuzzy OR выбирает максимальное из двух значений, 0,7. Вероятностный метод OR все еще приводит к 0,7.
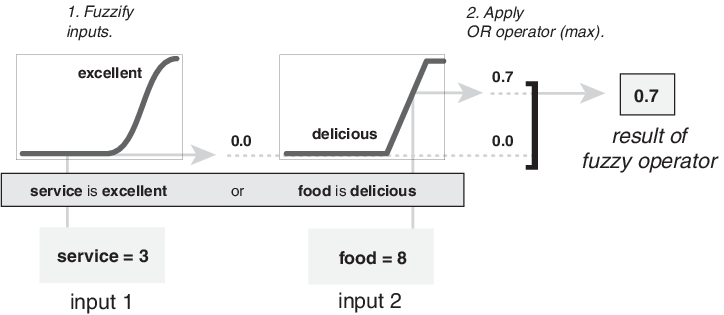
Перед применением метода implication необходимо определить вес правила. Каждое правило имеет вес (число от 0 до 1), который применяется к числу, заданному предшествующим. Обычно этот вес равен 1 (как и в данном примере) и, таким образом, не влияет на импликационный процесс. Однако можно уменьшить эффект одного правила относительно других, изменив его значение веса на что-то отличное от 1.
После того, как каждому правилу присвоено надлежащее взвешивание, реализуется метод implication. Следствием является нечеткое множество, представленное функцией принадлежности, которая надлежащим образом взвешивает языковые характеристики, которые ей приписываются. Последующее изменяется с помощью функции, сопоставленной с предшествующим числом (одно число). Вход для процесса импликации является одним числом, заданным предшествующим, и выход является нечетким множеством. Значение реализуется для каждого правила. Поддерживаются два встроенных метода, и они являются теми же функциями, которые используются методом AND: min (минимум), который обрезает выход нечеткий набор, и prod (продукт), который масштабирует выход нечеткий набор.
Примечание
Системы Sugeno всегда используют метод отражения продукта.
Поскольку решения основаны на проверке всех правил в FIS, выходы правил должны быть объединены определенным образом. Агрегация - это процесс, посредством которого нечеткие множества, которые представляют выходы каждого правила, объединяются в один нечеткий набор. Агрегация происходит только один раз для каждой выходной переменной, которая находится перед конечным шагом дефаззификации. Вход процесса агрегирования является список усеченных выходных функций, возвращаемых процессом импликации для каждого правила. Выходы процесса агрегации являются одним нечетким множеством для каждой выходной переменной.
Пока метод агрегации коммутативен, то порядок, в котором выполняются правила, неважен. Поддерживаются три встроенных метода.
max (максимум)
probor (вероятностный OR)
sum (сумма выходных наборов правил)
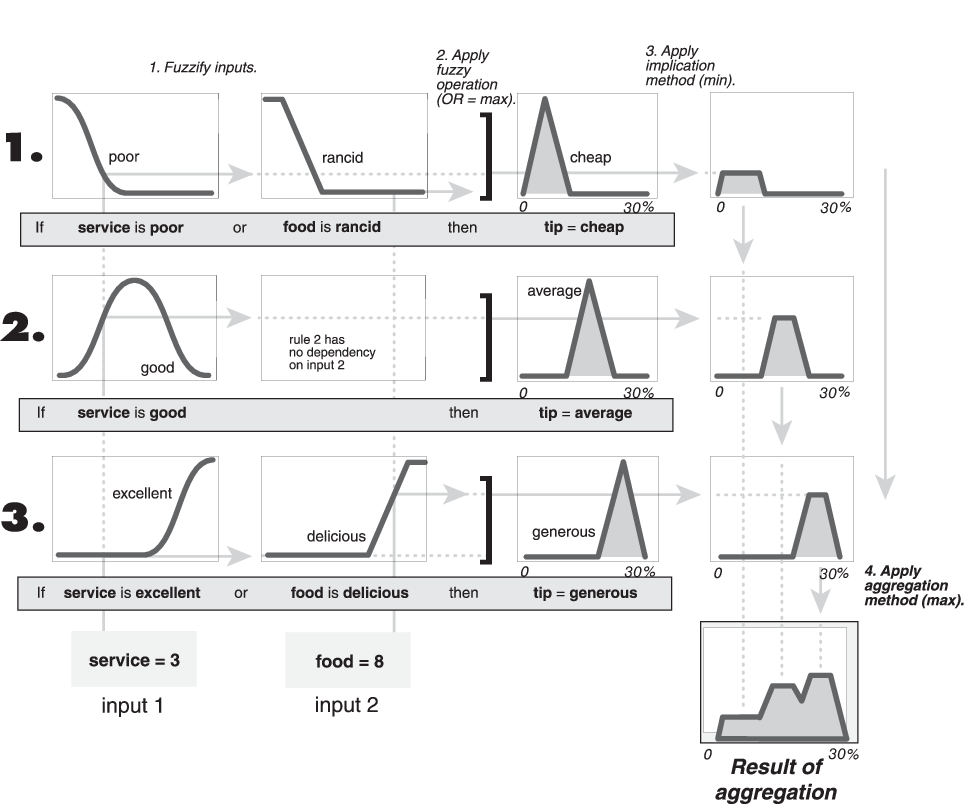
На следующей схеме все три правила отображаются, чтобы показать, как выходы правил агрегируются в один нечеткий набор, функция принадлежности которого присваивает взвешивание для каждого выхода (совета) значения.
Примечание
Системы Sugeno всегда используют sum метод агрегирования.
Вход для процесса дефаззификации является совокупным выходом нечеткого набора, и выход является одним числом. Поскольку нечеткость помогает оценке правила во время промежуточных шагов, конечным желаемым выходом для каждой переменной является обычно одно число. Однако совокупность нечеткого множества охватывает область значений выхода значений, и поэтому должна быть дефузифицирована, чтобы получить один выход значение из множества.
Поддерживаются пять встроенных методов дефаззификации: центроид, биссектор, середина максимума (среднее значение максимального значения выходного набора), наибольшее из максимума и наименьшее из максимума. Пожалуй, самым популярным методом дефаззификации является вычисление центроида, которое возвращает центр области под совокупным нечетким набором, как показано на следующем рисунке.
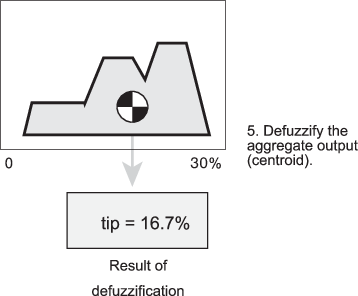
В то время как совокупный выходной нечеткий набор охватывает область значений от 0%, хотя и 30%, значение дефузификации находится между 5% и 25%. Эти пределы соответствуют центроидам cheap и generous функции членства, соответственно.
Схема нечеткого вывода является составной частью всех небольших схем, представленных до настоящего времени в этом разделе. Он одновременно отображает все части процесса нечеткого вывода, который вы исследовали. Информация течет через схему нечеткого вывода, как показано на следующем рисунке.
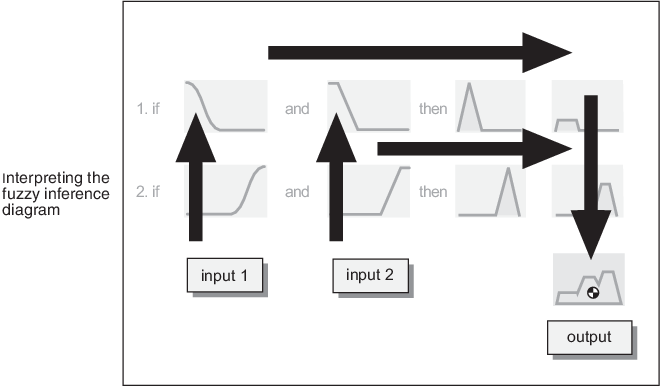
На этом рисунке поток вытекает из входов внизу слева, через каждую строку, а затем вниз по выходам правила внизу справа. Этот компактный поток показывает все сразу, от лингвистической переменной нечеткости весь путь через дефаззификацию совокупного выхода.
Следующий рисунок показывает фактическую полноразмерную нечеткую схему вывода для базовой задачи расчета чаевых. Используя диаграмму нечеткого вывода, можно многое узнать о том, как работает система. Например, для конкретных входов в этой схеме можно увидеть, что метод implication является усечением с функцией min. Функция max используется для операции нечеткого ИЛИ. Правило 3 (самая нижняя строка в схеме, показанной ранее) оказывает самое сильное влияние на выход. Rule Viewer, описанный в The Rule Viewer, является реализацией нечеткой схемы вывода.