Уточнение начальных точек

Сведения об уточнении начальных точек

Если некоторые компоненты вашей задачи не ограничены, GlobalSearch и MultiStart используйте искусственные границы, чтобы генерировать случайные начальные точки равномерно в каждом компоненте. Однако, если ваша проблема имеет дальние минимумы, вам нужны широко рассредоточенные стартовые точки, чтобы найти эти минимумы.

Используйте эти методы для получения широко диспергированных начальных точек:

Дайте широко разделенные границы в вашем problem структура.
Использование RandomStartPointSet объект со MultiStart алгоритм. Установите большое значение ArtificialBound свойство в RandomStartPointSet объект.
Использование CustomStartPointSet объект со MultiStart алгоритм. Используйте широко рассредоточенные стартовые точки.

Существуют преимущества и недостатки каждого способа.

Метод	Преимущества	Недостатки
Задайте границы в `problem`	Автоматическая генерация точек	Делает более сложным Гессиан
	Может использоваться с `GlobalSearch`	Неясно, как большие для установки границ
	Легкий для того чтобы сделать	Изменения `problem`
	Границы могут быть асимметричными	Только равномерные точки
Большие `ArtificialBound` в `RandomStartPointSet`	Автоматическая генерация точек	`MultiStart` только
	Не меняется `problem`	Только симметричные, равномерные точки
	Легкий для того чтобы сделать	Неясно, насколько велики `ArtificialBound`
`CustomStartPointSet`	Настраиваемый	`MultiStart` только
`CustomStartPointSet`	Не меняется `problem`	Требует программирования для генерации точек

Методы генерации начальных точек

Равномерная сетка
Возмущенная сетка
Широко рассредоточенные точки для компонентов без ограничений

Равномерная сетка

Чтобы сгенерировать равномерную сетку начальных точек:

Сгенерируйте многомерные массивы с ndgrid. Задайте нижнюю границу, интервалы и верхнюю границу для каждого компонента.
Например, чтобы сгенерировать набор трехмерных массивов с
- Первый компонент от -2 до 0, интервал 0,5
- Второй компонент от 0 до 2, интервал 0,25
- Третий компонент от -10 до 5, интервал 1
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
```
Поместите массивы в одну матрицу с каждой строкой, представляющей одну начальную точку. Для примера:
```
W = [X(:),Y(:),Z(:)];
```
В этом примере W является матрицей 720 на 3.
Поместите матрицу в CustomStartPointSet объект. Для примера:
```
custpts = CustomStartPointSet(W);
```

Звонить run с CustomStartPointSet объект как третий вход. Для примера,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Возмущенная сетка

Целочисленные стартовые точки могут привести к менее устойчивым решениям, чем слегка возмущенные стартовые точки.

Чтобы получить возмущенный набор начальных точек:

Сгенерируйте матрицу начальных точек как на шагах 1-2 Uniform Grid.
Возмущение начальных точек путем добавления случайной нормальной матрицы со средней 0 и относительно малым отклонением.
Для примера в Uniform Grid, после создания W матрица, добавьте возмущение:
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
W = [X(:),Y(:),Z(:)];
W = W + 0.01*randn(size(W));
```
Поместите матрицу в CustomStartPointSet объект. Для примера:
```
custpts = CustomStartPointSet(W);
```

Звонить run с CustomStartPointSet объект как третий вход. Для примера,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Широко рассредоточенные точки для компонентов без ограничений

В некоторых компонентах вашей задачи могут отсутствовать верхние или нижние границы. Для примера:

Несмотря на отсутствие явных ограничений, существуют уровни, которые не могут быть достигнуты компонентами. Например, если один компонент представляет вес одного алмаза, существует неявная верхняя граница 1 кг (алмаз надежды меньше 10 г). В таком случае задайте неявную границу как верхнюю границу.
Здесь действительно нет верхней границы. Для примера размер файла компьютера в байтах не имеет эффективной верхней границы. Самый большой размер может быть в гигабайтах или терабайтах сегодня, но через 10 лет, кто знает?

Для действительно неограниченных компонентов можно использовать следующие методы дискретизации. Чтобы сгенерировать приблизительно 1/ n точек в каждой области (exp (n), exp (n + 1)), используйте следующую формулу. Если u случайен и равномерно распределен от 0 до 1, то r = 2 u - 1 равномерно распределена между -1 и 1. Бери

$y = sgn (r) (\exp (1 / | r |) - e) .$

y симметрично и случайно. Для переменной, ограниченной ниже lbБери

$y = lb + (\exp (1 / u) - e) .$

Точно так же для переменной, ограниченной выше ubБери

$y = ub - (\exp (1 / u) - e) .$

Например, предположим, что у вас есть трехмерная задача с

x(1) > 0
x(2) < 100
x(3) без ограничений

Чтобы сделать 150 начальных точек, удовлетворяющих этим ограничениям:

u = rand(150,3);
r1 = 1./u(:,1);
r1 = exp(r1) - exp(1);
r2 = 1./u(:,2);
r2 = -exp(r2) + exp(1) + 100;
r3 = 1./(2*u(:,3)-1);
r3 = sign(r3).*(exp(abs(r3)) - exp(1));
custpts = CustomStartPointSet([r1,r2,r3]);

Следующий вариант этого алгоритма. Сгенерируйте число от 0 до бесконечности методом для нижних границ. Используйте это число как радиус точки. Сгенерируйте другие компоненты точки путем взятия случайных чисел для каждого компонента и умножьте на радиус. Можно нормировать случайные числа, перед умножением на радиус, поэтому их норма равна 1. Для рабочего примера этого метода смотрите MultiStart без границ, Широко рассредоточенные стартовые точки.

Пример: Поиск лучшего решения

MultiStart не удается найти глобальный минимум в Multi Local Minima Via MultiStart. Существует два простых способа поиска лучшего решения:

Используйте больше начальных точек
Задайте более жесткие ограничения в пространстве поиска

Настройте структуру и MultiStart задачи объект:

problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Algorithm','quasi-newton'));
ms = MultiStart;

Используйте больше начальных точек

Выполняйте MultiStart о задаче на 200 стартовых точек вместо 50:

rng(14,'twister') % for reproducibility
[x,fval,eflag,output,manymins] = run(ms,problem,200)

MultiStart completed some of the runs from the start points.

53 out of 200 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-06 *

   -0.2284   -0.5567


fval =

   2.1382e-12


eflag =

     2


output = 

  struct with fields:

                funcCount: 32670
         localSolverTotal: 200
       localSolverSuccess: 53
    localSolverIncomplete: 147
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵53 out of 200 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x53 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
    X0

На этот раз MultiStart нашел глобальный минимум, и нашел 51 локальный минимум.

Чтобы увидеть область значений локальных решений, введите histogram([manymins.Fval],10).

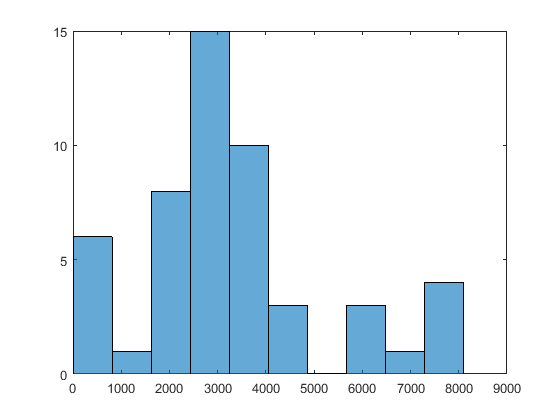
Более плотная граница начальных точек

Предположим, вы верите, что интересные локальные решения имеют абсолютные значения всех компонентов менее 100. Значение по умолчанию привязки начальных точек - 1000. Чтобы использовать другое значение границы, сгенерируйте RandomStartPointSet с ArtificialBound значение свойства установлено в 100:

startpts = RandomStartPointSet('ArtificialBound',100,...
    'NumStartPoints',50);
[x,fval,eflag,output,manymins] = run(ms,problem,startpts)

MultiStart completed some of the runs from the start points.

29 out of 50 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-08 *

    0.9725   -0.6198


fval =

   1.4955e-15


eflag =

     2


output = 

  struct with fields:

                funcCount: 7431
         localSolverTotal: 50
       localSolverSuccess: 29
    localSolverIncomplete: 21
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵29 out of 50 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x25 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
    X0

MultiStart нашел глобальный минимум и нашел 22 различных локальных решения. Чтобы увидеть область значений локальных решений, введите histogram([manymins.Fval],10).

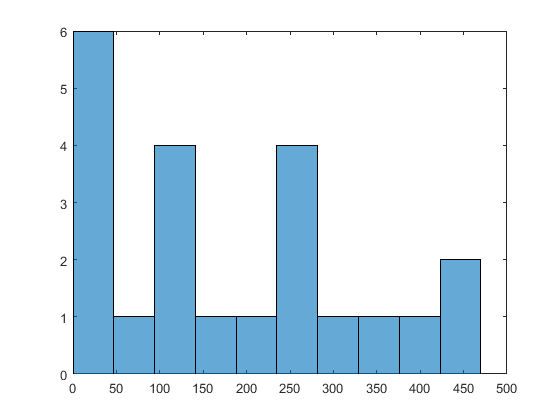
По сравнению с минимумами, найденными в Use More Start Points, этот запуск нашел лучшие (меньшие) минимумы и имел более высокий процент успешных запусков.

Документация