MATLAB® Пользовательский интерфейс Basic Fitting позволяет вам в интерактивном режиме:
Моделируйте данные с помощью сплайн интерполяции, кубической Эрмитовой интерполяции или полинома до десятой степени
Построение графика одной или несколькой подгонки с данными
Постройте график невязок подгонок
Вычислите коэффициенты модели
Вычислите норму невязок (статистика, которую вы можете использовать, чтобы проанализировать, насколько хорошо модель подходит для ваших данных)
Используйте модель для интерполяции или экстраполяции вне данных
Сохраните коэффициенты и вычисленные значения в рабочем пространстве MATLAB для использования вне диалогового окна
Сгенерируйте код MATLAB, чтобы пересчитать подгонку и воспроизвести графики с новыми данными
Примечание
Этот Пользовательский интерфейс Basic Fitting доступен только для 2-D графиков. Для получения дополнительной информации подбор кривой и регрессионном анализе смотрите документацию Curve Fitting Toolbox™ и документацию Statistics and Machine Learning Toolbox™.
Пользовательский интерфейс Basic Fitting сортирует ваши данные в порядке возрастания перед подбором кривой. Если ваш набор данных велик, и значения не сортируются в порядке возрастания, пользовательскому интерфейсу Basic Fitting требуется больше времени для предварительной обработки данных перед подбором кривой.
Вы можете ускорить пользовательский интерфейс Basic Fitting, предварительно отсортировав свои данные. Чтобы создать отсортированные векторы x_sorted и y_sorted из векторов данных x и y, используйте MATLAB sort функция:
[x_sorted, i] = sort(x); y_sorted = y(i);
Чтобы использовать Пользовательский Интерфейс Basic Fitting, необходимо сначала построить график данных в окне рисунка с помощью любой команды построения графического изображения MATLAB, которая производит (только) данные x и y.
Чтобы открыть пользовательский интерфейс Basic Fitting, выберите Tools > Basic Fitting из меню в верхней части окна рисунка.
В этом примере показано, как использовать Пользовательский Интерфейс Basic Fitting для подгонки, визуализации, анализа, сохранения и генерации кода для параболических регрессий.
Файл census.mat содержит население данные США за 1790-1990 годы по состоянию на 10 лет интервалов.
Чтобы загрузить и построить график данных, введите следующие команды в подсказку MATLAB:
load census plot(cdate,pop,'ro')
The load команда добавляет следующие переменные в рабочее пространство MATLAB:
cdate - вектор-столбец, содержащий годы с 1790 по 1990 годы с шагами 10. Это переменная предиктора.
pop - Вектор-столбец с населением в США для каждого года в cdate. Это переменная отклика.
Векторы данных сортируются в порядке возрастания по годам. График показывает население как функцию года.
Теперь вы готовы подогнать под уравнение данные для моделирования роста населения с течением времени.
Откройте диалоговое окно Basic Fitting, выбрав Tools > Basic Fitting в окне рисунка.
В области TYPES OF FIT диалогового окна Basic Fitting установите флажок Cubic, чтобы соответствовать кубическому полиному данных.
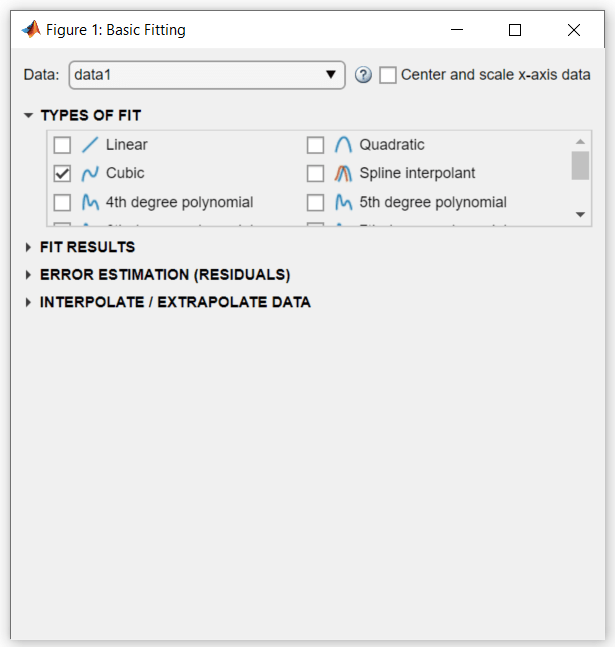
MATLAB использует ваш выбор, чтобы соответствовать данным, и добавляет кубическую регрессионую линию к графику следующим образом.
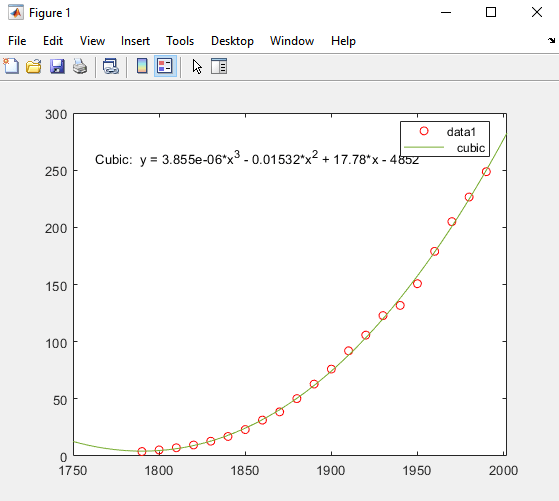
При вычислении подгонки MATLAB сталкивается с проблемами и выдает следующее предупреждение:
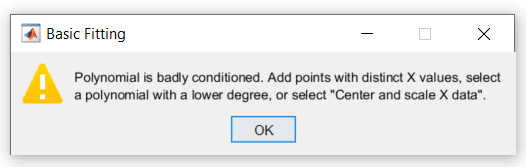
Это предупреждение указывает, что вычисленные коэффициенты для модели чувствительны к случайным ошибкам в отклике (измеренное население). Это также предполагает некоторые вещи, которые вы можете сделать, чтобы получить лучшую подгонку.
Продолжите использовать кубическое соответствие. Поскольку вы не можете добавить новые наблюдения к данным переписи, улучшите подгонку, преобразовав значения, которые у вас есть, в z-оценки перед пересчетом подгонки. Установите флажок Center and scale x-axis data в правом верхнем углу диалогового окна, чтобы инструмент Basic Fitting выполнил преобразование.
Чтобы узнать, как работает центрирование и масштабирование данных, см. Раздел «Изучение того, как вычисляет Basic Fitting Tool».
В разделе ERROR ESTIMATION (RESIDUALS) установите флажок Norm of residuals. Выберите Bar в качестве Plot Style.
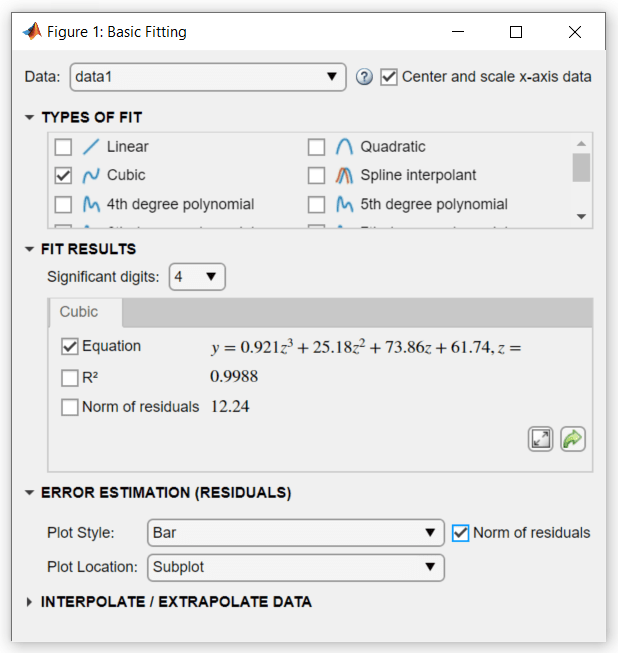
Выбор этих опций создает подграфик невязок как гистограмма.
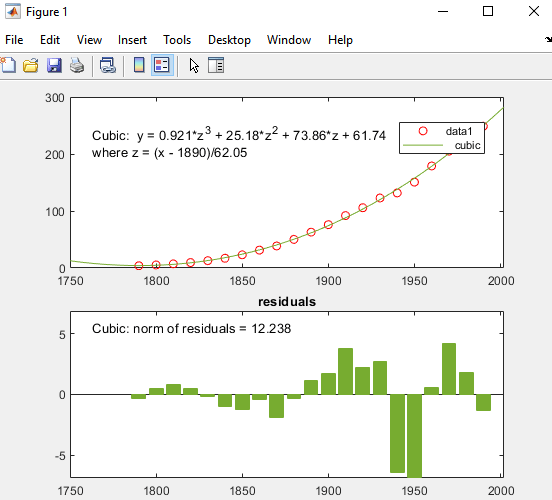
Кубическое соответствие является плохим предиктором до 1790 года, где она указывает на уменьшение населения. Модель, по-видимому, достаточно хорошо аппроксимирует данные после 1790 года. Однако шаблон в невязках показывает, что модель не соответствует предположению о нормальной ошибке, что является базисом для подбора кривой методом наименьших квадратов. Линией data 1, идентифицированной в легенде, являются наблюдаемые x (cdate) и y (pop) значения данных. Линия регрессии Cubic представляет подгонке после центрирования и масштабирования значений данных. Заметьте, что на рисунке показаны исходные модули данных, даже если инструмент вычисляет подгонку с помощью преобразованных z-значений.
Для сравнения попробуйте подгонять другое полиномиальное уравнение к данным переписи путем выбора его в области TYPES OF FIT.
В диалоговом окне Basic Fitting нажмите кнопку Expand Results![]() , чтобы отобразить предполагаемые коэффициенты и норму невязок.
, чтобы отобразить предполагаемые коэффициенты и норму невязок.
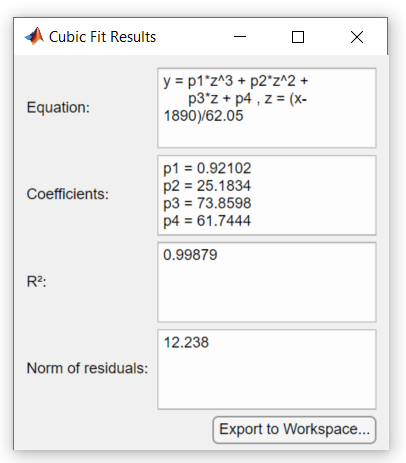
Сохраните данные подгонки в рабочем пространстве MATLAB, нажав кнопку Export to Workspace на панели Числовые результаты. Откроется диалоговое окно Сохранить подгонку в рабочей области (Save Fit to Workspace).
Если установлены все флажки, щелкните OK, чтобы сохранить параметры подгонки как структуру MATLAB fit:
fit
fit =
struct with fields:
type: 'polynomial degree 3'
coeff: [0.9210 25.1834 73.8598 61.7444]Теперь можно использовать результаты подгонки в программировании MATLAB, за пределами пользовательского интерфейса Basic Fitting.
Можно получить указание на то, насколько хорошо параболическая регрессия предсказывает ваши наблюдаемые данные путем вычисления coefficient of determination, или R-square (написано как R2). R2 statistic, которая находится в диапазоне от 0 до 1, измеряет, насколько полезна независимая переменная в предсказании значений зависимой переменной:
R2 значение около 0 указывает, что подгонка не намного лучше модели y = constant.
R2 значение около 1 указывает, что независимая переменная объясняет большую часть переменной в зависимой переменной.
R2 вычисляются из residuals, различия со знаком между наблюдаемым зависимым значением и значением, которое ваша подгонка предсказывает для него.
| невязки = yobserved - yited | (1) |
R2 номер для кубического соответствия в этом примере, 0.9988, расположен под FIT RESULTS в диалоговом окне Basic Fitting.
Для сравнения R2 число для кубического соответствия к линейному методу наименьших квадратов подгонке, выберите Linear под TYPES OF FIT и получите R2 число, 0,921. Этот результат указывает, что линейный метод наименьших квадратов данных о населении объясняет 92,1% своих отклонений. Поскольку кубическое соответствие этих данных объясняют 99,9% этого отклонения, последняя, по-видимому, является лучшим предиктором. Однако, потому что кубическое соответствие предсказывает использование трех переменных (x, x2, и x3), основной R2 значение не полностью отражает, насколько устойчива подгонка. Более подходящая мера для оценки качества многомерных соответствий скорректирована R2. Для получения информации об вычислениях и использовании скорректированных R2, см. Невязки и качество подгонки.
Предположим, что вы хотите использовать кубическую модель для интерполяции населения США в 1965 году (дата не указана в исходных данных).
В диалоговом окне «Basic Fitting» в разделе INTERPOLATE / EXTRAPOLATE DATA введите значение X 1965 и установите флажок Plot evaluated data.
Примечание
Используйте немасштабированные и uncentered X значения. Вам не нужно сначала центрировать и масштабировать, даже если вы выбрали для масштабирования X значения для получения коэффициентов в разделе Предсказание данных переписи населения с помощью кубической Аппроксимации полиномом. Инструмент Basic Fitting вносит необходимые корректировки за кадром.
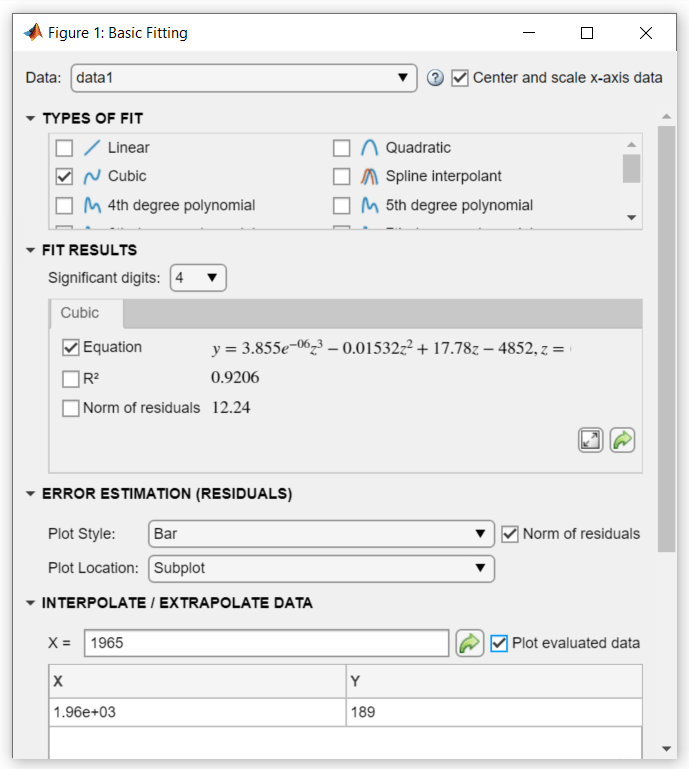
The X значений и соответствующих значений для f(X) вычисляются из подгонки и строятся следующим образом:
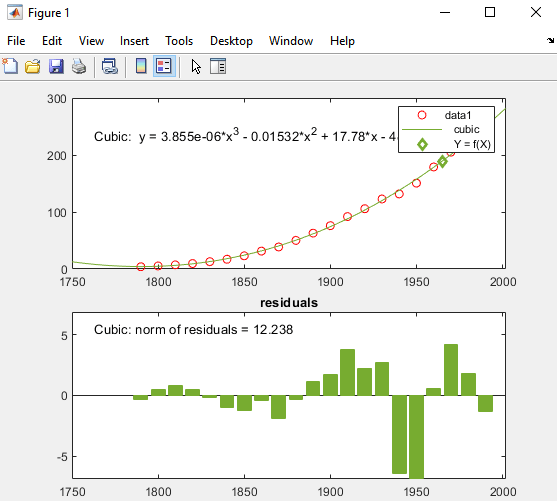
После завершения сеанса Basic Fitting можно сгенерировать код MATLAB, который пересчитывает подгонку и воспроизводит графики с новыми данными.
В окне рисунка выберите File > Generate Code.
Это создает функцию и отображает ее в редакторе MATLAB. Код показывает, как программно воспроизвести то, что вы сделали в интерактивном режиме с помощью диалогового окна Basic Fitting.
Измените имя функции в первой линии из createfigure к чему-то более конкретному, например censusplot. Сохраните файл кода в текущую папку с именем файла censusplot.m Функция начинается с:
function censusplot(X1, Y1, valuesToEvaluate1)
Сгенерируйте некоторые новые, случайным образом возмущенные данные переписи:
rng('default')
randpop = pop + 10*randn(size(pop));Воспроизведите график с новыми данными и пересчитайте подгонку:
censusplot(cdate,randpop,1965)
Вам нужно три входных параметров: x,y значения (data 1), нанесенный на исходный график, плюс x значение для маркера .
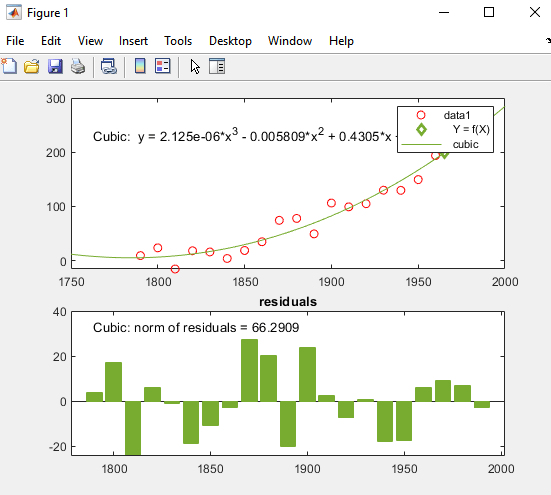
Следующий рисунок отображает график, который создает сгенерированный код. Новый график соответствует внешнему виду рисунка, из которых вы сгенерированными кодами, за исключением значений y данных, уравнения для кубического соответствия и невязки значений в гистограмму, как и ожидалось.
Инструмент Basic Fitting вызывает polyfit функция для вычисления аппроксимаций полиномом. Он вызывает polyval функция для оценки подгонок. polyfit анализирует его входы, чтобы определить, хорошо ли данные обусловлены требуемой степенью подгонки.
Когда он находит плохо обусловленные данные, polyfit вычисляет регрессию, а также может, но также возвращает предупреждение о том, что подгонка может быть улучшена. В Basic Fitting примере в разделе Предсказание данных переписи населения с помощью кубической Аппроксимации полиномом отображается это предупреждение.
Один из способов улучшить надежность модели - добавить точки данных. Однако добавление наблюдений к набору данных не всегда допустимо. Альтернативная стратегия состоит в том, чтобы преобразовать переменную предиктора, чтобы нормализовать ее центр и шкалу. (В примере предиктором является вектор дат переписи.)
polyfit функция нормализуется путем вычисления z-оценок:
где x - данные предиктора, μ - среднее значение x, а σ - стандартное отклонение x. Символы z-scores дают данным среднее значение 0 и стандартное отклонение 1. В пользовательском интерфейсе Basic Fitting вы преобразуете данные предиктора в z -счета, установив флажок Center and scale x-axis data.
После центрирования и масштабирования коэффициенты модели вычисляются для данных y как функция от z. Они отличаются (и более устойчивы) от коэффициентов, вычисленных для y как функции x. Форма модели и норма невязок не изменяются. Пользовательский интерфейс Basic Fitting автоматически пересматривает z -счета так, чтобы подгонка строилась в той же шкале, что и исходные данные x.
Чтобы понять, как центрированные и масштабированные данные используются в качестве посредника для создания окончательного графика, запустите следующий код в Командном окне:
close load census x = cdate; y = pop; z = (x-mean(x))/std(x); % Compute z-scores of x data plot(x,y,'ro') % Plot data as red markers hold on % Prepare axes to accept new graph on top zfit = linspace(z(1),z(end),100); pz = polyfit(z,y,3); % Compute conditioned fit yfit = polyval(pz,zfit); xfit = linspace(x(1),x(end),100); plot(xfit,yfit,'b-') % Plot conditioned fit vs. x data
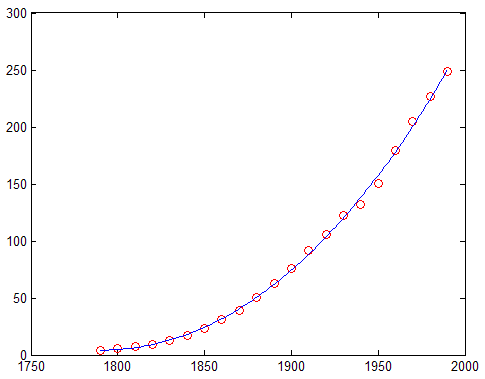
Центрированный и масштабированный кубический полином строит графики как синяя линия, как показано здесь:
В коде расчет z иллюстрирует, как нормализовать данные. polyfit функция выполняет само преобразование, если при вызове задаете три возвращаемых аргументов:
[p,S,mu] = polyfit(x,y,n)
p, теперь основаны на нормализованных x. Возвращенный вектор, mu, содержит среднее и стандартное отклонение x. Для получения дополнительной информации смотрите polyfit страница с описанием.