(Не рекомендуемый) Простой в использовании 3-D цветной поверхностный плоттер
ezsurf не рекомендуется. Использовать fsurf вместо этого.
ezsurf(fun)
ezsurf(fun,domain)
ezsurf(funx,funy,funz)
ezsurf(funx,funy,funz,[smin,smax,tmin,tmax])
ezsurf(funx,funy,funz,[min,max])
ezsurf(...,n)
ezsurf(...,'circ')
ezsurf(axes_handle,...)
h = ezsurf(...)
ezsurf(fun) создает графиков fun(x,y) использование surf функция. fun нанесено на график в области по умолчанию: -2, < x <2π,-2π <y < 2π.
fun может быть указателем на функцию, вектором символов или строкой (см. раздел Советов).
ezsurf(fun,domain) графики fun по заданному domain. domain должен быть вектором. Смотрите раздел Алгоритмы для получения дополнительной информации о векторных входах и предельных выходах осей.
ezsurf(funx,funy,funz) строит графики параметрической поверхности funx(s,t), funy(s,t), и funz(s,t) над квадратом: -2, < s <2π,-2π <t < 2π.
ezsurf(funx,funy,funz,[smin,smax,tmin,tmax]) или ezsurf(funx,funy,funz,[min,max]) строит графики параметрической поверхности с помощью заданной области.
ezsurf(...,n) графики fun по умолчанию область с использованием n-by- n сетка. Значение по умолчанию для n составляет 60.
ezsurf(...,'circ') графики fun по диску с центром в области.
ezsurf(axes_handle,...) графики в осях с указателем axes_handle вместо текущей системы координат (gca).
h = ezsurf(...) возвращает указатель на объект поверхности в h.
Постройте график функции над областью и . The ezsurf функция не строит график точек, где математическая функция не задана. Эти точки установлены в NaN чтобы они не строились.
figure
ezsurf('real(atan(x+i*y))')
Использование surf для построения графика тех же данных без фильтрации разрывов.
figure [x,y] = meshgrid(linspace(-2*pi,2*pi,60)); z = real(atan(x+1i.*y)); surf(x,y,z)
ezsurf и ezsurfc не принимайте комплексные входы.
Умножение, деление и экспоненция массива всегда подразумеваются в выражении, которое вы передаете ezsurf. Для примера, MATLAB® синтаксис для объемной поверхностной диаграммы выражения
sqrt(x.^2 + y.^2);
записывается как
ezsurf('sqrt(x^2 + y^2)')То есть x^2 интерпретируется как x.^2 в векторе символов или строке, в которую вы переходите ezsurf.
Если функция, которая будет нанесена на график, является функцией от переменных u и v (а не x и y), то доменные конечные точки umin, umax, vmin, и vmax сортируются в алфавитном порядке. Таким образом, ezsurf('u^2 - v^3',[0,1],[3,6]) графики u2 - v3 более 0 < u < 1, 3 < v < 6.
Аргументы указателя на функцию должны указывать на функции, которые используют синтаксис MATLAB. Например, следующие операторы определяют анонимную функцию и передают указатель на функцию fh на ezsurf.
fh = @(x,y) sqrt(x.^2 + y.^2); ezsurf(fh)
Обратите внимание, что при использовании указателей на функцию необходимо использовать степень массива, умножение массива и операторы деления массива (.^, .*, ./) с ezsurf не изменяет синтаксис, как в случае с вектором символов или строковыми входами.
Если ваша функция имеет дополнительные параметры, например k в myfun:
function z = myfun(x,y,k1,k2,k3) z = x.*(y.^k1)./(x.^k2 + y.^k3);
затем можно использовать анонимную функцию, чтобы задать этот параметр:
ezsurf(@(x,y)myfun(x,y,2,2,4))
ezsurf определяет пределы осей X и Y различными способами в зависимости от того, как вы вводите область (если вообще). В следующей таблице R - вектор [xmin, xmax, ymin, ymax] и v - вектор области, введенный вручную.
| Количество заданных областей значений: | Получившийся вектор области: |
|---|---|
v = [ ]; |
R = [-2*pi, 2*pi, -2*pi, 2*pi]; |
v = [ v(1) ]; |
R = double([-abs(v),abs(v),-abs(v),abs(v)]); |
v = [ v(1) v(2) ]; |
R = double([v(1),v(2),v(1),v(2)]); |
v = [ v(1) v(2) v(3) ]; |
R = double([-v(1),v(2),-abs(v(3)),abs(v(3))]); |
v = [ v(1) v(2) v(3) v(4) ]; |
R = double(v); |
v = [ v(1)..v(n) ]; n>4 |
R = double([-abs(v(1)), abs(v(1)), -abs(v(1)), abs(v(1))]); |
Если вы задаете одно число в невекторном формате (без квадратных скобок, []), ezsurf интерпретирует его как n, число точек, требуемая между осями max и min значения.
По умолчанию ezsurf использует 60 точек между max и min значения осей. Когда min и max значения являются значениями по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];), ezsurf обеспечивает попадание 60 точек в некомпонентную область значений заданного уравнения. Для примера, реально только тогда, когда . График по умолчанию этой функции выглядит следующим образом:
ezsurf('sqrt(1-x^2-y^2)')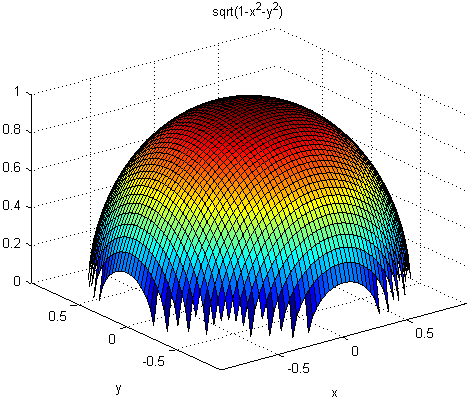
Вы можете увидеть, что существует 60 точек между минимальным и максимальным значениями, для которых имеет действительные значения. Однако, когда вы задаете, что значения области те же, что и по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];) появляется другой результат:
ezsurf('sqrt(1-x^2-y^2)',[-2*pi 2*pi])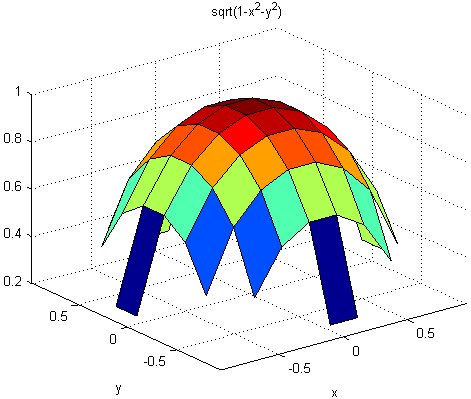
В этом случае графические пределы одинаковы, но ezsurf вместо проверки использовали 60 точек между определенными пользователем пределами, чтобы увидеть, будут ли все эти точки иметь реальные ответы.