Вы можете использовать sim для симуляции системы с обратной связью, состоящей из линейной модели объекта управления и контроллера MPC.
Если ваш объект является нелинейным Simulink® необходимо линеаризировать объект (см. Linearization Using Model Linearizer in Simulink Control Design) и разработать контроллер для линейной модели (см. Design MPC Controller in Simulink). Чтобы симулировать систему, укажите контроллер в поле MPC параметры блоков MPC Controller и запустите модель Simulink с обратной связью.
Кроме того, ваша нелинейная модель может быть файлом MEX, или вы можете захотеть включить функции, недоступные в блок MPC, например, пользовательский оценщик состояния. mpcmove функция является вычислительным механизмом Model Predictive Control Toolbox™, и вы можете использовать его в таких случаях. Недостатком является то, что вы должны дублировать инфраструктуру, которая sim функция и блок MPC обеспечивают автоматически.
The CSTR модель, описанная в Linearize Simulink Models, является сильно нелинейной системой. Как показано на Design MPC Controller в Simulink, контроллер может регулировать этот объект, но ухудшается (и может даже стать нестабильным), если рабочая точка значительно изменяется.
Цель этого примера состоит в том, чтобы переопределить прогнозирующий контроллер в начале каждого контрольного интервала, так что его прогнозирующая модель, хотя и линейная, представляет последние условия объекта как можно точнее. Это будет сделано путем повторной линеаризации нелинейной модели, что позволяет контроллеру адаптироваться по мере изменения условий объекта. Для получения дополнительной информации об этом подходе см. [1] и [2].
В следующем коде симуляция начинается в номинальной рабочей точке CSTR модель (концентрация = 8,57) и переходит к нижней точке (концентрация = 2), где скорость реакции намного выше. Необходимый код следующий:
[sys, xp] = CSTR_INOUT([],[],[],'sizes'); up = [10 298.15 298.15]; u = up(3); tsave = []; usave = []; ysave = []; rsave = []; Ts = 1; t = 0; while t < 40 yp = xp; % Linearize the plant model at the current conditions [a,b,c,d] = linmod('CSTR_INOUT',xp,up); Plant = ss(a,b,c,d); Plant.InputGroup.ManipulatedVariables = 3; Plant.InputGroup.UnmeasuredDisturbances = [1 2]; Model.Plant = Plant; % Set nominal conditions to the latest values Model.Nominal.U = [0 0 u]; Model.Nominal.X = xp; Model.Nominal.Y = yp; dt = 0.001; simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+dt); simOptions.LoadInitialState = 'on'; simOptions.InitialState = 'xp'; simOptions.SaveTime = 'on'; simOptions.SaveState = 'on'; simOptions.LoadExternalInput = 'on'; simOptions.ExternalInput = '[t up; t+dt up]'; simOut = sim('CSTR_INOUT',simOptions); T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); Model.Nominal.DX = (1/dt)*(XP(end,:)' - xp(:)); % Define MPC controller for the latest model MPCobj = mpc(Model, Ts); MPCobj.W.Output = [0 1]; % Ramp the setpoint r = max([8.57 - 0.25*t, 2]); % Compute the control action if t <= 0 xd = [0; 0]; x = mpcstate(MPCobj,xp,xd,[],u); end u = mpcmove(MPCobj,x,yp,[0 r],[]); % Simulate the plant for one control interval up(3) = u; simOptions.StartTime = num2str(t); simOptions.StopTime = num2str(t+Ts); simOptions.InitialState = 'xp'; simOptions.ExternalInput = '[t up; t+Ts up]'; simOut = sim('CSTR_INOUT',simOptions); T = simOut.get('tout'); XP = simOut.get('xout'); YP = simOut.get('yout'); % Save results for plotting tsave = [tsave; T]; ysave = [ysave; YP]; usave = [usave; up(ones(length(T),1),:)]; rsave = [rsave; r(ones(length(T),1),:)]; xp = XP(end,:)'; t = t + Ts; end figure(1) plot(tsave,[ysave(:,2) rsave]) title('Residual Concentration') figure(2) plot(tsave,usave(:,3)) title('Coolant Temperature')
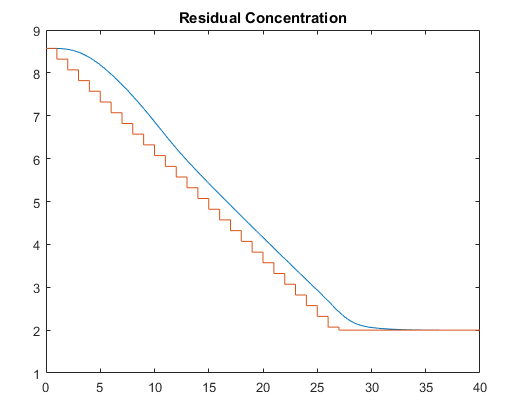
Нанесенные на график результаты показаны ниже. Обратите внимание на следующие точки:
Уставка растёт от начальной концентрации до желаемого конечного значения (см. ступенчатые изменения на графике концентрации реактора ниже). Концентрация реактора отслеживает этот перепад плавно с некоторой задержкой (см. гладкую кривую) и оседает в конечном состоянии с незначительным перерегулированием. Контроллер работает одинаково хорошо (и быстрее достигает конечной концентрации) для поэтапного изменения уставки, но он производит нереально быстрые изменения температуры хладагента (не показан).
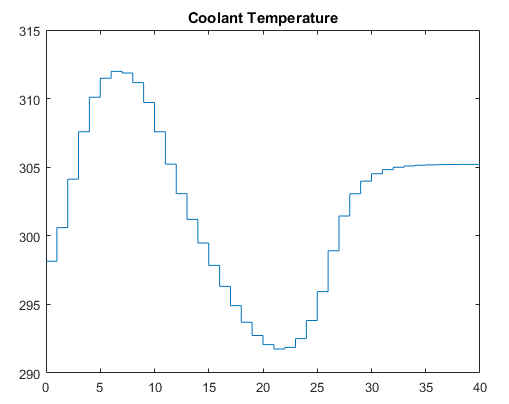
Конечное установившееся состояние требует температуры хладагента 305,20 К (см. график температуры хладагента ниже). Интересной функцией этого нелинейного объекта является то, что если начать в исходном установившемся состоянии (температура хладагента = 298,15 К), то ступень температуры хладагента до 305,20 и выдержка не достигнут желаемой конечной концентрации 2. Фактически, при такой простой стратегии концентрация в реакторе стабилизируется при конечном значении 7,88, далеком от желаемого значения. Успешный контроллер должен увеличить температуру реактора до тех пор, пока реакция не «не взлетит», после чего он должен снизить температуру хладагента, чтобы справиться с повышенной тепловой нагрузкой. Подход релинеаризации обеспечивает такой контроллер (см. следующие графики).
Функция linearize расслабляет объект по мере развития его состояния. Эта функция обсуждалась ранее в Linearization Using MATLAB Code.
Код также сбрасывает номинальные условия линейной модели к последним значениям. Обратите внимание, однако, что первые два входных сигналов, которые являются неизмеренными нарушениями порядка в проектировании контроллера, всегда имеют номинальные нулевые значения. Поскольку они не измерены, контроллер не может быть проинформирован об истинных значениях. Ненулевое значение приведет к ошибке.
Функция mpc задает новый контроллер на основе релинеаризированной модели объекта управления. Настройка выходного веса игнорирует измерение температуры, фокусируясь только на концентрации.
При t = 0, mpcstate функция инициализирует расширенный вектор состояния контроллера, x. После этого mpcmove функция автоматически обновляет его с помощью оценки состояния контроллера по умолчанию. Также можно было бы использовать расширенный фильтр Калмана (EKF), как описано в [1] и [2], в этом случае EKF сбросит mpcstate входные переменные на каждом шаге.
mpcmove функция использует последнее определение и состояние контроллера, измеренные выходы объекта и уставки, чтобы вычислить новую температуру хладагента на каждом шаге.
Simulink sim Функция моделирует нелинейный объект от начала до конца контрольного интервала. Окончательное условие с предыдущего шага используется в качестве начального состояния объекта управления и что входы объекта остаются постоянными в течение каждого интервала.
Помните, что обычный контроллер обратной связи или фиксированный контроллер Model Predictive Control Toolbox, настроенный на работу в начальном состоянии, станет нестабильным, когда объект перейдет к конечному условию. Периодическое обновление модели автоматически преодолевает эту проблему и обеспечивает отличное управление при всех условиях.
[1] Lee, J. H. and N. L. Ricker, «Extended Kalman Filter Based Nonlinear Model Predictive Control», Ind. Eng. Chem. Res., Vol. 33, No 6, pp. 1530-1541 (1994).
[2] Ricker, N. L., and J. H. Lee «Nonlinear Model Predictive Control of the Tennessee Eastman Challenge Process», Computers & Chemical Engineering, Vol. 19, No. 9, pp. 961-981 (1995).