ecompass

Ориентация от показаний магнитометра и акселерометра

Синтаксис

orientation = ecompass(accelerometerReading,magnetometerReading)

orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat)

orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat,'ReferenceFrame',RF)

Описание

orientation = ecompass(accelerometerReading,magnetometerReading) возвращает quaternion который может вращать величины из родительской (NED) системы координат в дочернюю (sensor) систему координат.

пример

orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat) задает формат ориентации следующим quaternion или матрица вращения.

orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat,'ReferenceFrame',RF) также позволяет вам задать систему координат RF от orientation выход. Задайте RF как 'NED' (Северо-Восток-Даун) или 'ENU' (Восток-Север-Вверх). Значение по умолчанию 'NED'.

Примеры

свернуть все

Определите склонение Бостона

Открыть Live Script

Используйте известную напряженность магнитного поля и правильное ускорение устройства, указывающего истинный север в Бостоне, чтобы определить магнитное склонение Бостона.

Определите известное ускорение и напряженность магнитного поля в Бостоне.

magneticFieldStrength = [19.535 -5.109 47.930];
properAcceleration = [0 0 9.8];

Передайте напряженность и ускорение магнитного поля в ecompass функция. The ecompass функция возвращает оператор поворота кватерниона. Преобразуйте кватернион в углы Эйлера в степенях.

q = ecompass(properAcceleration,magneticFieldStrength);
e = eulerd(q,'ZYX','frame');

Угол, e, представляет угол между истинным севером и магнитным севером в Бостоне. По соглашению магнитное склонение отрицательно, когда магнитный север к западу от истинного севера. Отрицайте угол, чтобы определить магнитное склонение.

magneticDeclinationOfBoston = -e(1)

magneticDeclinationOfBoston = -14.6563

Матрица вращения возврата

Открыть Live Script

The ecompass функция преобразует данные магнитометра и акселерометра, чтобы вернуть кватернион, который при использовании в операторе вращения кватерниона может вращать величины из родительской (NED) системы координат в дочернюю систему координат. The ecompass функция может также возвращать матрицы вращения, которые выполняют эквивалентные повороты в качестве оператора.

Задайте вращение, которое может взять родительскую систему координат, указывающую на магнитный север, к дочерней системе координат, указывающей на географический север. Задайте вращение как кватернион и матрицу поворота. Затем преобразуйте кватернион и матрицу поворота в углы Эйлера в степенях для сравнения.

Определите напряженность магнитного поля в микротеслах в Бостоне, MA, когда указан истинный север.

m = [19.535 -5.109 47.930];
a = [0 0 9.8];

Определите кватернион и матрицу вращения, которая способна вращать систему координат с магнитного севера на истинный север. Отобразите результаты для сравнения.

q = ecompass(a,m);
quaterionEulerAngles = eulerd(q,'ZYX','frame')

quaterionEulerAngles = 1×3

   14.6563         0         0

r = ecompass(a,m,'rotmat');
theta = -asin(r(1,3));
psi = atan2(r(2,3)/cos(theta),r(3,3)/cos(theta));
rho = atan2(r(1,2)/cos(theta),r(1,1)/cos(theta));
rotmatEulerAngles = rad2deg([rho,theta,psi])

rotmatEulerAngles = 1×3

   14.6563         0         0

Определите вектор силы тяжести

Открыть Live Script

Использование ecompass для определения вектора силы тяжести на основе данных вращающегося БИНС.

Загрузите данные инерциального измерительного блока (IMU).

load 'rpy_9axis.mat' sensorData Fs

Определите ориентацию тела датчика относительно локальной системы координат NED с течением времени.

orientation = ecompass(sensorData.Acceleration,sensorData.MagneticField);

Чтобы оценить вектор тяжести, сначала поверните показания акселерометра из каркаса кузова датчика в систему координат NED с помощью orientation вектор кватерниона.

gravityVectors = rotatepoint(orientation,sensorData.Acceleration);

Определите вектор гравитации как среднее значение восстановленных векторов гравитации с течением времени.

gravityVectorEstimate = mean(gravityVectors,1)

gravityVectorEstimate = 1×3

    0.0000   -0.0000   10.2102

Платформа для прядения треков

Открыть Live Script

Смоделированные данные акселерометра и гироскопа предохранителя для отслеживания вращающейся платформы с помощью как идеализированных, так и реалистичных данных.

Сгенерируйте траекторию Основная истина

Опишите основную истину ориентацию платформы с течением времени. Используйте kinematicTrajectory Система object™, чтобы создать траекторию для платформы, которая не имеет никакого перемещения и вращается вокруг своей оси z.

duration = 12;
fs = 100;
numSamples = fs*duration;

accelerationBody = zeros(numSamples,3);

angularVelocityBody = zeros(numSamples,3);
zAxisAngularVelocity = [linspace(0,4*pi,4*fs),4*pi*ones(1,4*fs),linspace(4*pi,0,4*fs)]';
angularVelocityBody(:,3) = zAxisAngularVelocity;

trajectory = kinematicTrajectory('SampleRate',fs);

[~,orientationNED,~,accelerationNED,angularVelocityNED] = trajectory(accelerationBody,angularVelocityBody);

Модель приема данных БИНС

Использование imuSensor Системный объект для имитации данных, полученных от БИНС, который содержит идеальный магнитометр и идеальный акселерометр.

IMU = imuSensor('accel-mag','SampleRate',fs);
[accelerometerData,magnetometerData] = IMU(accelerationNED, ...
                                           angularVelocityNED, ...
                                           orientationNED);

Предохраните данные БИНС для оценки ориентации

Передайте данные о акселерометре и данные о магнитометре в ecompass функция для оценки ориентации с течением времени. Преобразуйте ориентацию в углы Эйлера в степенях и постройте график результата.

orientation = ecompass(accelerometerData,magnetometerData);
orientationEuler = eulerd(orientation,'ZYX','frame');

timeVector = (0:numSamples-1).'/fs;

figure(1)
plot(timeVector,orientationEuler)
legend('z-axis','y-axis','x-axis')
xlabel('Time (s)')
ylabel('Rotation (degrees)')
title('Orientation from Ideal IMU')

Figure contains an axes. The axes with title Orientation from Ideal IMU contains 3 objects of type line. These objects represent z-axis, y-axis, x-axis.

Повторите эксперимент с реалистичной моделью датчика IMU

Измените параметры IMU Системный объект для аппроксимации реалистичных данных о датчике БИНС. Сбросьте IMU и затем вызывайте его с тем же ускорением «земля-правда», скоростью вращения и ориентацией. Использование ecompass чтобы сплавить данные БИНС и построить график результатов.

IMU.Accelerometer = accelparams( ...
    'MeasurementRange',20, ...
    'Resolution',0.0006, ...
    'ConstantBias',0.5, ...
    'AxesMisalignment',2, ...
    'NoiseDensity',0.004, ...
    'BiasInstability',0.5);
IMU.Magnetometer = magparams( ...
    'MeasurementRange',200, ...
    'Resolution',0.01);
reset(IMU)

[accelerometerData,magnetometerData] = IMU(accelerationNED,angularVelocityNED,orientationNED);

orientation = ecompass(accelerometerData,magnetometerData);
orientationEuler = eulerd(orientation,'ZYX','frame');

figure(2)
plot(timeVector,orientationEuler)
legend('z-axis','y-axis','x-axis')
xlabel('Time (s)')
ylabel('Rotation (degrees)')
title('Orientation from Realistic IMU')

Figure contains an axes. The axes with title Orientation from Realistic IMU contains 3 objects of type line. These objects represent z-axis, y-axis, x-axis.

Входные параметры

свернуть все

`accelerometerReading` - Показания акселерометра в системе координат тела датчика (м/с²)
N -by-3 матрица

Показания акселерометра в системе координат тела датчика в м/с², заданный как матрица N -by-3. Столбцы матрицы соответствуют x -, y - и z - осям тела датчика. Строки в матрице, N, соответствуют отдельным выборкам. Показания акселерометра нормированы перед использованием в функции.

Типы данных: single | double

`magnetometerReading` - Показания магнитометра в системе координат тела датчика (мкТ)
N -by-3 матрица

Показания магнитометра в системе координат тела датчика в мкТ, заданные как матрица N-на-3. Столбцы матрицы соответствуют x -, y - и z - осям тела датчика. Строки в матрице, N, соответствуют отдельным выборкам. Показания магнитометра нормированы перед использованием в функции.

Типы данных: single | double

`orientationFormat` - Формат, используемый для описания ориентации
`'quaternion'` (по умолчанию) | `'rotmat'`

Формат, используемый для описания ориентации, задается как 'quaternion' или 'rotmat'.

Типы данных: char | string

Выходные аргументы

свернуть все

`orientation` - Ориентация, которая вращает величины от глобальной системы координат к системе координат тела датчика
N вектор кватернионов -by-1 (по умолчанию) | массив 3by-3-by- N

Ориентация, которая может поворачивать величины из глобальной системы координат в систему координат тела, возвращаемую как вектор кватернионов или массива. Размер и тип orientation зависит от формата, используемого для описания ориентации:

'quaternion' - N вектор кватернионов -by-1 с таким же базовым типом данных, как и вход
'rotmat' -- 3х3-бай- N массив совпадающего типа данных как вход

Типы данных: quaternion | single | double

Алгоритмы

ecompass функция возвращает кватернион или матрицу вращения, которая может вращать величины от родительского элемента (NED для примера) система координат к дочернему (датчику) система координат. Для обоих выходов форматов ориентации оператор поворота определяется вычислением матрицы поворота.

Матрица вращения сначала вычисляется с помощью посредника:

$R = [\begin{matrix} (a \times m) \times a & a \times m & a \end{matrix}]$

а затем нормированный столбчатый. a и m являются accelerometerReading вход и magnetometerReading вход, соответственно.

Чтобы понять вычисление матрицы вращения, рассмотрите произвольную точку на Земле и ее соответствующая локальная система координат. Предположим, что каркас кузова датчика [x, y, z] с тем же источником.

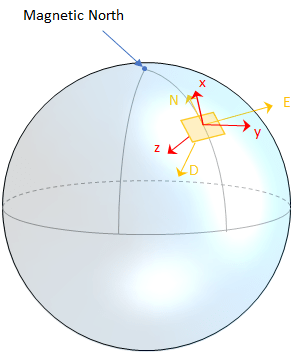
Напомним, что ориентация тела датчика определяется как оператор вращения (матрица вращения или кватернион), необходимый для поворота величины из родительской (NED) системы координат в дочернюю (тело датчика) систему координат:

$[\begin{matrix} R \end{matrix}] [\begin{matrix} p_{parent} \end{matrix}] = [\begin{matrix} p_{child} \end{matrix}]$

где

R - матрица вращения 3 на 3, которая может быть интерпретирована как ориентация дочерней системы координат.
p _{родительский элемент} является вектором 3 на 1 в родительской системе координат.
p _{дочерний элемент} является вектором 3 на 1 в дочерней системе координат.

Для стабильного тела датчика акселерометр возвращает ускорение за счет силы тяжести. Если тело датчика идеально выровнено с системой координат NED, все ускорения из-за силы тяжести расположены вдоль оси z, и акселерометр читает [0 0 1]. Рассмотрим матрицу поворота, необходимую для поворота величины из системы координат NED в величину, указанную акселерометром.

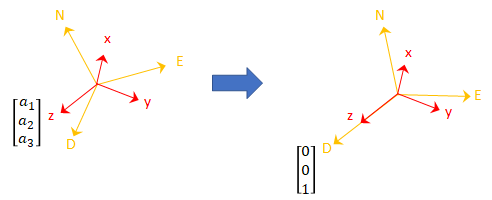
$[\begin{matrix} r_{11} & r_{21} & r_{31} \\ r_{12} & r_{22} & r_{32} \\ r_{13} & r_{23} & r_{33} \end{matrix}] [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] = [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}]$

Третий столбец матрицы вращения соответствует показанию акселерометра:

$[\begin{matrix} r_{31} \\ r_{32} \\ r_{33} \end{matrix}] = [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}]$

Показания магнитометра указывают на магнитный север и находятся в плоскости N - D. Снова рассмотрим каркас кузова датчика, выровненную с системой координат NED.

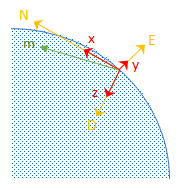
По определению E - ось перпендикулярна N - D самолет, поэтому <reservedrangesplaceholder7> ⨯ <reservedrangesplaceholder6> = E, в рамках некоторого амплитудного масштабирования. Если каркас кузова датчика выровнен с NED, вектор ускорения от акселерометра и вектор магнитного поля от магнитометра лежат в плоскости N - D. Поэтому m ⨯ a = y, снова с некоторым амплитудным масштабированием.

Рассмотрим матрицу вращения, необходимую для поворота NED в дочернюю систему координат [x y z].

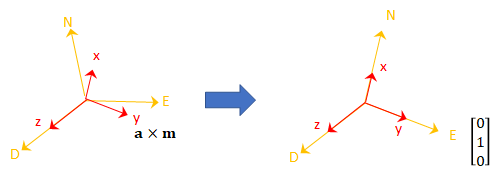
$[\begin{matrix} r_{11} & r_{21} & r_{31} \\ r_{12} & r_{22} & r_{32} \\ r_{13} & r_{23} & r_{33} \end{matrix}] [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}] = [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}] \times [\begin{matrix} m_{1} \\ m_{2} \\ m_{3} \end{matrix}]$

Второй столбец матрицы вращения соответствует перекрестному продукту показания акселерометра и показанию магнитометра:

$[\begin{matrix} r_{21} \\ r_{22} \\ r_{23} \end{matrix}] = [\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}] \times [\begin{matrix} m_{1} \\ m_{2} \\ m_{3} \end{matrix}]$

По определению матрицы поворота столбец 1 является перекрестным продуктом столбцов 2 и 3:

$\begin{array}{l} [\begin{matrix} r_{11} \\ r_{12} \\ r_{13} \end{matrix}] = [\begin{matrix} r_{21} \\ r_{22} \\ r_{23} \end{matrix}] \times [\begin{matrix} r_{31} \\ r_{32} \\ r_{33} \end{matrix}] \\ = (a \times m) \times a \end{array}$

Наконец, матрица вращения нормирована по столбцам:

$R_{i j} = \frac{R_{i j}}{\sqrt{\sum_{i = 1}^{3} R_{i j}^{2}}}, \forall j$

Примечание

ecompass алгоритм использует магнитный север, а не истинный север для системы координат NED.

Ссылки

[1] Комплексирование датчиков с открытым исходным кодом. https://github.com/memsindustrygroup/Open-Source-Sensor-Fusion/tree/master/docs

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

ahrsfilter | imufilter

Введенный в R2018b

Документация

ecompass

Синтаксис

Описание

Примеры

Определите склонение Бостона

Матрица вращения возврата

Определите вектор силы тяжести

Платформа для прядения треков

Входные параметры

`accelerometerReading` - Показания акселерометра в системе координат тела датчика (м/с²)
N -by-3 матрица

`magnetometerReading` - Показания магнитометра в системе координат тела датчика (мкТ)
N -by-3 матрица

`orientationFormat` - Формат, используемый для описания ориентации
`'quaternion'` (по умолчанию) | `'rotmat'`

Выходные аргументы

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

Документация по Navigation Toolbox

Поддержка

Документация

ecompass

Синтаксис

Описание

Примеры

Определите склонение Бостона

Матрица вращения возврата

Определите вектор силы тяжести

Платформа для прядения треков

Входные параметры

accelerometerReading - Показания акселерометра в системе координат тела датчика (м/с2) N -by-3 матрица

magnetometerReading - Показания магнитометра в системе координат тела датчика (мкТ) N -by-3 матрица

orientationFormat - Формат, используемый для описания ориентации 'quaternion' (по умолчанию) | 'rotmat'

Выходные аргументы

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

Документация по Navigation Toolbox

Поддержка

`accelerometerReading` - Показания акселерометра в системе координат тела датчика (м/с²)
N -by-3 матрица

`magnetometerReading` - Показания магнитометра в системе координат тела датчика (мкТ)
N -by-3 матрица

`orientationFormat` - Формат, используемый для описания ориентации
`'quaternion'` (по умолчанию) | `'rotmat'`

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®